particles of masses 2M m and M are resectively at points A , B and C with AB=12(BC) m is much - much smaller than M and at time t=0 they are all at rest as given in figure . As subsequent times before any collision takes palce .
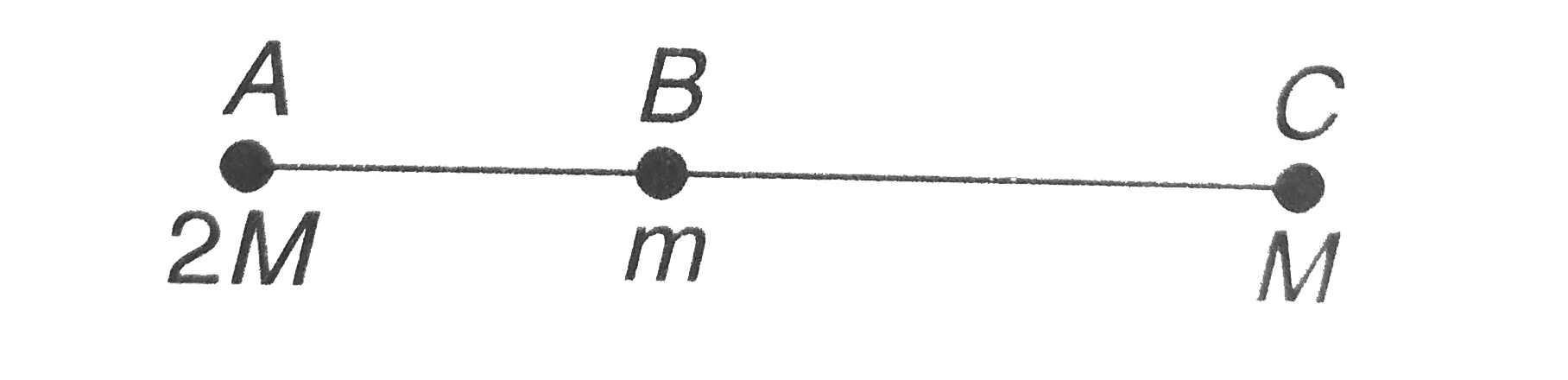
m will remain at rest
m will move towards M
m will move towards 2M
m will have oscillatory motion
The correct Answer is:C
Force on B due to A=FBA=G(2Mm)(AB)2 towards BA
Force on B due to C=FBC=GMm(BC)2 towards BC
As, (BC)=2AB
⇒FBC=GMm(2AB)2=GMm4(AB)2≤FBA
Hence, m will move towards BA (i.e., 2M)
Topper's Solved these Questions
- GRAVITATIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - GRAVITATIONEXERCISE - Very short Answer type question
11 Videos
- GRAVITATIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - GRAVITATIONEXERCISE - Short Answer type question
6 Videos
- KINETIC THEORYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Multiple Choice Questions (MCQs)
31 Videos
Similar Questions
Particles of masses 2M, m and M are respectively at points A, B and C with √GMR(√2+1) is much-much smaller than M and at time t=0, they are all at rest as given in figure
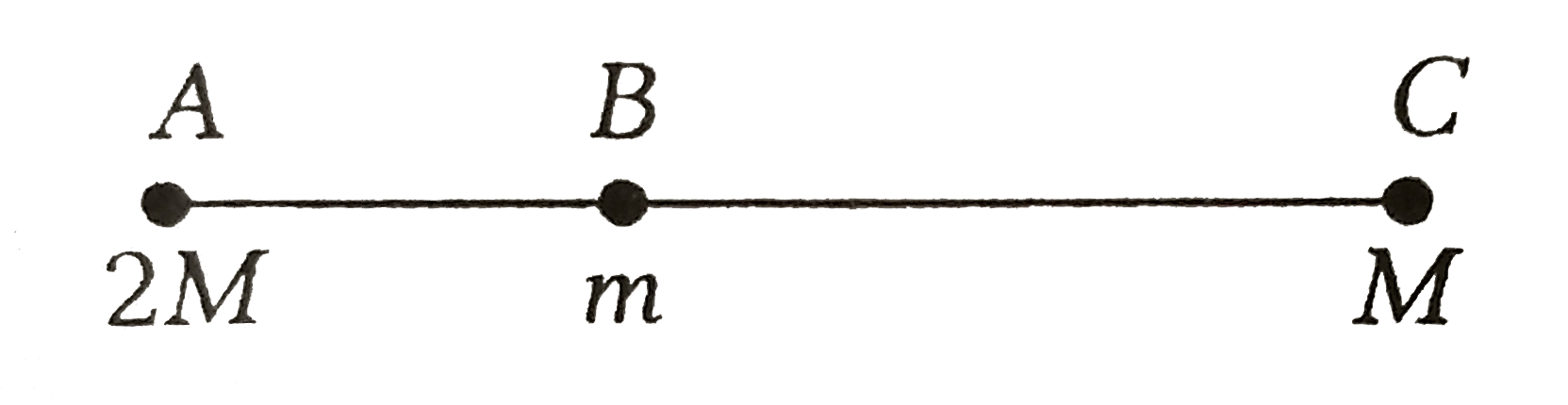
At subsequent time before any collision takes place.
View SolutionTwo particle of masses m and 2m are coliding elastically as given in figure. If V1 and V2 speed of particle just after collision then
_2019_CBT5_E01_051_Q01.png)
View SolutionA particle A of mass m initially at rest slides down a height of 1.25 m on a frictionless ramp, collides with and sticks to an identical particles B of mass m at rest as shown in the figure.

Then, particles A and B together collide elastically with particle G of mass 2m at rest. The speed of particle G after the collision with combined body (A+B) would be (Take, g=10ms−2)
View Solutionconsider a head on collision between two particles of masses m1andm2. The initial speeds of the particles are u1andu2 in the same direction. The collision starts at t=0 and the particles interact for a time interval △t. during the collision the speed of the first particle varies as
v(t)=u1+t/ t(v1−u1) Find the speed of the second particle as as function of time during the collision.
View SolutionTwo particles of masses m1 and m2 and velocities u1 and αu1(α≠0) make an elastic head on collision. If the initial kinetic energies of the two particles are equal and m1 comes to rest after collision, then
View SolutionTwo blocks A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a spring. A third block C of mass m moves with a velocity v0 along the line joing A and B and collides elastically with A, as shown in figure. At a certain instant of time t0 after collision, it is found that the instantaneous velocities of A and B are the same. Further, at this instant the compression of the spring is found to be x0. Determine (i) the common velocity of A and B at time t0, and (ii) the spring constant.
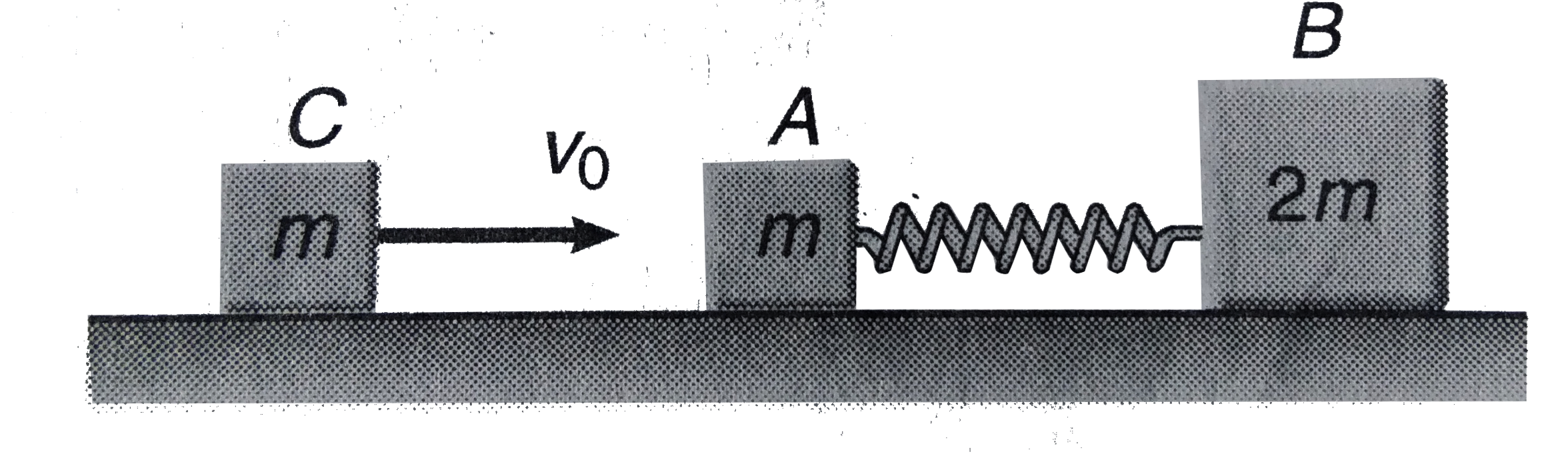
View SolutionA particle of mass m collides elastically with the pan of mass (M = 2m) of a spring balance, as shown in figure. Pan is in equillibrium before collision. Spring constant is k and speed of the particle before collision is v0 . Answer the following three questions regarding this collision.
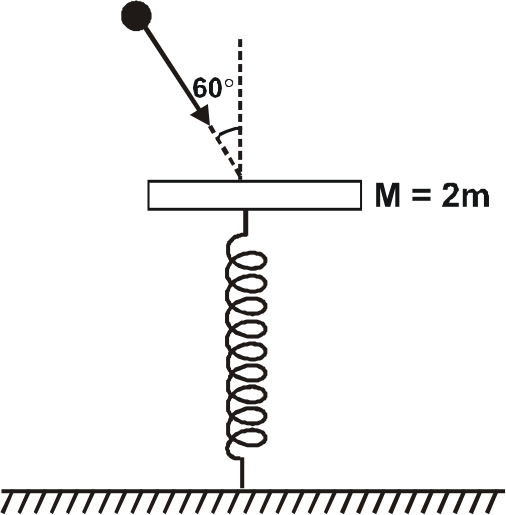
Minimum kinetic energy of the particle after collision is
View SolutionAt time t=0, a particle is at (−1m,2m) and at t=2s it is at (−4m,6m). From this we can conclude that in the given time interval.
View SolutionA particle of mass m collides elastically with the pan of mass (M = 2m) of a spring balance, as shown in figure. Pan is in equillibrium before collision. Spring constant is k and speed of the particle before collision is v0 . Answer the following three questions regarding this collision.
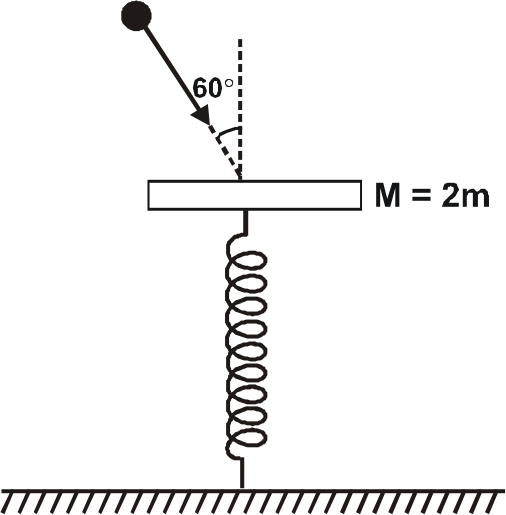
Maximum compression in the spring after the collision the
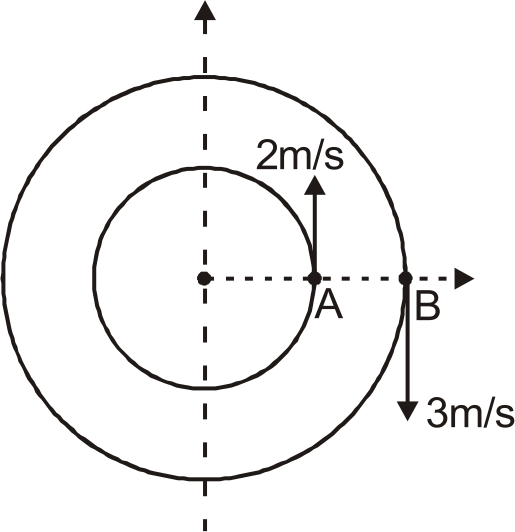
View SolutionTwo particles A and B are revolving with constant angular velocity on two concentric circles of radius 1m and 2m respectively as shown in figure. The positions of the particles at t = 0 are shown in figure. The positions of the particles at t=0 are shown in figure. if mA=2kg,mB=1kg and →PA and →PB are linear momentum of the particle then what is the maximum value of ∣∣→PA+→PB∣∣ in kg-m/sec in subsequent motion of two particles.
View Solution
