Passage XI) The differential equation of a particle undergoing SHM is given by ad2xdt2+bx = 0. The particle starts from the extreme position.
The ratio of the maximum acceleration to the maximum velocity of the particle is
b/a
a/b
√ab
√ba
The correct Answer is:D
To solve the problem, we need to analyze the given differential equation of a particle undergoing Simple Harmonic Motion (SHM) and derive the required ratio of maximum acceleration to maximum velocity.
1. Understand the Differential Equation:
The differential equation given is:
ad2xdt2+bx=0
This represents the motion of a particle in SHM.
2. Rearranging the Equation:
We can rearrange the equation to express the acceleration:
ad2xdt2=−bx
Dividing both sides by a:
d2xdt2=−bax
3. Identifying the Angular Frequency:
The standard form of SHM is:
d2xdt2=−ω2x
By comparing both equations, we can identify:
ω2=ba
Therefore, the angular frequency ω is:
ω=√ba
4. Maximum Acceleration and Maximum Velocity:
- The maximum acceleration Amax in SHM is given by:
Amax=ω2A
- The maximum velocity Vmax in SHM is given by:
Vmax=ωA
5. Finding the Ratio:
We need to find the ratio of maximum acceleration to maximum velocity:
AmaxVmax=ω2AωA
Simplifying this gives:
AmaxVmax=ω2ω=ω
6. Substituting the Value of ω:
From our earlier calculation, we have:
ω=√ba
Thus, the ratio of maximum acceleration to maximum velocity is:
AmaxVmax=√ba
Final Answer:
The ratio of the maximum acceleration to the maximum velocity of the particle is:
√ba
The differential equation given is:
ad2xdt2+bx=0
This represents the motion of a particle in SHM.
We can rearrange the equation to express the acceleration:
ad2xdt2=−bx
Dividing both sides by a:
d2xdt2=−bax
The standard form of SHM is:
d2xdt2=−ω2x
By comparing both equations, we can identify:
ω2=ba
Therefore, the angular frequency ω is:
ω=√ba
- The maximum acceleration Amax in SHM is given by:
Amax=ω2A
- The maximum velocity Vmax in SHM is given by:
Vmax=ωA
We need to find the ratio of maximum acceleration to maximum velocity:
AmaxVmax=ω2AωA
Simplifying this gives:
AmaxVmax=ω2ω=ω
From our earlier calculation, we have:
ω=√ba
Thus, the ratio of maximum acceleration to maximum velocity is:
AmaxVmax=√ba
The ratio of the maximum acceleration to the maximum velocity of the particle is:
√ba
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension types
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Matrix matching type questions
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Advanced
34 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Passage XI) The differential equation of a particle undergoing SHM is given by ad2xdt2+bx = 0. The particle starts from the extreme position.
The time period of osciallation is given by
View SolutionFor a particle in S.H.M. if the maximum acceleration is a and maximum velocity is v then amplitude is
View Solution
Knowledge Check
A particle executing simple harmonic motion with an amplitude A and angularr frequency ω. The ratio of maximum acceleration to the maximum velocity of the particle is
AωABω2ACωDω2A
A particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionA particle starts from rest with constant acceleration. The ratio of space-average velocity to the time average velocity is :-
View SolutionFor a particle performing SHM, equation of motion is given as d2dt2+9x=0. Find the time period
View SolutionFor a particle performing SHM, equation of motion is given as d2dt2+4x=0. Find the time period
View SolutionA particle starting from rest. Its acceleration (a) versus time (t) is as shown in the figure.
The maximum speed of the particle will be.
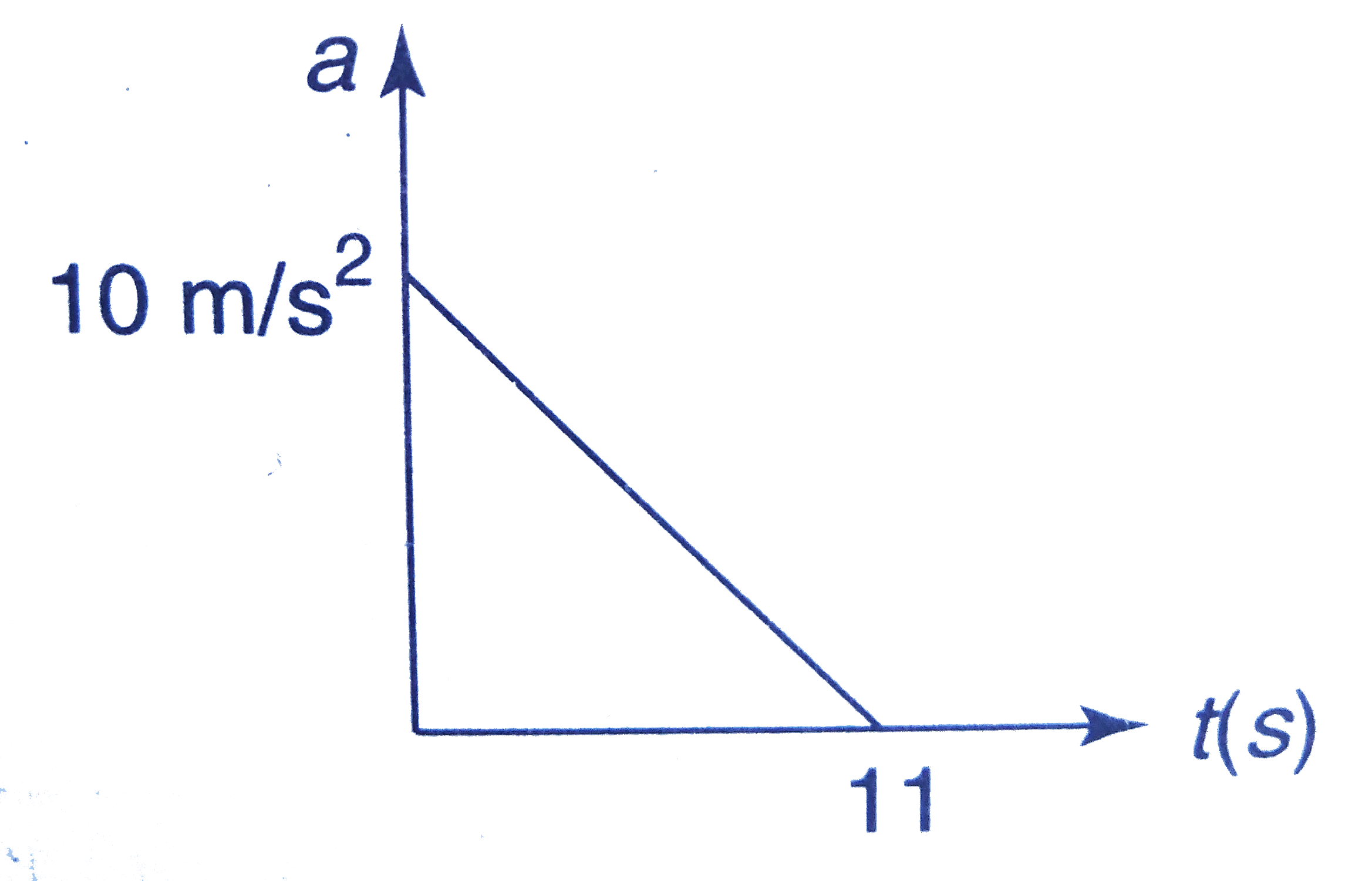
View SolutionA particle starting from rest. Its acceleration (a) versus time (t) is as shown in the figure.
The maximum speed of the particle will be.

View Solution