Passage XIII) Mr. Anoop having mass 50 kg is standing on a massless platform which oscillates up and down (doing SHM) of frequency 0.5 sec−1 and amplitude 0.4m. Platforms has a weighing machine fitted in it (Which is also massless). On which Anoop is standing. (Take (π2) = 10 and g = 10 m/s2. Assume that at t=0 (Platform+Anoop) is at their highest point of oscillation. [More than one option is correct]
![Passage XIII) Mr. Anoop having mass 50 kg is standing on a massless platform which oscillates up and down (doing SHM) of frequency 0.5 sec^(-1) and amplitude 0.4m. Platforms has a weighing machine fitted in it (Which is also massless). On which Anoop is standing. (Take (pi^(2)) = 10 and g = 10 m//s^(2). Assume that at t=0 (Platform+Anoop) is at their highest point of oscillation. [More than one option is correct] Which of the following will be correct for reading of weighting machine](https://d10lpgp6xz60nq.cloudfront.net/physics_images/MPP_PHY_C11_E01_146_Q01.png)
Which of the following will be correct for reading of weighting machine
When reading is 55 kg, then compression will be 1.1m
When reading is 50 kg, then compression will be 1.0m
When reading is 50kg, then compression will be 1.1m
When reading is 55kg, then composition will be 1.0m
The correct Answer is:A, B
Step by step video & image solution for Passage XIII) Mr. Anoop having mass 50 kg is standing on a massless platform which oscillates up and down (doing SHM) of frequency 0.5 sec^(-1) and amplitude 0.4m. Platforms has a weighing machine fitted in it (Which is also massless). On which Anoop is standing. (Take (pi^(2)) = 10 and g = 10 m//s^(2). Assume that at t=0 (Platform+Anoop) is at their highest point of oscillation. [More than one option is correct] Which of the following will be correct for reading of weighting machine by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension types18videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Matrix matching type questions13videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Advanced34videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct3videos
SEMICONDUCTORS AND ELECTRONIC DEVICES
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)38videos
SOLVD PAPERS 2017 NEET, AIIMS & JIPMER
Similar Questions
A person normally weighing 60kg stands on a platform which oscillates up and down harmonically at a frequency 2.0sec−1 and an amplitude 5.0cm . If a machine on the platform gives the person's weight against time deduce the maximum and minimum reading it will shown, Takeg=10m/sec2.
View SolutionA man of mass m=2kg is standing on a platform of mass M=5kg, then at any instant.
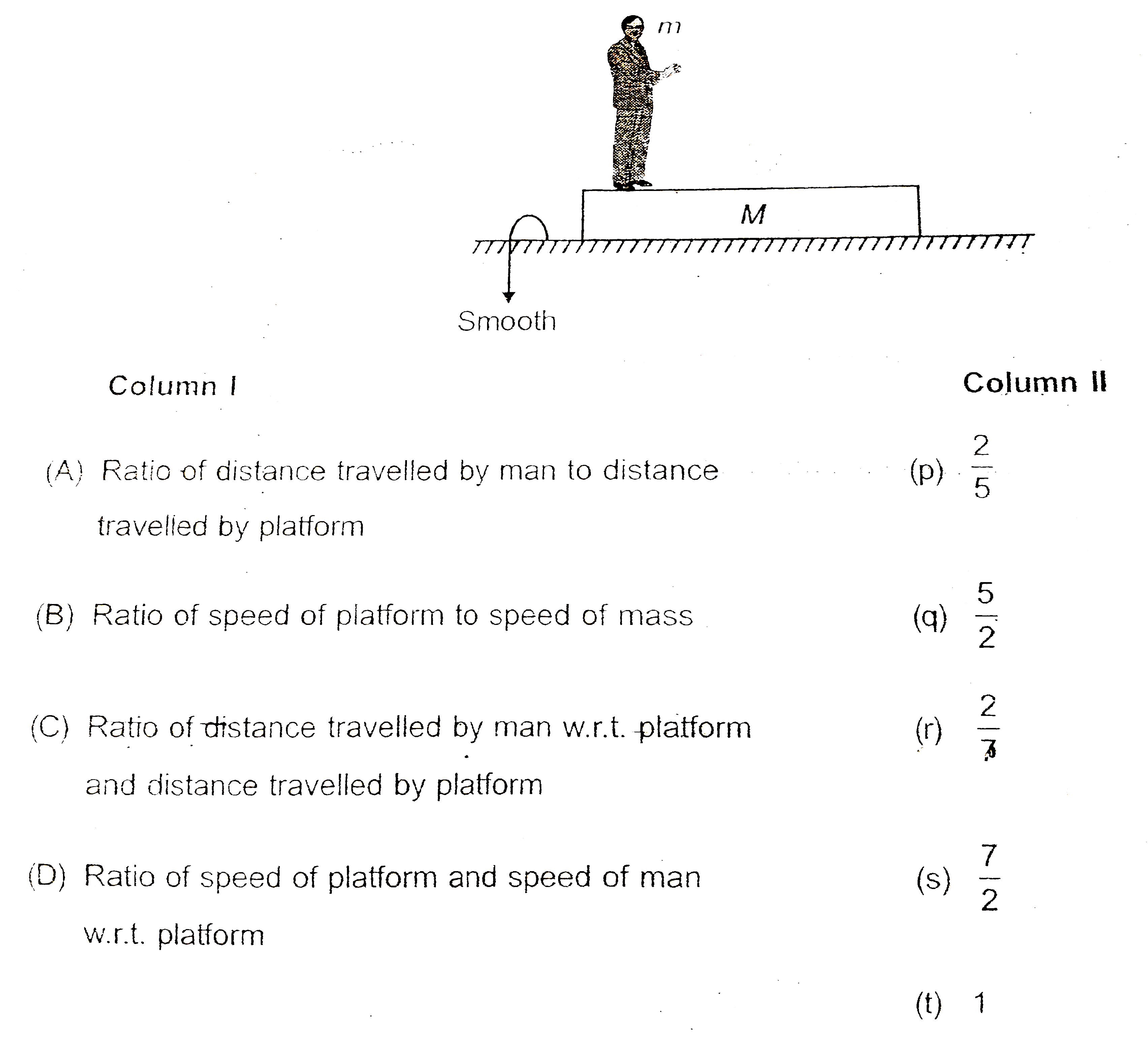
View Solution
Knowledge Check
- Question 1 - Select One
A simple harmonic oscillator has a frequency of 2.5 Hz and an amplitude of 0.05m. What is the period of the oscillations?
A0.4sB0.2sC8sD20s
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0s−1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons wieght against time.
(a) Will there be any change in weight of the body, during the oscillation?
(b) If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?View SolutionA man is standing on a platform moving up and down as a S.H.M. will there be any change in his weight as recorded by a weighing machine on the platform ?
View SolutionA man of mass 40kg is standing on a weighting machine kept on the floor of an elevator which is moving up with an acceleration of 2m/s2 Find the reading of the weighing maching.
View SolutionA man of mass 40kg is standing on a weighting machine kept on the floor of an elevator which is moving up with an acceleration of 2m/s2 Find the reading of the weighing maching.
View SolutionA man is standing on a sparing platform, Reading of spring balaance is 60kg wt If man jumps outside the platform then the reading of the spring balance .
View SolutionA man is standing on a sparing platform, Reading of spring balaance is 60kg wt If man jumps outside the platform then the reading of the spring balance .
View SolutionFind the natural frequency of oscillation of the system as shown in figure. Pulleys are massless and frictionless. Spring and string are also massless. (Take π2=10)
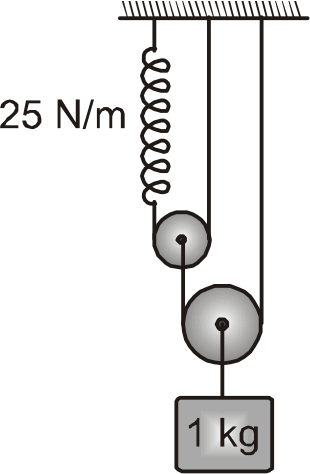
View Solution