Pendulum A is a physical pendulum made from a thin, rigid and uniform rod whose length is d. One end of this rod is attached to the ceiling by a frictionless hinge, so that the rod is free to swing back and forth. Pendulum B is a simple pendulum whose length is also d. Obtain the ratio TATB of their periods for small angle oscillations.
The correct Answer is:A
To find the ratio of the periods of Pendulum A (a physical pendulum) and Pendulum B (a simple pendulum), we will follow these steps:
Step 1: Determine the period of Pendulum A (Physical Pendulum)
The formula for the period TA of a physical pendulum is given by:
TA=2π√Imgh
Where:
- I is the moment of inertia about the pivot point,
- m is the mass of the pendulum,
- g is the acceleration due to gravity,
- h is the distance from the pivot to the center of mass.
For a uniform rod of length d, the moment of inertia I about one end is:
I=13md2
The center of mass of the rod is located at a distance d2 from the pivot. Thus, h=d2.
Substituting these values into the formula for TA:
TA=2π
⎷13md2mg⋅d2
Step 2: Simplify the expression for TA
Now we simplify the expression:
TA=2π
⎷13d2g⋅d2
This simplifies to:
TA=2π√2d3g
Step 3: Determine the period of Pendulum B (Simple Pendulum)
The formula for the period TB of a simple pendulum is given by:
TB=2π√Lg
For Pendulum B, the length L is equal to d:
TB=2π√dg
Step 4: Find the ratio TATB
Now, we can find the ratio of the periods:
TATB=2π√2d3g2π√dg
The 2π cancels out:
TATB=√2d3g√dg
Step 5: Simplify the ratio
This simplifies to:
TATB=√2√3=√23
Final Result
Thus, the ratio of the periods of Pendulum A to Pendulum B is:
TATB=√23≈0.816
The formula for the period TA of a physical pendulum is given by:
- I is the moment of inertia about the pivot point,
- m is the mass of the pendulum,
- g is the acceleration due to gravity,
- h is the distance from the pivot to the center of mass.
⎷13md2mg⋅d2
Now we simplify the expression:
⎷13d2g⋅d2
The formula for the period TB of a simple pendulum is given by:
Now, we can find the ratio of the periods:
This simplifies to:
Thus, the ratio of the periods of Pendulum A to Pendulum B is:
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
There is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
View SolutionA thin uniform rod of length l is pivoted at its upper end. It is free to swing in a vertical plane. Its time period for oscillation of small amplitude is
View SolutionThe free end of a simple pendulum is attached to the ceiling of a box. The box is taken to a height and the pendulum is oscillated. When the bob is at its lowest point the box is released to fall freely. As seen from the box during this period the bob will
View SolutionA uniform rod of length l oscillates about an axis passing through its end. Find the oscillation period and the reduced length of this pendulum.
View SolutionThe string of a simple pendulum replaced by a uniform rod of length L and mass M while the bob has a mass m. It is allowed to make small oscillation. Its time period is
View SolutionIn a free space, a thin rod carrying uniformly distributed negative charge −q is placed symmetrically along the axis of a tin ring of radius R varrying uniformly dostributed charge Q. The mass of the rod is m and length is l=2R. The ring is fixed and the rod is free to move. The rod is displaced slightly along the axis of the ring and then released. Find the period T to the small amplitude oscillations of the rod.
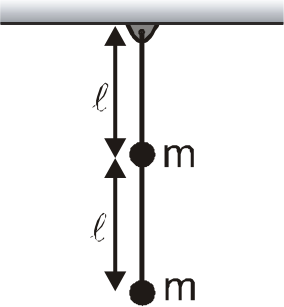
View SolutionTwo particle of mass m each are fixed to a massless rod of length 2l . The rod is hinged at one end about a smooth hinge and it performs oscillations of small angle in vertical plane. The length of the equivalent simple pendulum is:
View SolutionA simple pendulum of length 5 m is suspended from the ceiling of a cart. Cart is sliding down on a frictionless surface having angle of inclination 60°. The time period of the pendulum is
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionA thin rod of length L is hanging from one end and free to oscillate like s compound pendulum about a horizontal axis, Its time period for small oscillations is
View Solution
