The free end of a simple pendulum is attached to the ceiling of a box. The box is taken to a height and the pendulum is oscillated. When the bob is at its lowest point the box is released to fall freely. As seen from the box during this period the bob will
continue its oscillation as before
stop
will go in a circular path
move on a straight line
The correct Answer is:C
To solve the problem step by step, we will analyze the scenario of the pendulum bob inside the falling box.
Step 1: Understand the Setup
We have a simple pendulum attached to the ceiling of a box. The box is initially at rest and is taken to a height. The pendulum is oscillated, and when the bob is at its lowest point, the box is released to fall freely.
Hint: Visualize the scenario by drawing the box and the pendulum. Identify the forces acting on the bob when the box is in free fall.
Step 2: Identify Forces Acting on the Bob
When the box is released to fall freely, both the box and the pendulum bob experience the same gravitational acceleration (g). In the frame of reference of the box, the box is in free fall, and thus, it does not exert any normal force on the bob.
Hint: Remember that in free fall, all objects experience the same acceleration due to gravity.
Step 3: Analyze the Motion of the Bob
In the frame of the box, which is a non-inertial frame (because it is accelerating downwards), we need to consider the effects of pseudo forces. The bob will experience a pseudo force acting upwards equal to its weight (mg) because the box is falling downwards.
Hint: Think about how forces balance out in a non-inertial frame. The pseudo force acts in the opposite direction of the acceleration of the frame.
Step 4: Determine the Resultant Motion
At the lowest point of the pendulum's swing, the forces acting on the bob are:
- The gravitational force (downwards) = mg
- The pseudo force (upwards) = mg
Since these two forces cancel each other out, the only force acting on the bob is the inertia due to its horizontal velocity (if any).
Hint: Consider what happens to the motion of the bob when the forces cancel out.
Step 5: Conclusion on the Motion of the Bob
Since the bob is not acted upon by any net vertical force, it will not oscillate as it would normally do. Instead, it will continue moving horizontally due to its initial velocity, following a straight line path.
Hint: Reflect on the concept of inertia: an object in motion will remain in motion unless acted upon by a net external force.
Final Answer
As seen from the box during this period, the bob will move on a straight line.
We have a simple pendulum attached to the ceiling of a box. The box is initially at rest and is taken to a height. The pendulum is oscillated, and when the bob is at its lowest point, the box is released to fall freely.
When the box is released to fall freely, both the box and the pendulum bob experience the same gravitational acceleration (g). In the frame of reference of the box, the box is in free fall, and thus, it does not exert any normal force on the bob.
In the frame of the box, which is a non-inertial frame (because it is accelerating downwards), we need to consider the effects of pseudo forces. The bob will experience a pseudo force acting upwards equal to its weight (mg) because the box is falling downwards.
At the lowest point of the pendulum's swing, the forces acting on the bob are:
- The gravitational force (downwards) = mg
- The pseudo force (upwards) = mg
Since the bob is not acted upon by any net vertical force, it will not oscillate as it would normally do. Instead, it will continue moving horizontally due to its initial velocity, following a straight line path.
As seen from the box during this period, the bob will move on a straight line.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
15 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - worked out Examples
22 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
If the string of an oscillating simple pendulum is cut, when the bob is at the mean position, the bob falls along a parabolic path.
The bob possesses horizontal velocity at the mean position.
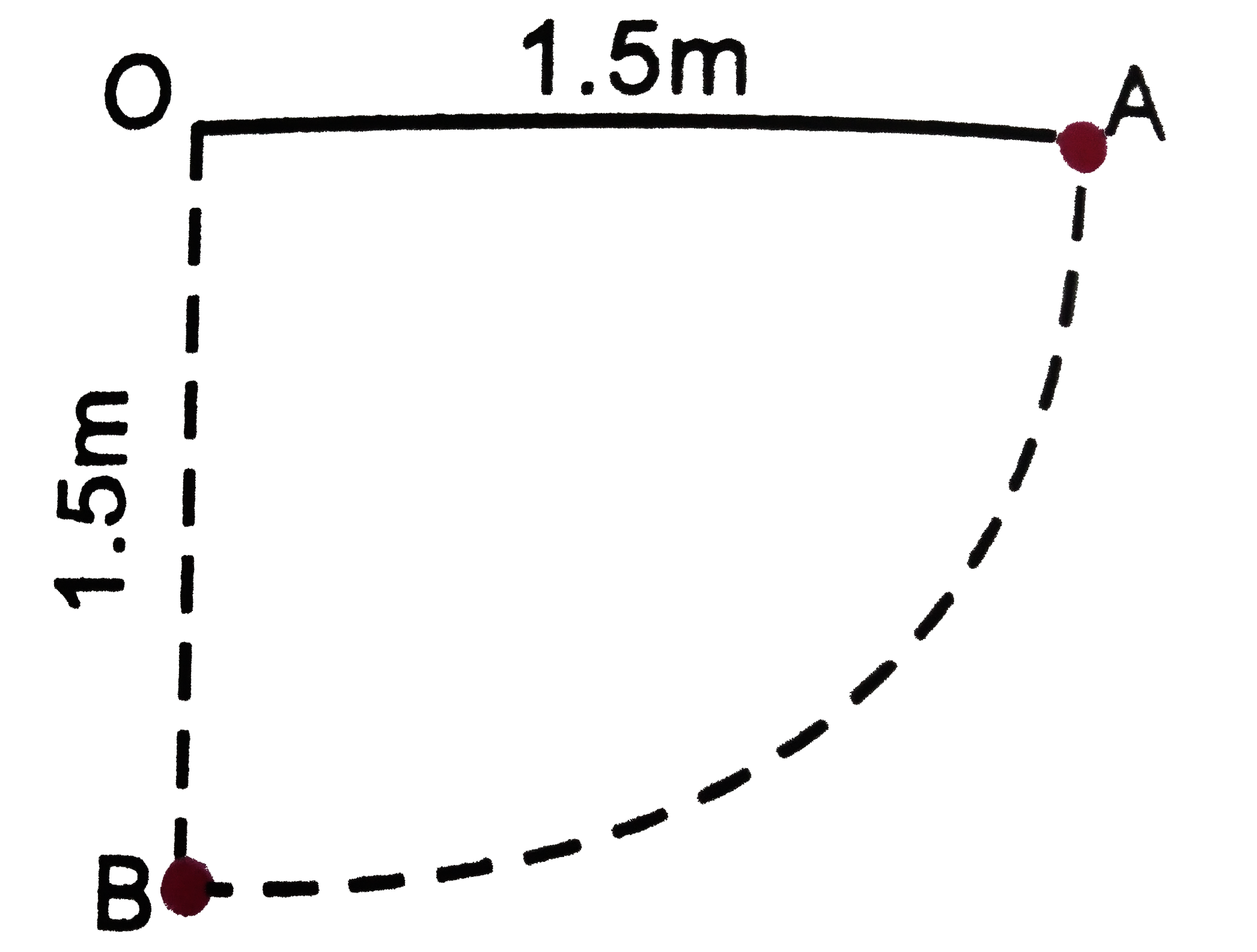
View SolutionThe bob A of a simple pendulum is released from a horizontal position A as shownin in figure. If the length of the pendulum is 1.5m , what is the speed with which the bob arrives at the lowermost point B, given that it dissipates 5% of its initial energy against air resistance ?
View SolutionWhat is the period of oscillation of a simple pendulum if its bob is made of ice ?
View SolutionThe bob of a simple pendulum is displaced from its equilibrium position 'O' to a position 'Q' which is at a height 'h' above 'O' and the bob is then released. Assuming the mass of the bob to be 'm' and time period of oscillation to be 2.0s, the tension in the string when the bob passes through 'O' is
View SolutionThe bob of a simple pendulum is displaced from its equilibrium position 'O' to a position 'Q' which is at a height 'h' above 'O' and the bob is then released. Assuming the mass of the bob to be 'm' and time period of oscillation to be 2.0s, the tension in the string when the bob passes through 'O' is
View SolutionA box is placed on a smototh plane end it is free to move. A single penldulum is attached in the block. Find its time period.

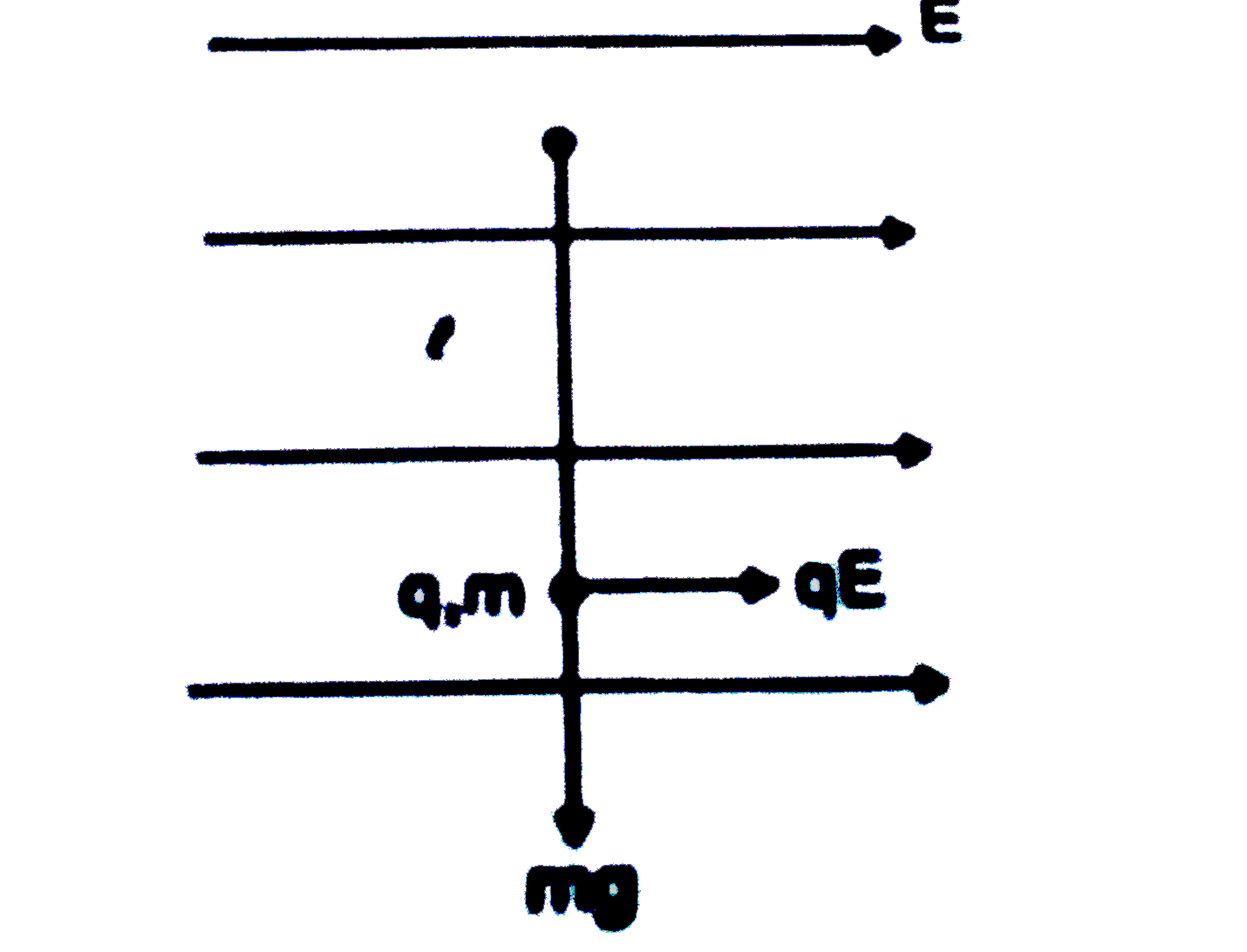
View SolutionA simple pendulum has a length l & mass of bob m. The bob is given a charge q coulomb. The pendulum is suspended in a uniform horizontal electric field of strength E as shown in figure, then calculate the time period of oscillation when bob is slightly displaced from its mean position.
View SolutionIn a simple pendulum, the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle θ with the vertical.
View SolutionA simple pendulum is oscillating without damiping, When the displacement of the bob is less than maximum, its acceleration vector →a is correctly show in:
View SolutionThe bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the stirng at this instant.
View Solution