Prove that an ideal capacitor in ac circuit does not dissipate power.
To prove that an ideal capacitor in an AC circuit does not dissipate power, we will follow these steps:
Step 1: Understand the AC Voltage and Current Relationships
Consider a capacitor with capacitance C connected to an alternating source of emf given by:
E(t)=E0sin(ωt)
where E0 is the peak voltage and ω is the angular frequency.
Step 2: Determine the Current Through the Capacitor
In a capacitive circuit, the current I(t) leads the voltage E(t) by a phase angle of π2 radians. Therefore, the current can be expressed as:
I(t)=I0sin(ωt+π2)
Using the trigonometric identity, we can rewrite this as:
I(t)=I0cos(ωt)
where I0 is the peak current.
Step 3: Calculate RMS Values
The root mean square (RMS) values for voltage and current are given by:
Erms=E0√2,Irms=I0√2
Step 4: Determine the Phase Difference
The phase difference ϕ between the voltage and current in a capacitive circuit is:
ϕ=π2
Step 5: Calculate Average Power
The average power Pavg in an AC circuit is given by:
Pavg=Erms⋅Irms⋅cos(ϕ)
Substituting the values we have:
Pavg=(E0√2)⋅(I0√2)⋅cos(π2)
Step 6: Evaluate the Cosine Term
Since cos(π2)=0, we find:
Pavg=(E0√2)⋅(I0√2)⋅0=0
Conclusion
Thus, the average power dissipated by an ideal capacitor in an AC circuit is:
Pavg=0
This proves that an ideal capacitor does not dissipate power in an AC circuit.
---
Consider a capacitor with capacitance C connected to an alternating source of emf given by:
E(t)=E0sin(ωt)
where E0 is the peak voltage and ω is the angular frequency.
In a capacitive circuit, the current I(t) leads the voltage E(t) by a phase angle of π2 radians. Therefore, the current can be expressed as:
I(t)=I0sin(ωt+π2)
Using the trigonometric identity, we can rewrite this as:
I(t)=I0cos(ωt)
where I0 is the peak current.
The root mean square (RMS) values for voltage and current are given by:
Erms=E0√2,Irms=I0√2
The phase difference ϕ between the voltage and current in a capacitive circuit is:
ϕ=π2
The average power Pavg in an AC circuit is given by:
Pavg=Erms⋅Irms⋅cos(ϕ)
Substituting the values we have:
Pavg=(E0√2)⋅(I0√2)⋅cos(π2)
Since cos(π2)=0, we find:
Pavg=(E0√2)⋅(I0√2)⋅0=0
Thus, the average power dissipated by an ideal capacitor in an AC circuit is:
Pavg=0
This proves that an ideal capacitor does not dissipate power in an AC circuit.
Similar Questions
Knowledge Check
Phase difference between voltage and current in a capacitor in an ac circuit is
AπBπ/2C0Dπ/3Assertion : The only element that dissipates energy in an ac circuit is the resistive element.
Reason : There are no power losses associated with pure capacitances and pure inductances in an ac circuit.AIf both assertion ans reason are true ans reaason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion istrue but reason is false.DIf both assertion and reason are false.
In an LCR circuit the energy is dissipated in
View Solution(i) When an ac source is connected to an ideal capacitor show that the average power supplied by the source over a complete cycle is zero.
(ii) A lamp is connected in series with a capacitor. Predict your observation when the system is connected first across a dc and an ac source. What happence in each case if the capacitance of the capacitor is reduced ?
View Solution2.5πμF capacitor and 3000−ohm resistance are joined in series to an AC source of 200volts and 50sec−1 frequency. The power factor of the circuit and the power dissipated in it will respectively
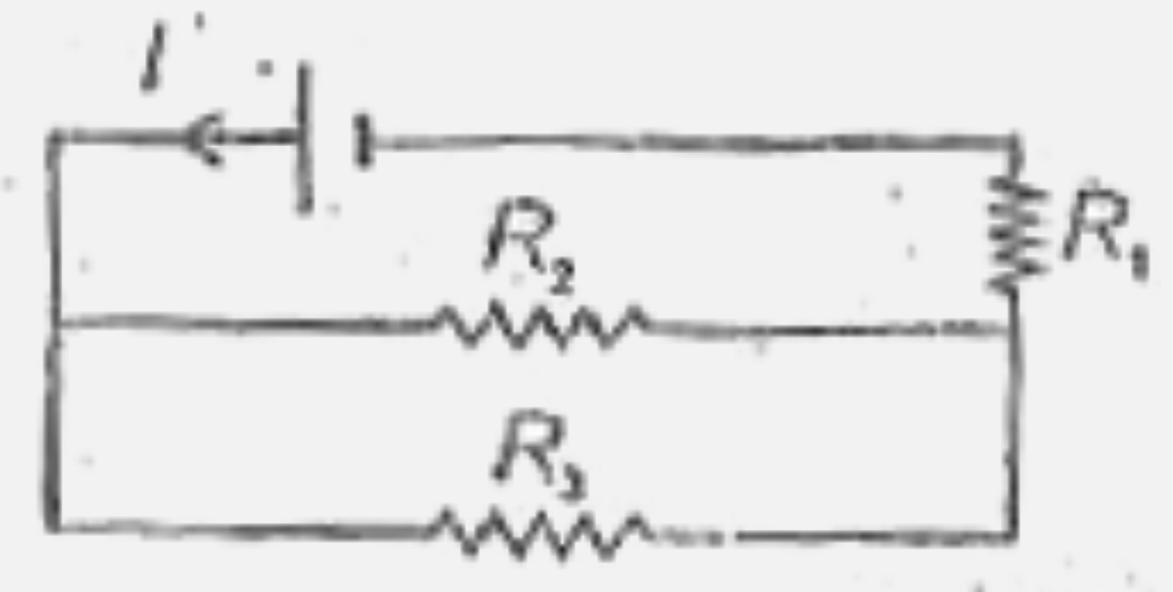
View SolutionRefer to the circuit shown . What will be the total power dissipation in the circuit if P is the power dissipated in R1 ? It is given that R2=4R1 and R3=12R1
View SolutionIf V0 and I0 are the peak current and voltge across the resistor in a series L−C−R circuit, then the power dissipated in the circuit is (powerfac→r=cosθ)
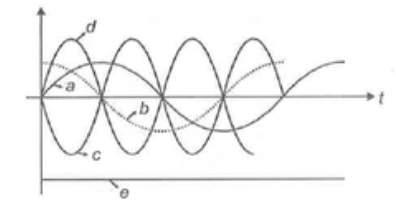
View SolutionIf an ac source is connected across ideal capacitor and current passing through it is denoted by curve (a) then instantaneous power is denoted by curve
View Solution