In an LCR circuit the energy is dissipated in
L only
C only
R only
all of these
The correct Answer is:C
To solve the question about energy dissipation in an LCR circuit, we can follow these steps:
Step 1: Understand the Components of the LCR Circuit
An LCR circuit consists of three main components:
- Inductor (L): Stores energy in the form of a magnetic field.
- Capacitor (C): Stores energy in the form of an electric field.
- Resistor (R): Dissipates energy as heat.
Step 2: Identify the Nature of the Supply
The circuit is connected to an AC (Alternating Current) supply. This is important because the behavior of the components differs from that in a DC (Direct Current) circuit.
Step 3: Analyze Energy Dissipation
In an AC circuit:
- The resistor (R) dissipates energy in the form of heat due to the current flowing through it. This is known as power dissipation.
- The inductor (L) and capacitor (C) do not dissipate energy; instead, they store and release energy. The energy in the inductor and capacitor oscillates back and forth but does not result in energy loss.
Step 4: Conclusion
Since only the resistor dissipates energy in the LCR circuit, we conclude that the energy is dissipated in the resistor (R).
Final Answer
The energy is dissipated in the resistor (R) in an LCR circuit.
---
An LCR circuit consists of three main components:
- Inductor (L): Stores energy in the form of a magnetic field.
- Capacitor (C): Stores energy in the form of an electric field.
- Resistor (R): Dissipates energy as heat.
The circuit is connected to an AC (Alternating Current) supply. This is important because the behavior of the components differs from that in a DC (Direct Current) circuit.
In an AC circuit:
- The resistor (R) dissipates energy in the form of heat due to the current flowing through it. This is known as power dissipation.
- The inductor (L) and capacitor (C) do not dissipate energy; instead, they store and release energy. The energy in the inductor and capacitor oscillates back and forth but does not result in energy loss.
Since only the resistor dissipates energy in the LCR circuit, we conclude that the energy is dissipated in the resistor (R).
The energy is dissipated in the resistor (R) in an LCR circuit.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -2 Part-1
14 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -2 Part-2
6 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - HIGH LEVEL PROBLEMS
11 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
Similar Questions
If V0 and I0 are the peak current and voltge across the resistor in a series L−C−R circuit, then the power dissipated in the circuit is (powerfac→r=cosθ)
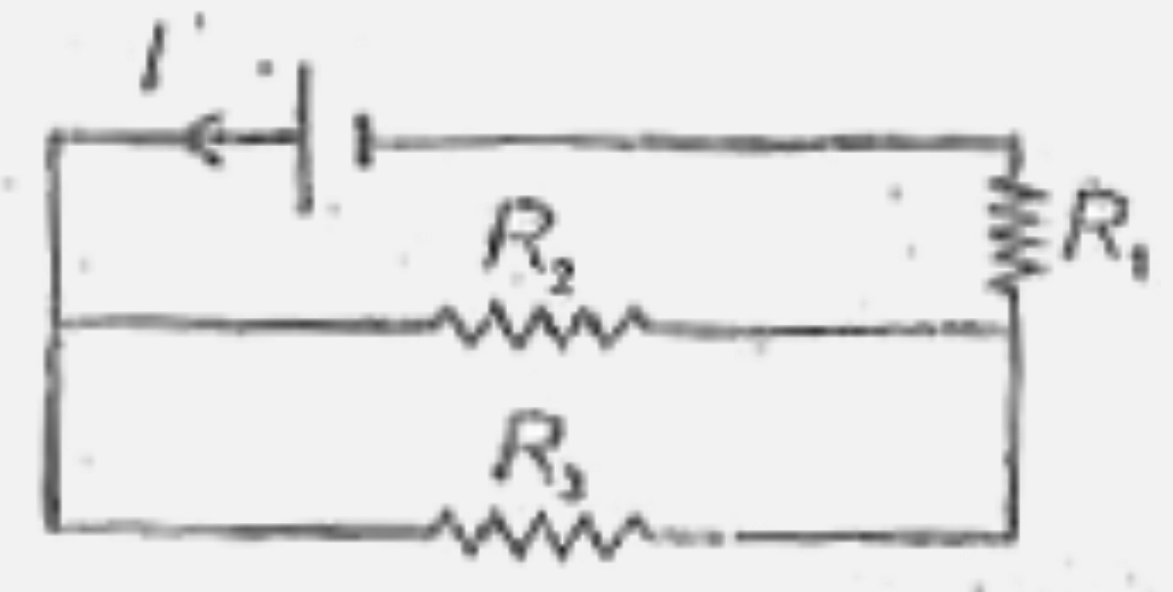
View SolutionRefer to the circuit shown . What will be the total power dissipation in the circuit if P is the power dissipated in R1 ? It is given that R2=4R1 and R3=12R1
View SolutionIn the circuit shown, the average power dissipated in the resistor is (assume diode to be ideal)
View SolutionIn an LCR circuit, the capacitance is made one-fourth, when in resonance. Then what should be the change in inductance, so that the circuit remains in resonance?
View SolutionIn an LCR circuit, the capacitance is made one-fourth, when in resonance. Then what should be the change in inductance, so that the circuit remains in resonance?
View SolutionA voltage V=V0sinωt is applied to a series LCR circuit. Derive expression for the average power dissipated over a cycle.
Under What condition (i) no power is dissipated even though the current flows through the circuit?
(ii) Maximum power is dissipated in the circuit?
View SolutionIn series LCR circuit at resonance
View SolutionIn a LCR oscillatory circuit find the energy stored in inductor at resonance. If voltage of source is 10 V and resistance is 10Omega and inductance = 1H.
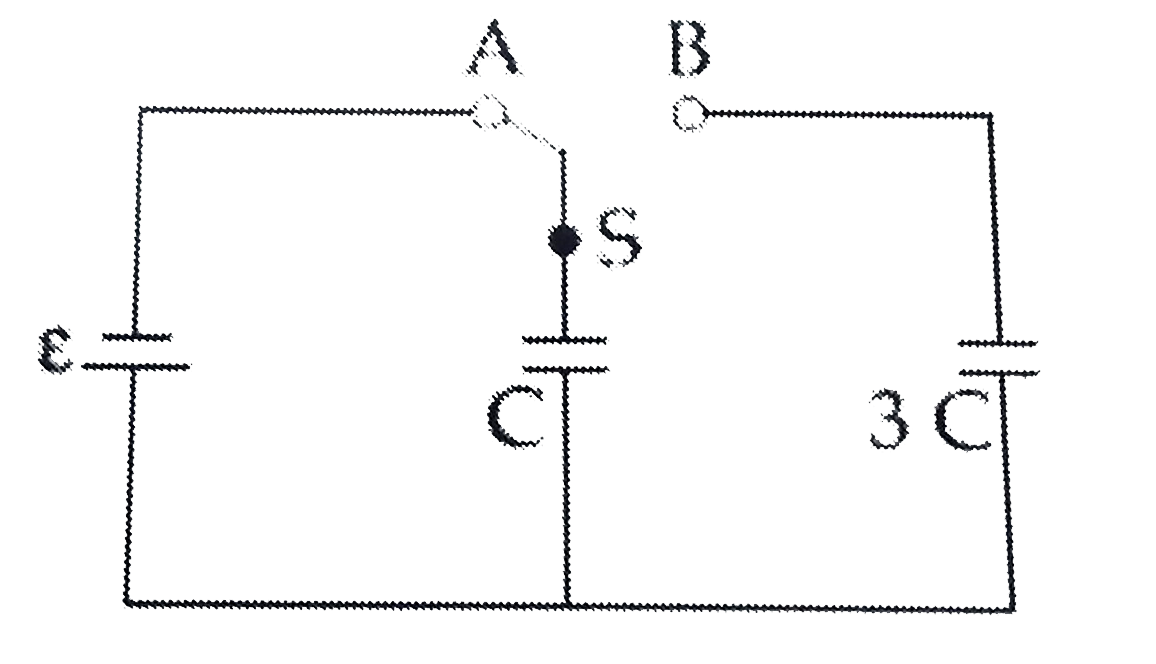
View SolutionIn the figure shown , after the switch 's' is turned from postion 'A' to postion 'B' the energy dissipated in the circuit in terms of capactance 'C' and total charge 'Q' is :
View SolutionA series AC circuit contains an inductor (20mH), a capacitor (100μF), a resistor (50Ω) and an AC source of 12V,50Hz. Find the energy dissipated in the circuit in 1000s.
View Solution
