Red light of wavelength $5400 Å$ from a distant source modulated wave of $60 %$ modulattion by using a condenser of capacity 250 pF in parallel with a load resistnce $100 k Ω$ . Find the maximum modulated frequency which could be detected by it.

1.89 mm

4mm

1 mm

3mm

Text Solution

Verified by Experts

The correct Answer is:A

Here, wavelength $λ = 5400 Å = 5.4 \times 10^{- 7}$ m,
a=0.80 mm = $8 \times 10^{- 4}$ m, D=1.4m
$∴$ Distance between first two dark bands on each side of central maximum is the width of central maximum
$= 2 x = \frac{2 λ D}{d} = \frac{2 \times 5.4 \times 10^{- 7} \times 1.4}{8 \times 10^{- 4}}$
$= 1.89 \times 10^{- 3}$ m =p1.89 m

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A diode detector is used to detect an amplitudennodulated wave of $60 %$ modulation by using a condence of capacity $250$ picodarad in parallel with a load resistance $100$ kilo obm find the maximum modulated which could be find the maximum modalated frequency which could be detected by it
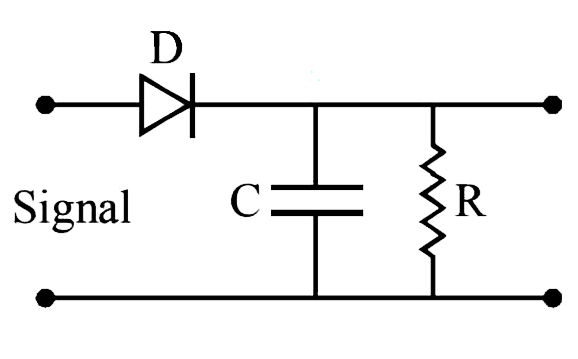A $10.62 M H z$
B $10.62 k H z$
C $5.31 M H z$
D $5.31 k H z$
Question 2 - Select One
Consider the parallel resonant circuit shown in adjacent figure. One branch contains an inductor of inductance L and a small ohmic resistance R, whereas the other branch contains a capacitor of capacitance C. The circuit is fed by a source of alternating emf $E = E_{o} e^{j ω t} = E_{o} sin ω t$
The impedance of inductor branch, $Z (1) = R + j ω L$
The impendence of capacitor branch, Z(2) = (1//jomegaC) $t h e r e f o u r N e t i m p e d a n c e Z o f t h e t w o p a r a l \leq l b r a n c h e s i s g i v e n b y $ (1)/(Z)=(1)/(Z_(1))+ (1)/)Z_(2)=(1)/(R+jomegaC $$ =(R-jomegaL)/(jomegaL)(R-jomegaL)+jomegaC=(R)/(R^(2)+omega^(2)+L^(2))+jomega[C-(L)/(R^(2)+omegaL^(2))] $ T h e c u r r e n t f l o w \in g \in t h e \circ u i t $ I=(E)/(Z)=(E)[(R)/(R^(2)+omega^(2)L^(2))+jomega(C-(L)/(R^(2)+omega^(2)L^(2)))] $ F or r e s o n a n c e \to o u r, t h e c u r r e n t μ s t b e \in p h a s e w i t h t h e a p p l i e d e m f . F or t h i s, t h e r e a c t i v e c o m p o \neq n t o f c u r r e n t s h o d - - b e z e r o, l . e . $ omega[C-(L)/(R^(2)+omega^(2)L^(2))]=0 $ or$ C=(L)/(R^(2)+omega_(r)^(2)L^(2)) $(w r i t \in g$ omega_(r) $f or$ omega $a t r e s o n a n c e) T h i s g i v e s r e s o n a n t a n g a - - r e q u e n c y $ omega_(r)=sqrt((1)/(LC)-R^(2)/(L^(2))) At parallel circuit resonance, theimpendence is maximum and current is minimum. Parallel resonant circuit is sometimes called the anti-resonance in order to distinguish from series resonance
QFind the impedance of AC circuit at resonance shown in the adjacent figure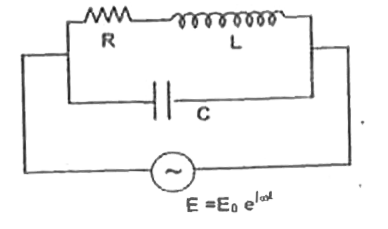

A coil of inductance 100 muH and 60 Omega effective resistance is connected in parallel with a condenser of 100 pF. The resonant circuit so formed is excited from an alternating current source. The frequency of the source is varied until the maximum impendence of the circuit is obtained. The frequency of the generator at which this occurs is approximately
A $(\frac{10^{2}}{2 π} H z$
B $(\frac{10^{7}}{2 π} H z$
C $(\frac{10^{5}}{2 π} H Z$
D $(\frac{10^{3}}{2 π} H z$
Question 3 - Select One
The efficient transmission of signals is achieved by superimposing electrical audio signals on a high frequency carrier wave (the process is known as modulation). When the amplitude of high frequency carrier wave is changed in accordance with the intensity of modulating signal, it is called amplitude modulation. The extent to which the amplitude of carrier wave is changed by the signal is described by modulation factor. It is given as
$m = \frac{Amplitude change of carrier wave}{Amplitude of unmodulated carrier wave}$
Let a carrier wave is represented by
$V_{c} = V_{c} {cos ω}_{c} t$
Let the modulation factor be m, the maximum change in amplitude of carrier wave is $m V_{c}$
So, modulating signal can be represented as $v_{m} = m V_{c} {cos ω}_{m} t$
So, the amplitude of modulated wave is $= V_{c} + m V_{c} {cos ω}_{m} t$
Using this value, the instantaneous voltage of modulated wave is
$E = V_{c} {cos ω}_{c} t + \frac{m V_{c}}{2} cos (ω_{c} + ω_{m}) t + \frac{m V_{c}}{2} cos (ω_{c} - ω_{m}) t$
The above wave contains three frequencies namely, $f_{c}, f_{c} + f_{m}$ and $f_{c} - f_{m}$ . The frequencies $f_{c} + f_{m}$ and $f_{c} - f_{m}$ are called side band frequencies , USB and LSB respectively.
If modulation factor is 100% , the amplitude change of carrier wave is
AEqual to amplitude of modulating signal
BEqual to amplitude of unmodulated carrier wave
CEqual to amplitude of modulated wave
DEqual to zero

DC PANDEY-SOLVED PAPERS 2018-AIIMS

Home
Ask Doubt
Profile

Red light of wavelength 5400Å from a distant source modulated wave of 60% modulattion by using a condenser of capacity 250 pF in parallel with a load resistnce 100kΩ. Find the maximum modulated frequency which could be detected by it.

The correct Answer is:A

Here, wavelength λ=5400Å=5.4×10−7m, a=0.80 mm = 8×10−4m, D=1.4m ∴ Distance between first two dark bands on each side of central maximum is the width of central maximum =2x=2λDd=2×5.4×10−7×1.48×10−4 =1.89×10−3 m =p1.89 m

Topper's Solved these Questions

Similar Questions

Knowledge Check

A diode detector is used to detect an amplitudennodulated wave of 60% modulation by using a condence of capacity 250 picodarad in parallel with a load resistance 100 kilo obm find the maximum modulated which could be find the maximum modalated frequency which could be detected by it

DC PANDEY-SOLVED PAPERS 2018-AIIMS

Red light of wavelength $5400 Å$ from a distant source modulated wave of $60 %$ modulattion by using a condenser of capacity 250 pF in parallel with a load resistnce $100 k Ω$ . Find the maximum modulated frequency which could be detected by it.

A diode detector is used to detect an amplitudennodulated wave of $60 %$ modulation by using a condence of capacity $250$ picodarad in parallel with a load resistance $100$ kilo obm find the maximum modulated which could be find the maximum modalated frequency which could be detected by it