A plane light wave with wavelength λ=0.65μm falls normally on a large glass plate whose opposite side has a longrectangular recess 0.60mm wide. Using Fig. find the depth H of the recess at which the diffraction pattern on the screen 77cm away from the plate has the maximum illuminance at its centre.
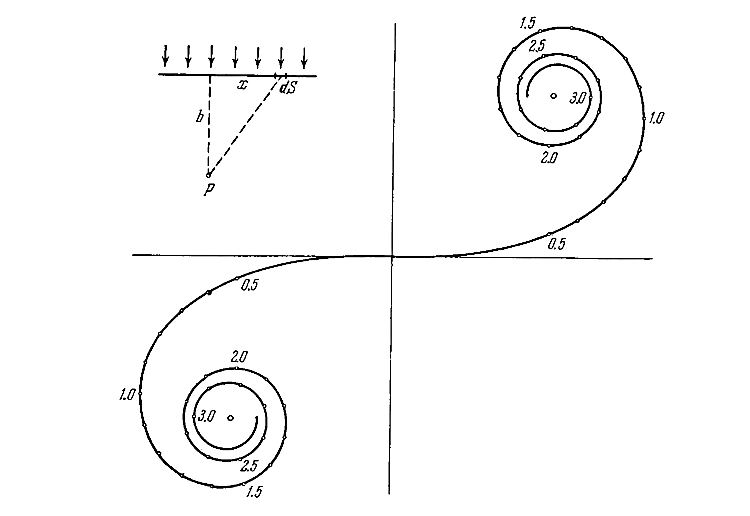
Let a=width of the reccess and
v=a2√2bλ=a√2bλ=0.6√2×0.77×0.65≅0.60
be the paremeter along Cornu's spiral corresponding to the half-width of the resecc. The amplitude of the diffracted wave is given by
_(~)const⎡⎢⎣eiδv∫−ve−iπu2/2du+∞∫ve−iπu2/2du+v∫−∞e−iπu22du⎤⎥⎦
where δ=2πλ(n−1)h
is the extra phase due to the recess. (Actually an extra phase e−iδ appears outside the recess. When we take it out and obsord it in the constant we get the expression written).
Thus the amplitude is

~const[(C(v)−iS(v))eiδ+(12−C(v))−i(12−S(v))]
From the cornu's spiral, the corrdinates corresponding to the parameter v=0.60 are
C(v)=0.57,S(v)=0.13
so the intensity at o is proportional to
∣∣[(0.57−0.13i)eiδ−0.07−i0.37]∣∣2
=(0.572+0.13)2+0.072+0.372
+(0.57−0.13i)(−0.07+0.37i)eiδ
+(0.57+0.13i)(−0.07−i0.37i)e−iδ
We write
0.57¯¯¯¯¯+0.13i=0.585e¯¯¯¯+iαα=12.8∘
−0.07±0.37i=0.377e±iββ=100.7∘
Thus the cross term is
2×0.585×0.377cos(δ+88∘)
=2×0.585×0.377cos(δ+π2)
For maximum intensity
δ+π2=2k'π,k'=1,2,3,4,.............
=2(k+1)π,k=0,1,2,3,.........
or δ=2kπ+3π2
so h=λn−1(k+34)
Topper's Solved these Questions
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Polarization Of Light
Explore 43 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Dispersion And Absorption Of Light
Explore 24 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Interference Of Light
Explore 33 Videos
- MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:MECHANICSExercise:Mechanics Problems
Explore 92 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
Similar Questions
A plane light wave with wavelength λ=0.65μm falls normally on a large glass plate whose opposite side has a large and an opaque strip of width a=0.30mm (Fig.) A screen is placed at a distance b=110cm from the plate. The height h of the ledge is such that the intensity of light at point 2 of the screen is the heighest possible. making use of Fig. find the ratio of intensities at point 1 and 2.
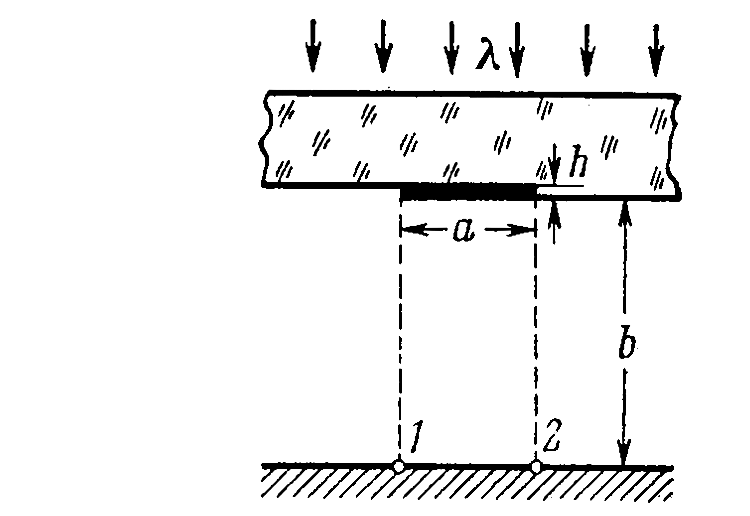
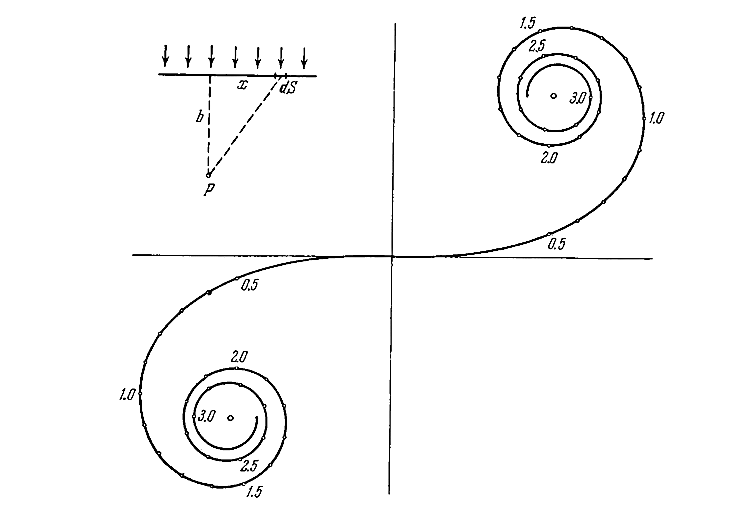
View SolutionA plane light wave wityh wavelength 0.60μm falls normally on a long opaque strip 0.70mm wide. Behind it a screen is placed at a distance 100cm. Using Fig. find the ratio of intensities of light in the middle of the diffraction pattern and at the edge of the geometrical shadow.
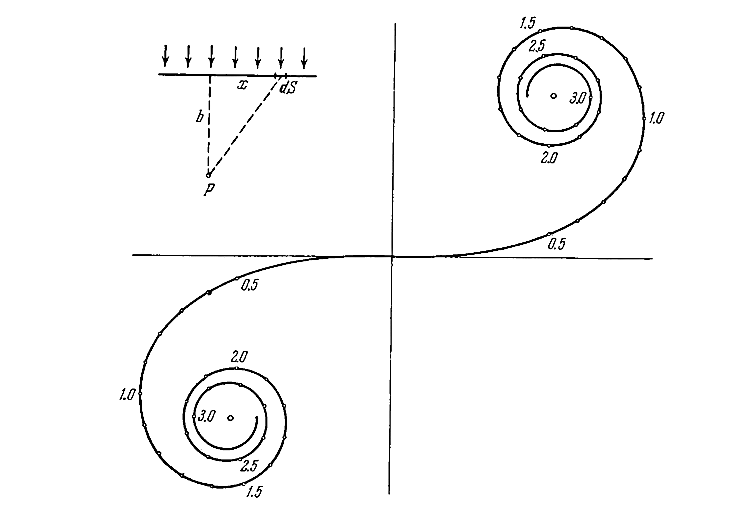
View Solution
Knowledge Check
Light of wavelength λ=5000Å falls normally on a narrow slit. A screen is placed at a distance of 1m from the slit and perpendicular to the direction of light. The first minima of the diffraction pattern is situated at 5mm from the centre of central maximum. The width of the slit is
A(a) 0.1mmB(b) 1.0mmC(c) 0.5mmD(d) 0.2mm
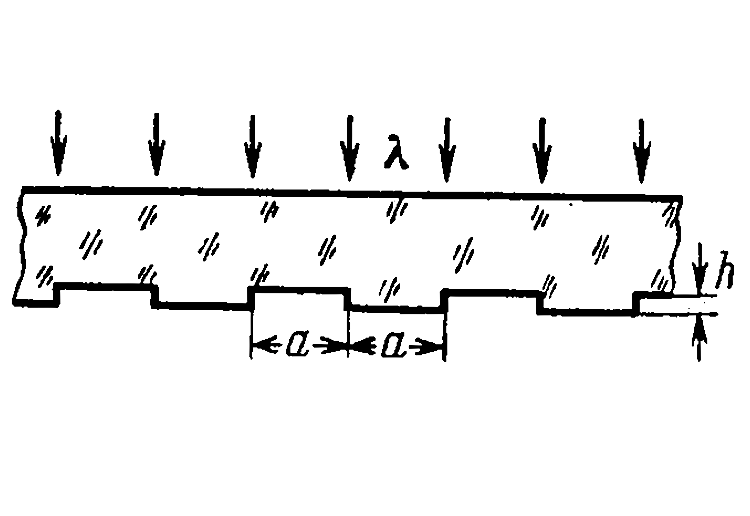
A plane light wave with wavelength λ falls normally on a phase diffraction grating whose side view is shown in Fig. The grating is cut on a glass plate with refractive index n. Find the depth h of the lines at which the intensity of the central Fraunhofer maximum is equal to zero. what is in this case the diffraction angle corresponding to the first maximum?
View SolutionA plane light wave with wavelength λ=0.60μm falls normally on a sufficiently large glass plate having a round recess on the oppiste side (Fig.) For the observation point P that recess correcponds to the first one and and a half Fresnel zones. Find the depth h of the recess at which the intensity of light at the point P is
(a) maximum,
(b) minimum,
(c ) equal to the intensity of incident light.
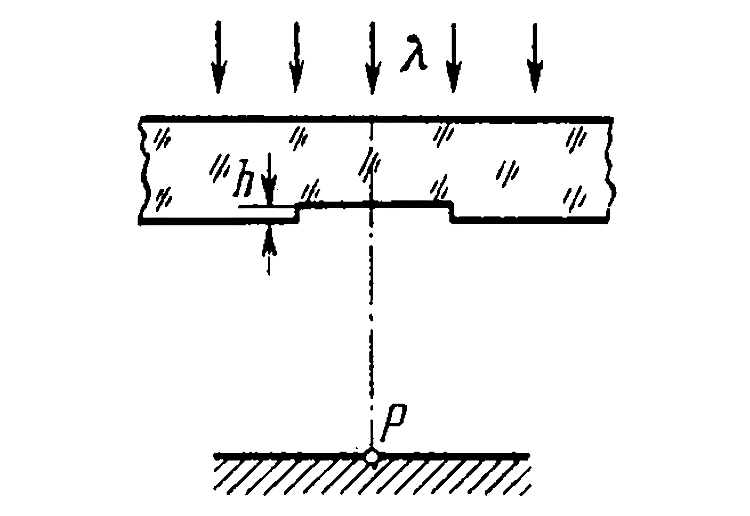
View SolutionA plane light wave with wavelength λ and intensity I0 falls normally on a large glass plate whose opposite side serves as an opaque screen with a round aperture equal to the first Fresnel zone for the observation point P. In the middle of the aperture there is a round recess equal to half the Fresnel zone. What must the depth h of that recess be for the intensity of light at the point P to be the highest? What is this intensity equal to?
View SolutionA plane light wave with wavelength λ=0.60μm and intensity I0 falls normally on a large glass plate whose side view is shown in Fig. At what height h of the ledge will be intensity of light at points located directly below be
(a) minimum,
(b) twice as low as I0 (the losses due to reflection are to be neglected).
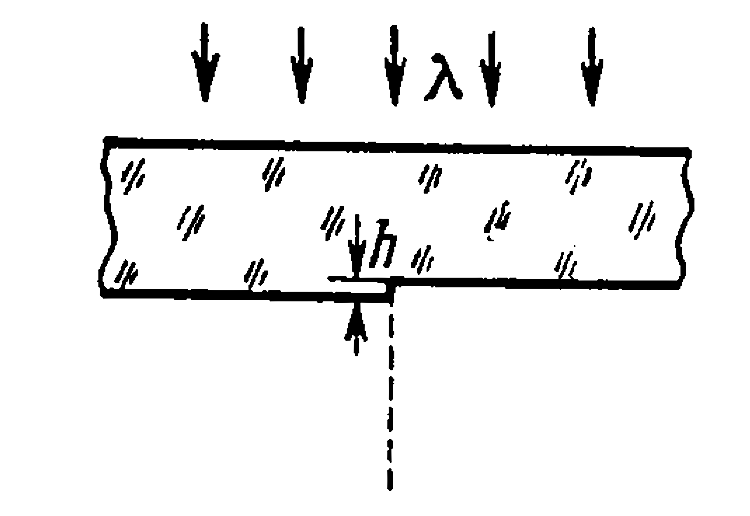
View SolutionLight of wavelength λ=5000Å falls normally on a narrow slit. A screen is placed at a distance of 1m from the slit and perpendicular to the direction of light. The first minima of the diffraction pattern is situated at 5mm from the centre of central maximum. The width of the slit is
View SolutionA parallel electron beam accelerated in an electric field with a potential difference of 15 V falls on a narrow rectangular diaphragm 0.08 mm wide. Find the width of the principal diffraction maximum on a screen placed 60 cm away from the diaphrugm.
View SolutionA parallel electron beam accelerated in an electric field with a potential difference of 15 V falls on a narrow rectangular diaphragm 0.08 mm wide. Find the width of the principal diffraction maximum on a screen placed 60 cm away from the diaphrugm.
View Solution
