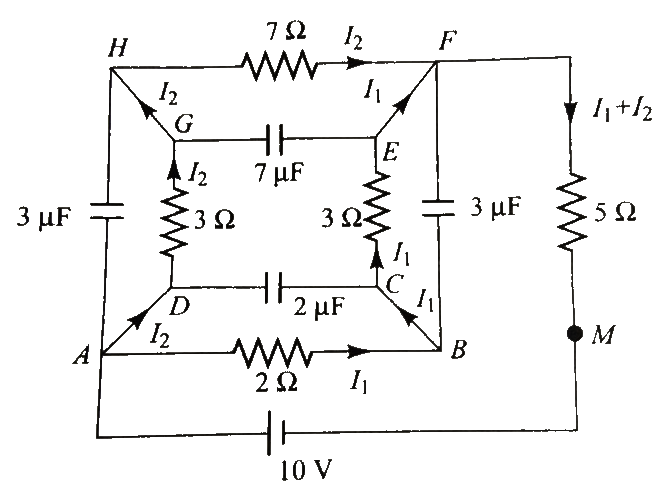
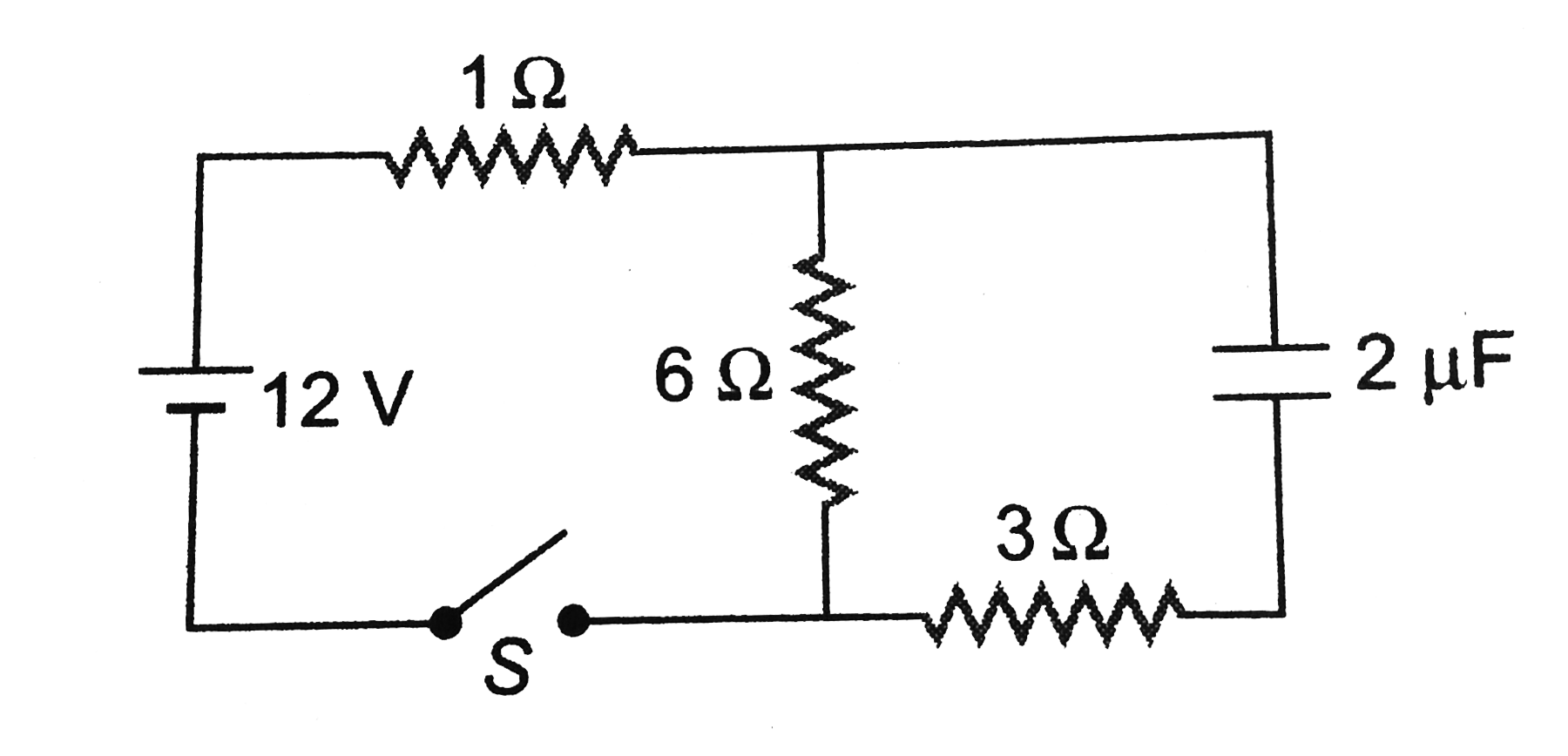
Refer to Fig. .
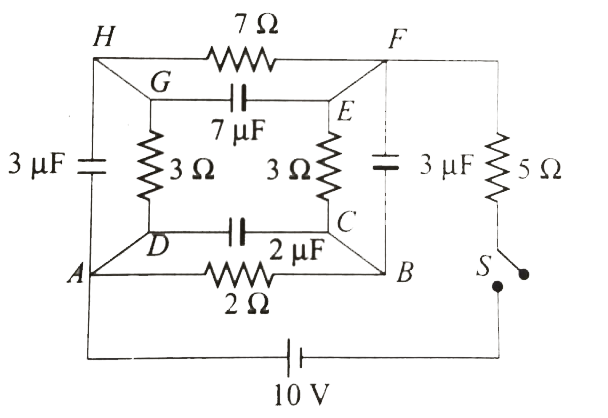
Long time after closing the switch , find the current through the resistor.
A
B
C
D
Video Solution
Text Solution
The correct Answer is:C
Initially, When all the capacitors are uncharged, they will act as conducting wires. Hence, all the resistances will be short - circuited. So no resistance occurs between . Thus current through the resistor will be .
In steady state, distibution of current is shown.
Loop
or .....(I)
Loop
or .......(ii)
From Eqs. (i) and (ii) ,
Hence , current through the is . Potential
difference across the capacitor is
Energy in it is given by
Potential difference across is capacitor is
Energy in it is given by
Potential difference across the capacitor is
Energy in it is given by
potential difference across the capacitor is
Energy in it is given by
Thus , whole of the energy stored in all capacitors will be dissipated after the switch is opened. So the energy dissipated is .
|
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Integer
5 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Calculating Thermal Power in Resistance
14 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Assertion - Reasoning
6 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type
4 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
Similar Questions
The current through the 5Ω resistor is
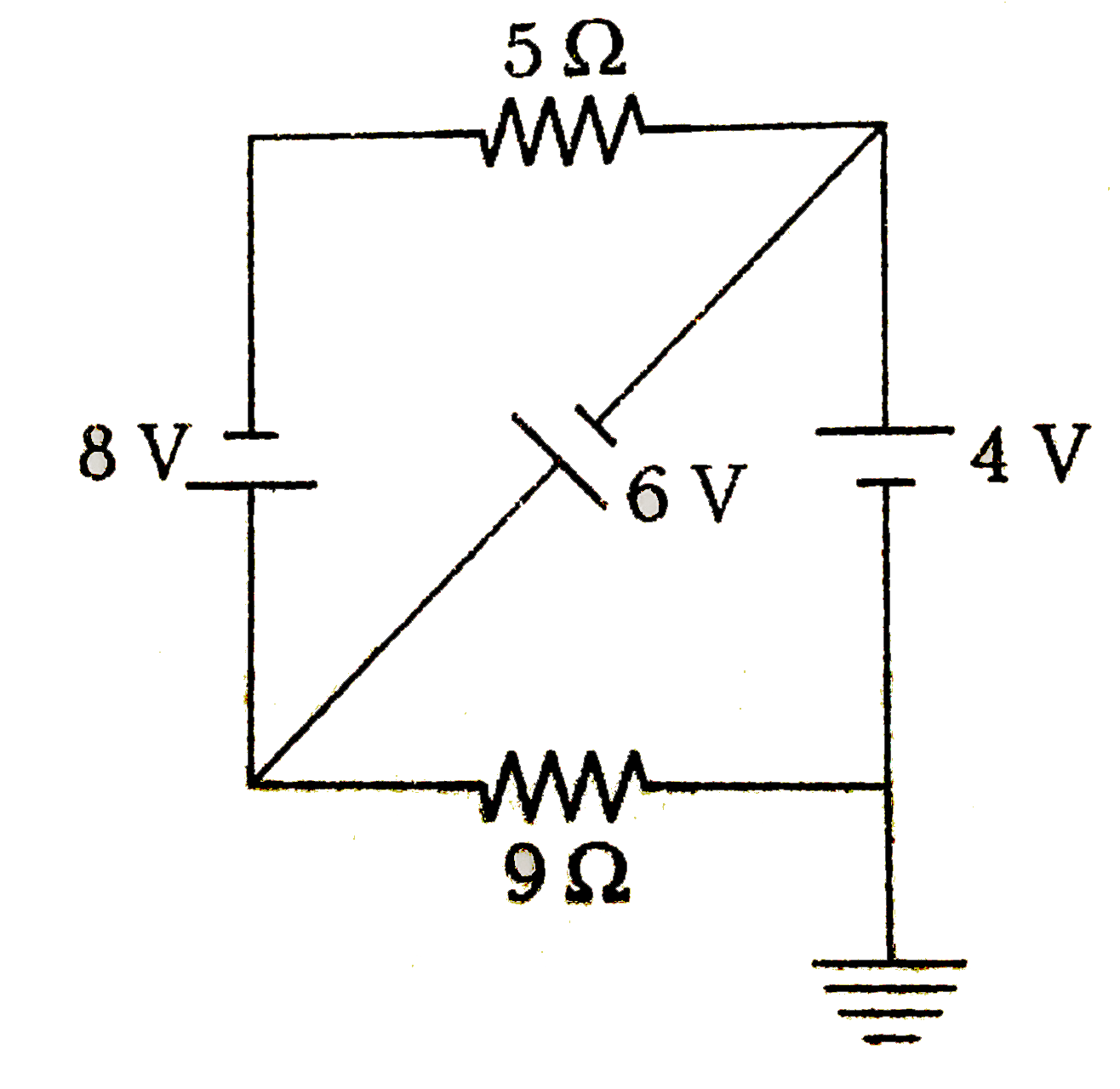
View SolutionCurrent through the 5Ω resistor is
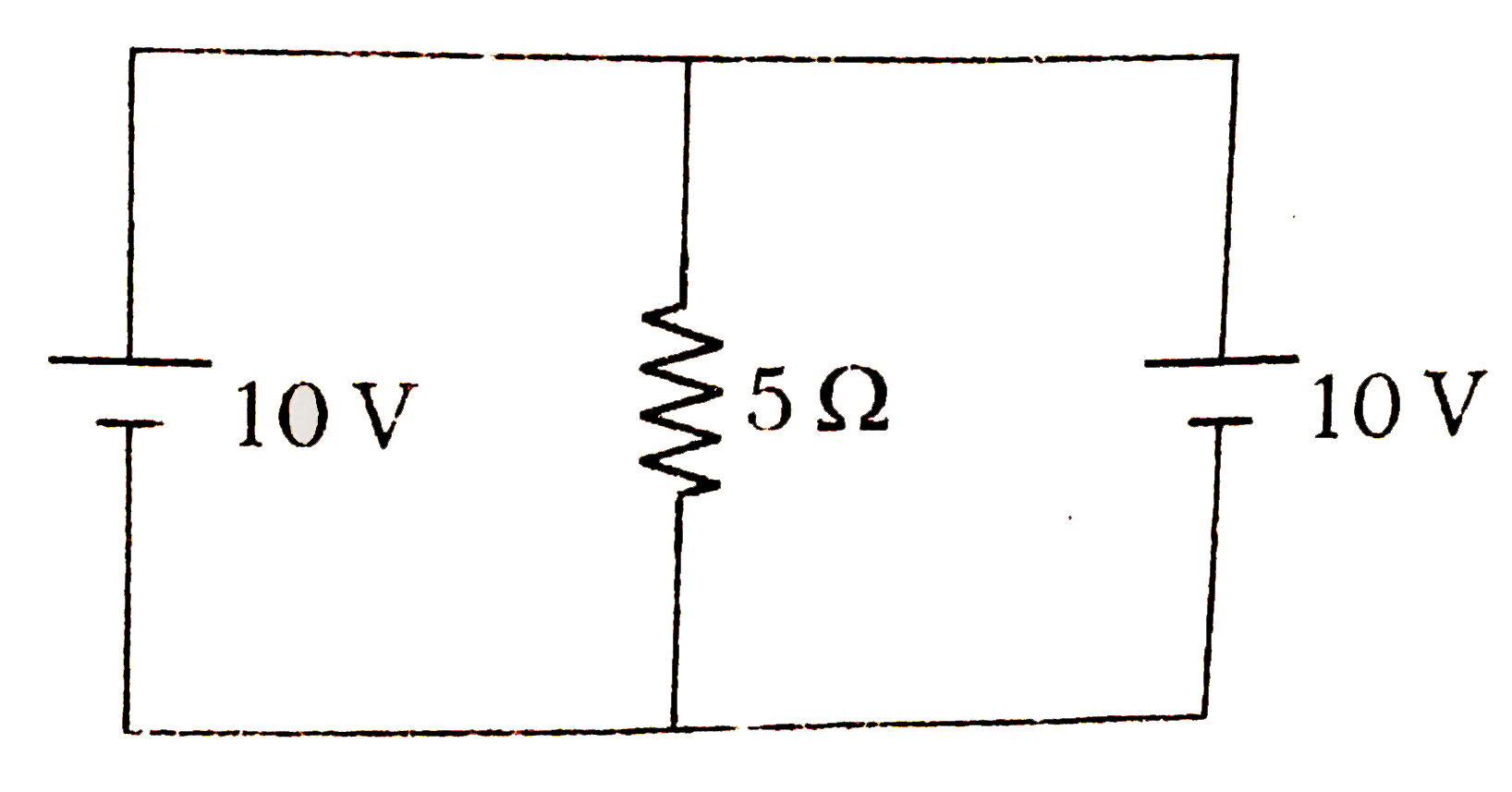
View SolutionFind the current through 12Ω resistor in
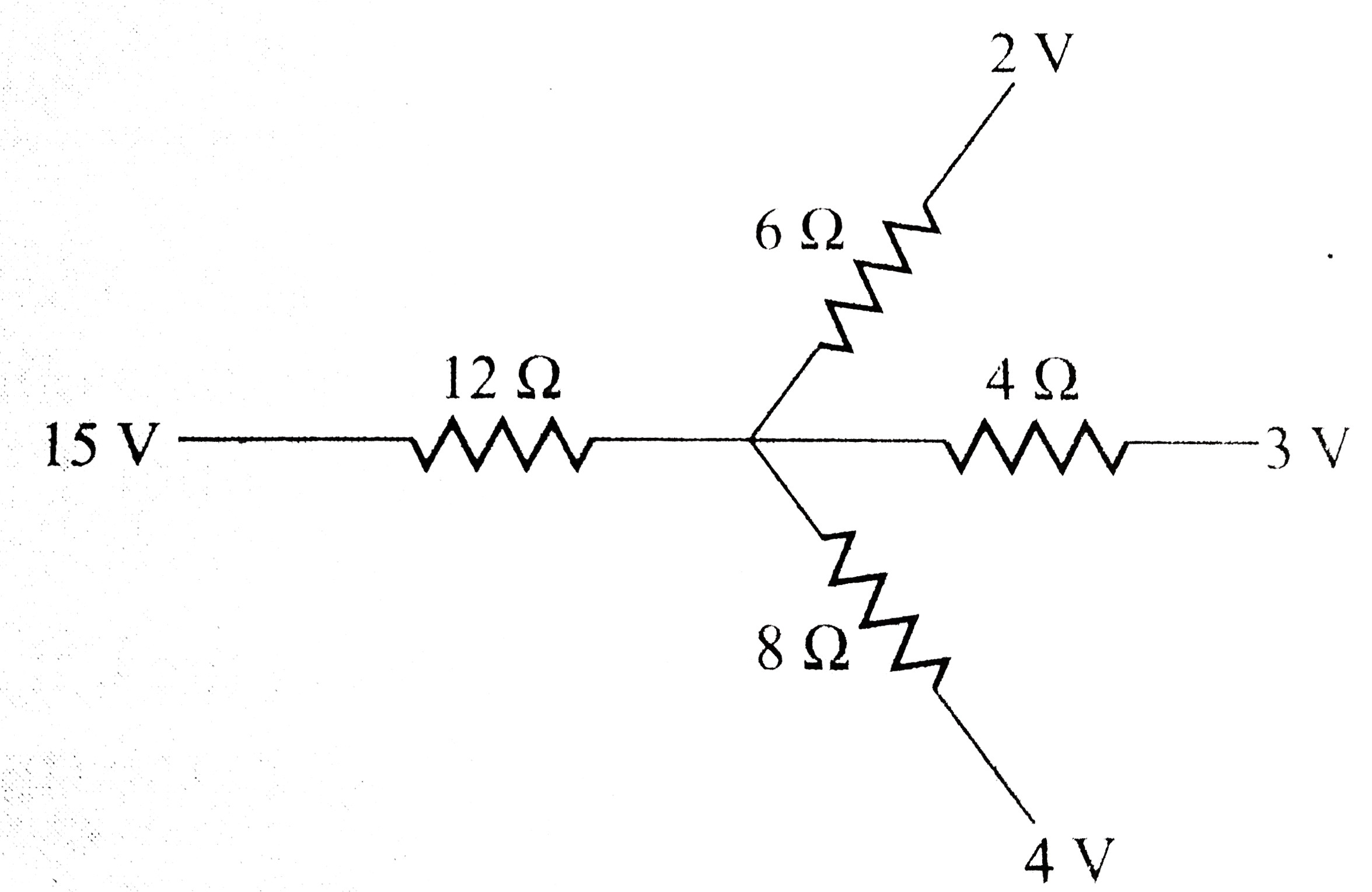
View SolutionRefer to Fig. 7.49.
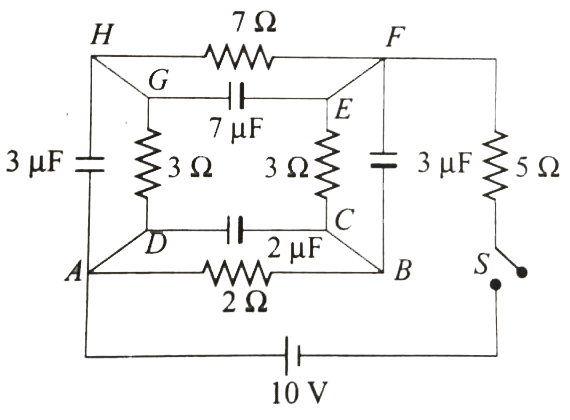
At t=0 , the switch is closed . Just after closing the switch, find the current through the 5Ω resistor.
View SolutionFind the current through the 10(Ω)resistor shown in figure.
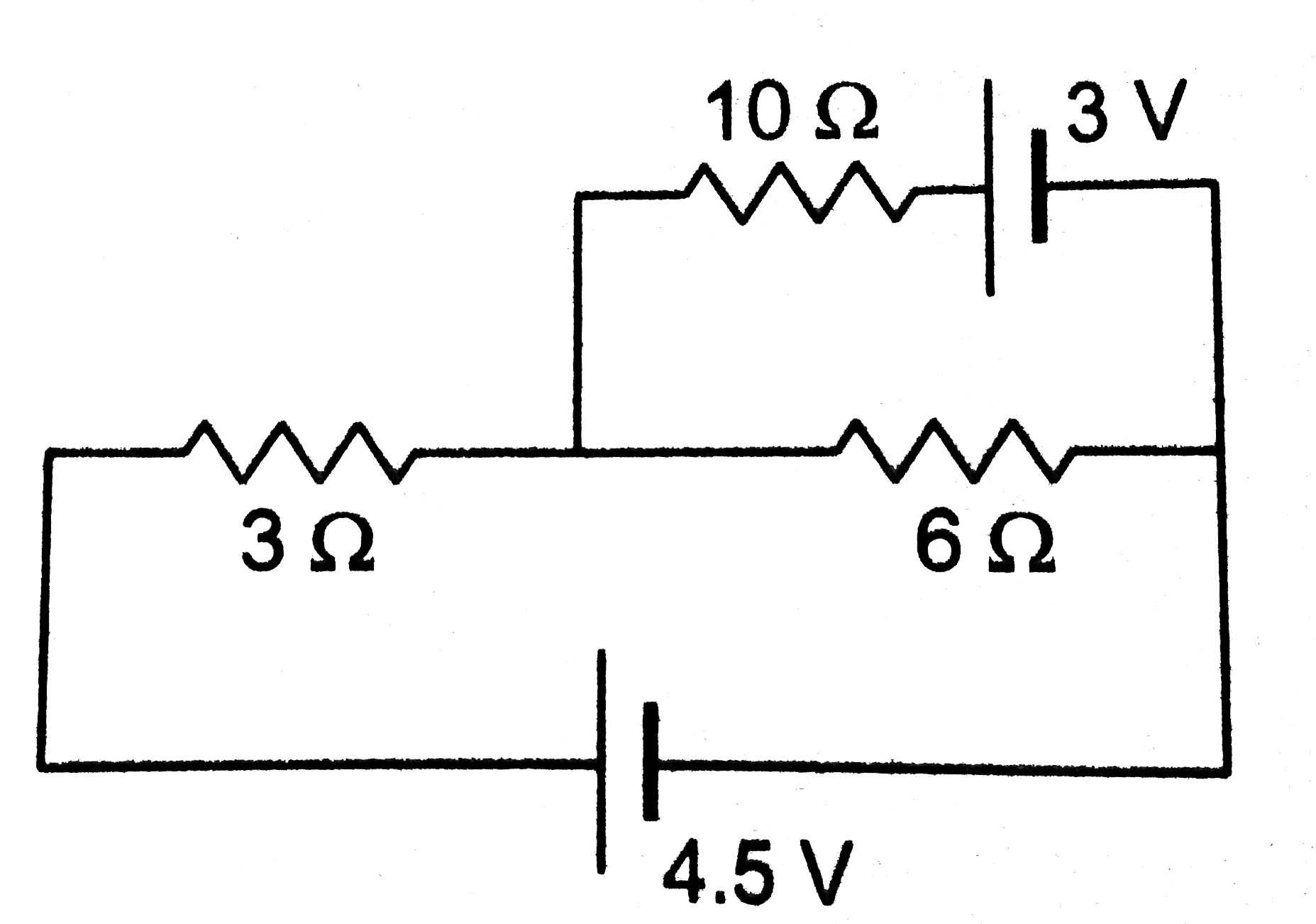
View SolutionFind the current through the 10(Ω)resistor shown in figure.

View SolutionThe value of current through 2Ω resistor is
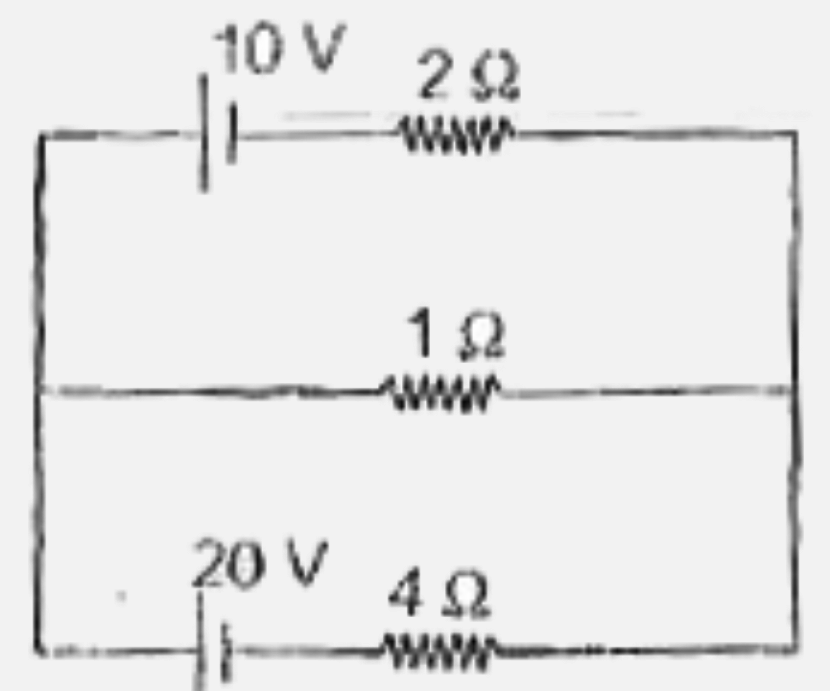
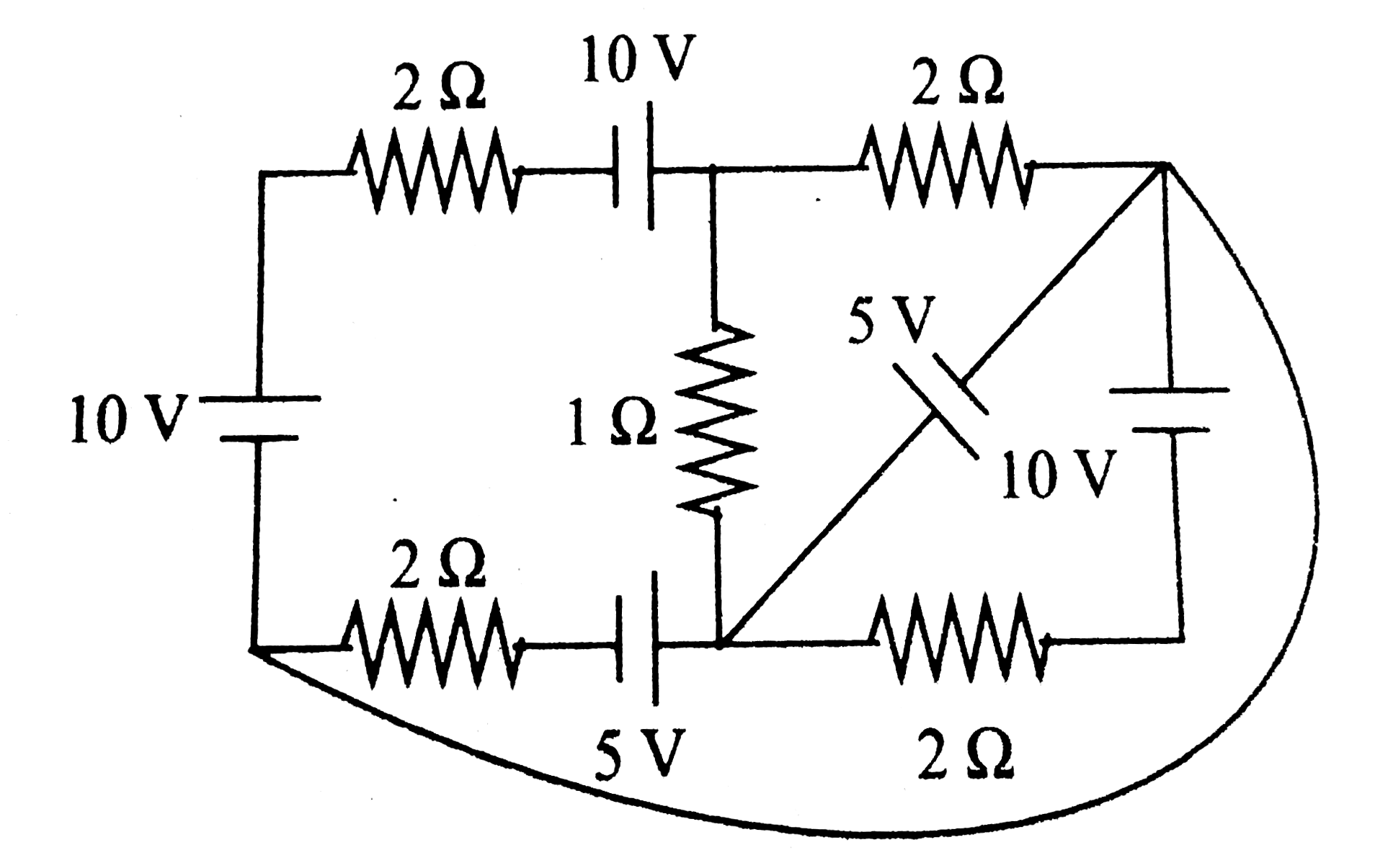
View SolutionWhen the switch is closed, the initial current through the 1Ω resistor is
View SolutionIn the circuit diagram shown in find the current through the 1Ω resistor.
View SolutionElectric current through 400Ω resistor is :
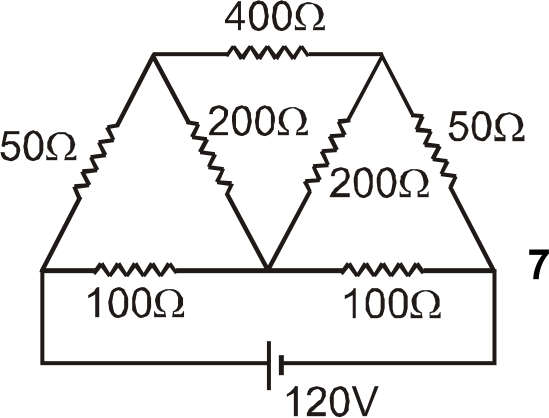
View Solution
