Referring to a−x graph, find the velocity when thedisplacement of the particle is 100m. Assume intial velocity as zero.
 .
.
We can find relation between a and x as:
Using (y−y1=(y2−y1x2−x(1)(x−x1
(a−3)=6−3250−50(x−50)⇒a=3100x+32
 .
.
But v=√v20+2(A)
As v0=0⇒v2=2∫adx
⇒a=3100x32
⇒v2=2 [Area of (a-x) graph upto x=100m]
=2[12(32+92)100]=600⇒v=10√6ns−1.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A particle moves along the x-axis obeying the equation x=t(t−1)(t−2), where x is in meter and t is in second
a. Find the initial velocity of the particle.
b. Find the initial acceleration of the particle.
c. Find the time when the displacement of the particle is zero.
d. Find the displacement when the velocity of the particle is zero.
e. Find the acceleration of the particle when its velocity is zero.
View SolutionReferring to a−s diagram as shown in , findthe velocity of the particle when the particle when the spaarticle justcovers 20m, (v0=√50ms−1.
 .
.
View SolutionRefering to v−s diagram, find:
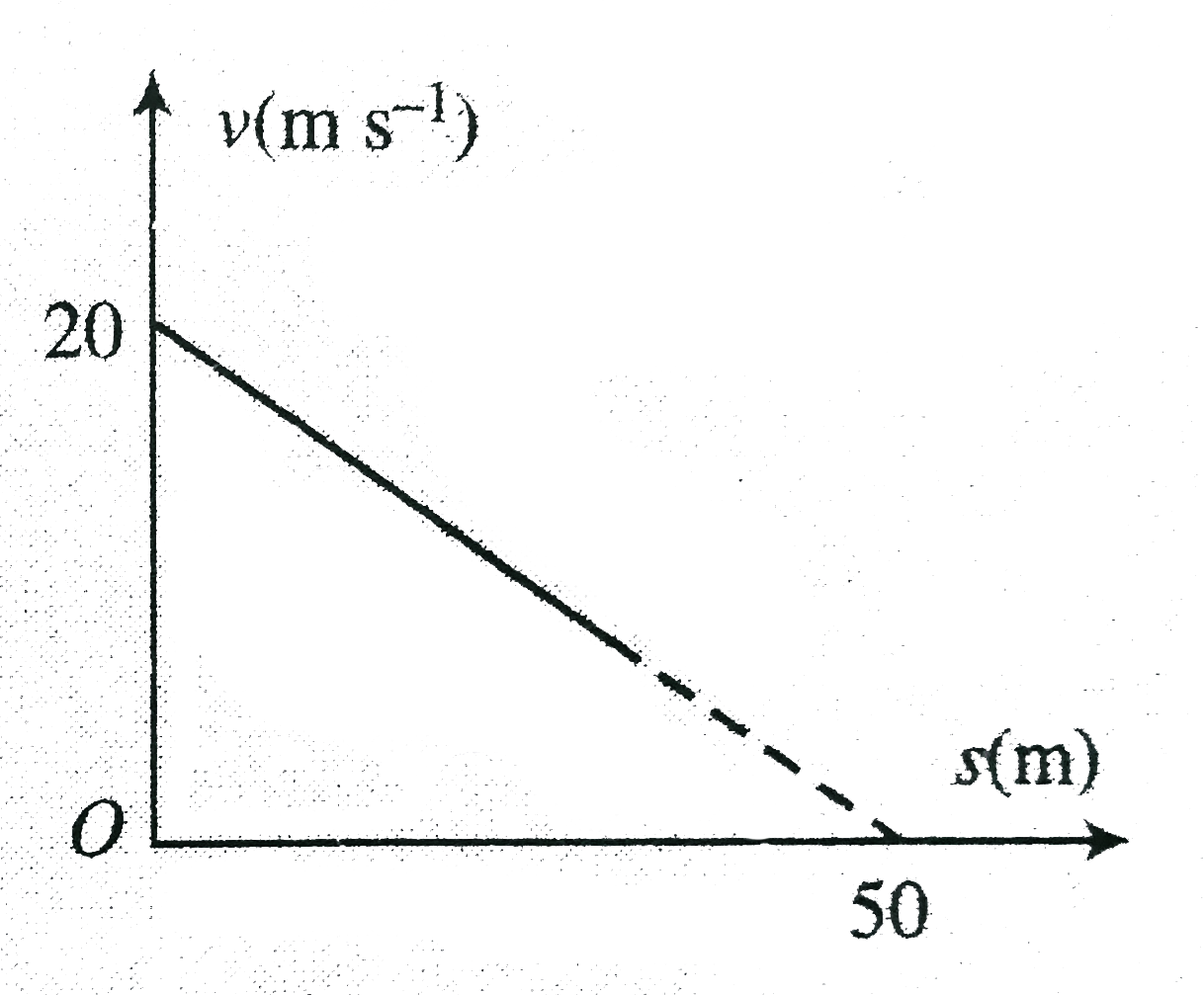 .
.
a. Acceleration of the particle when its velocity becomes half of the initial velocity.
b. Total distance covered by the particle.
View Solutionvelocity time graph of a particle is shown in figure. Find displacement of the particle.
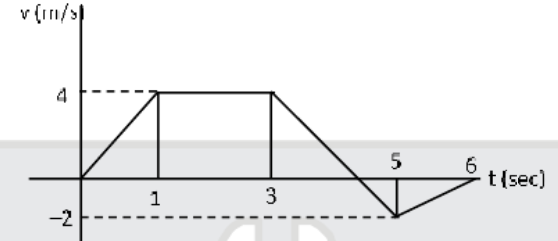
View SolutionThe velocity − time graph of a particle is as shown in figure

View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
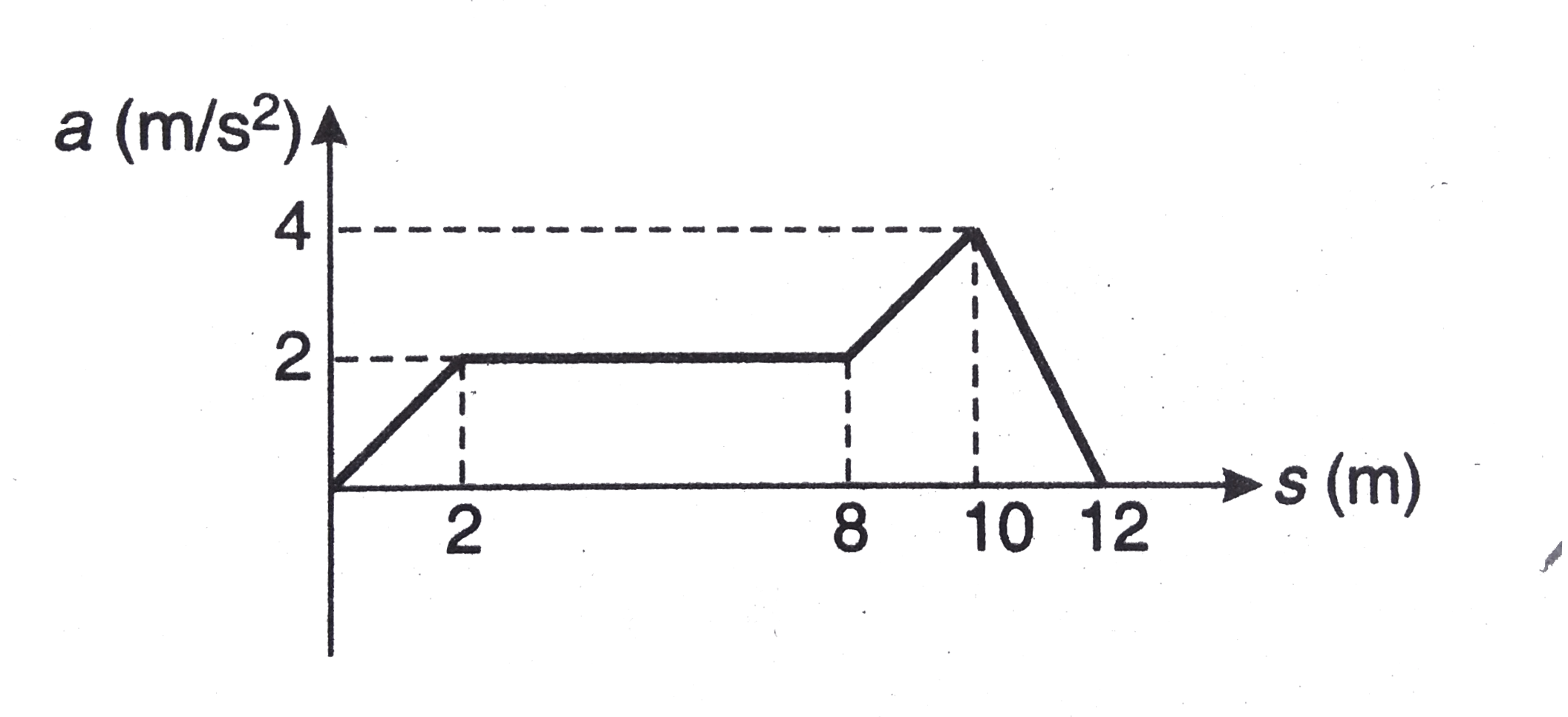
View SolutionReferring a−s diagram in the figure , find the velocity after particle travel 250m from starting. Assume v0=0.
 .
.
View SolutionThe displacement 'x' (in meter) of a particle of mass 'm' (in kg) moving in one dimension under the action of a force is released to time 't' (in sec) by t2=√x+2. The displacement of the particle when its velocity is zero will be.
View SolutionIf v=x2−5x+4, find the acceleration of the particle when velocity of the particle is zero.
View SolutionThe velocity of a particle is zero at t=0
View Solution
