If v=x2−5x+4, find the acceleration of the particle when velocity of the particle is zero.
0
2
3
none of these
The correct Answer is:A
v=0⇒x2−5x+4=0
x=1m&4m
dvdt=(2x−5)v=(2x−5)(x2−5x+4) at x=1m and 4m,dvdt=0
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp23
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 24
6 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 21
8 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Find the time t0 when x-coordinate of the particle is zero.
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View SolutionThe velocity of a particle moving along x-axis is given as v=x2−5x+4 (in m/s) where x denotes the x-coordinate of the particle in metres. Find the magnitude of acceleration of the particle when the velocity of particle is zero?
View SolutionA particle moves along the x-axis obeying the equation x=t(t−1)(t−2), where x is in meter and t is in second
a. Find the initial velocity of the particle.
b. Find the initial acceleration of the particle.
c. Find the time when the displacement of the particle is zero.
d. Find the displacement when the velocity of the particle is zero.
e. Find the acceleration of the particle when its velocity is zero.
View SolutionRefering to v−s diagram, find:
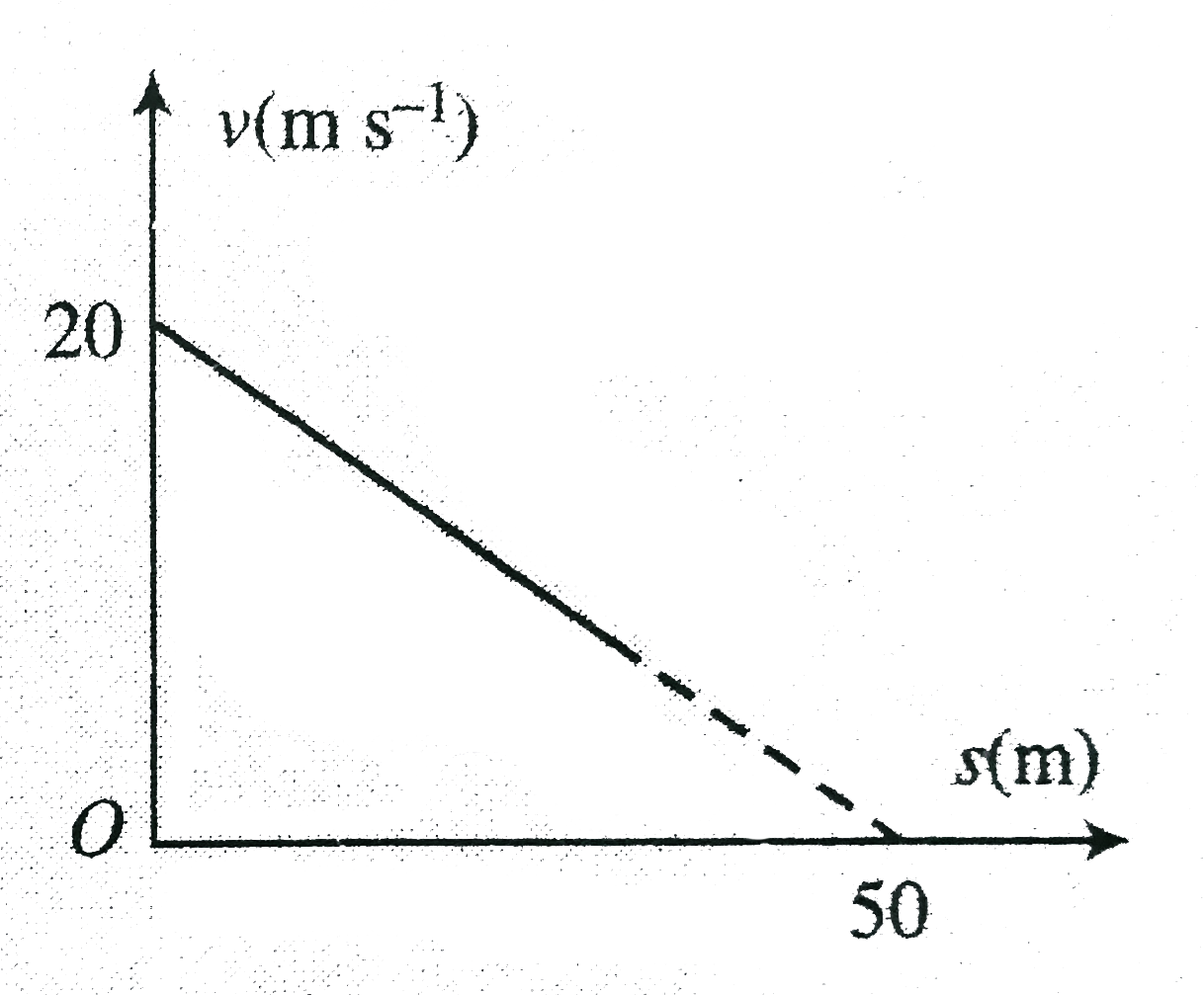 .
.
a. Acceleration of the particle when its velocity becomes half of the initial velocity.
b. Total distance covered by the particle.
View SolutionDisplacement-time equation of a particle moving along x-axis is x=20+t3−12t (SI units)
(a) Find, position and velocity of particle at time t=0.
(b) State whether the motion is uniformly accelerated or not.
(c) Find position of particle when velocity of particle is zero.
View SolutionDisplacement-time equation of a particle moving along x-axis is x=20+t3−12t (SI units)
(a) Find, position and velocity of particle at time t=0.
(b) State whether the motion is uniformly accelerated or not.
(c) Find position of particle when velocity of particle is zero.
View SolutionA particle moves in a straight line with a uniform acceleration a. Initial velocity of the particle is zero. Find the average velocity of the particle in first 's' distance.
View SolutionGive examples for the particle where (a) the velocity is in opposite direction to the acceleration (b)the velocity of the particle is zero but is acceleration is not zero.
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
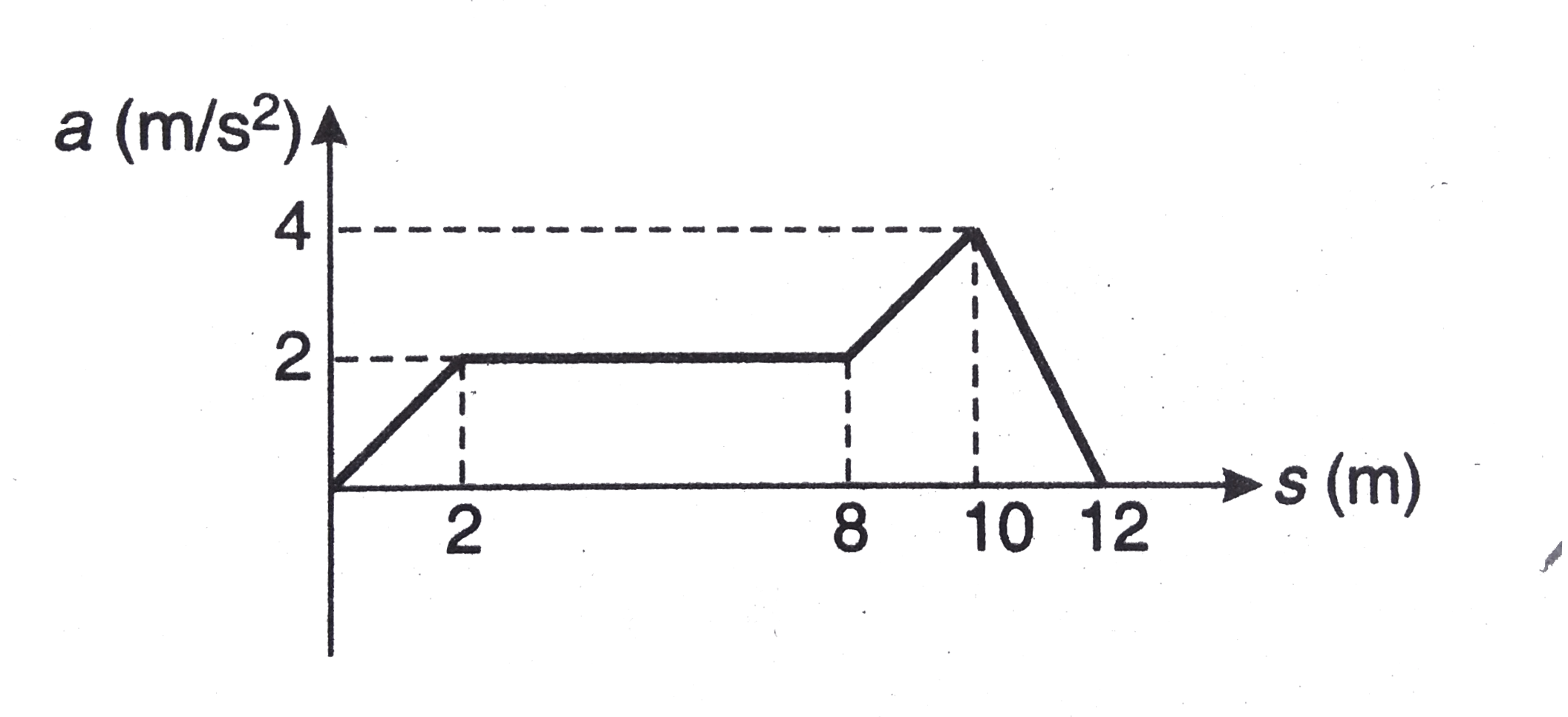
View Solution
