Seven homogeneous bricks, each of length L are arranged as shown in figure. Each brick is displaced with respect to the one in contact by L10. Find the x-coordinate of the centre of mass relative to the origin shown.
Solution in Tamil
Let 0(0,0)betheorignofthesystem.EachbrickisofmassMand≤n>hL,Eachbrickisdisplacedw.r.to≠∈contactbyL/10.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C09_E01_057_S01.pngwh=80%mx-autosty≤=background:white;><br>:. The X coordiN/Ate of the centre of mas Xcm
=1/{7mL/10)^((mL)/2+m(L/2+L/10)+.......+m(L/2)}/(7mL10)
Xcm=L2+L2+L10+L5+L2+3L10+L2+L5+L2+L10+L27
=7L2+5L10+2L57=22L35
Topper's Solved these Questions
Similar Questions
The centre of mass of a system of particles is at the origin. It follows that:
02:22View SolutionAn aluminium vessel of mass 0.5kg contains 0.2kg of water at 20∘C A block of iron of mass 0.2kgat100∘C is gently put into the water .Find the equilibrium temperature of the mixture, Specific heat capacities of aluminium , iron and water are 910Jkg−1K−1470Jkg−1K−1and4200Jkg−1K−1 respectively
04:54View SolutionFind the accelerationof the moon with respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution around the earth =27.3days
02:24View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l//4 and l//4 , respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.
08:36View SolutionFind the x coordinate of the centre of mass of the bricks shown in figure :
01:56View SolutionThree bricks each of length L and mass M are arranged as shown from the wall. The distance of the centre of mass of the system from the wall is
09:52View SolutionAn infinite no of bricks are placed one over the other as shown in the figure. Each succeeding brick having half the length and breadth of its precceeding brick and the mass of each succeeding bricks 1//4^(th) of the preceding one, take 'O' as the origin, the centre of mass of the system of bricks is at
07:14View SolutionInfinite rods of uniform mass density and length L,L/2,L/4….. Are placed one upon another upto infinite as shown in figure. Find the x-coordinate of centre of mass.
01:53View SolutionTwo identical bricks of length L are piled one on top of the other on a table as shown in the figure the maximum distance S the top brick can overhand the table with the system still balanced is:
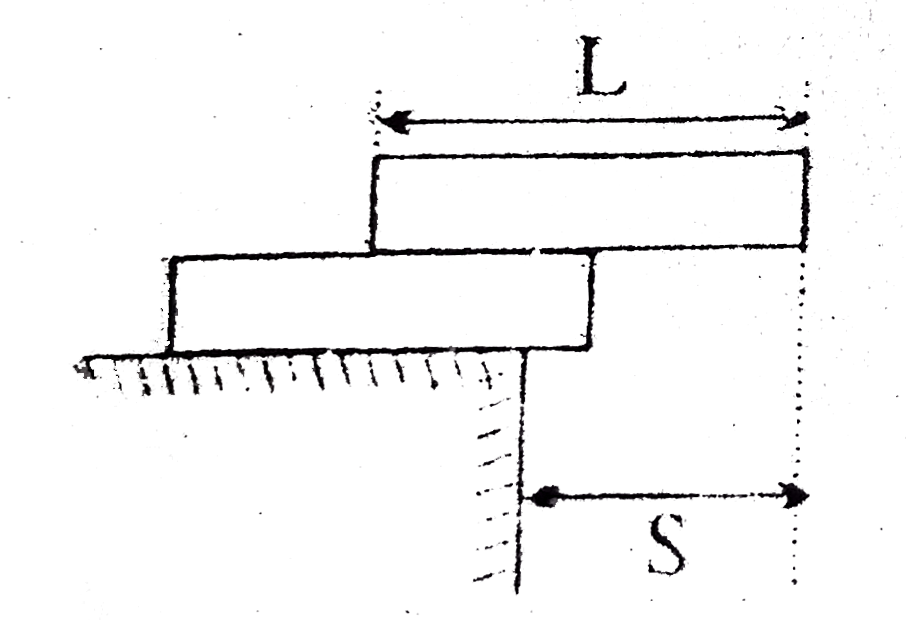11:35View SolutionInfinite number of bricks are placed one over the other as shown in the figure. Each succeeding brick having half the length and breadth of its preceding brick and the mass of each succeeding bricks being (1//4)^(th) of the preceding one. Taking 'O' as the origin, the x coordinate of centre of mass of the system of bricks is at
05:36View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O
01:56View Solutionसात समांगी (homogeneous) ईटे, जिनमें से प्रत्येक की लम्बाई L है , चित्र में दिखाए अनुसार सजाकर रखी गई है | प्रत्येक ईट अपने नीचे की ईट से L/10 दूरी खिसककर रखे गई है | चित्र में दिखाए गए मूलबिंदु O के अनुसार इस संहति के द्रव्यमान केंद्र का x-निर्देशांक बताएँ |
06:57View SolutionInfinite number of bricks are placed one over the other as shown in the figure. Each succeeding brick having half the length and breadth of its preceding brick and the mass of each succeeding bricks being (1//4)^(th) of the preceding one. Taking 'O' as the origin, the x coordinate of centre of mass of the system of bricks is at
08:27View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l/4andl/4, respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.
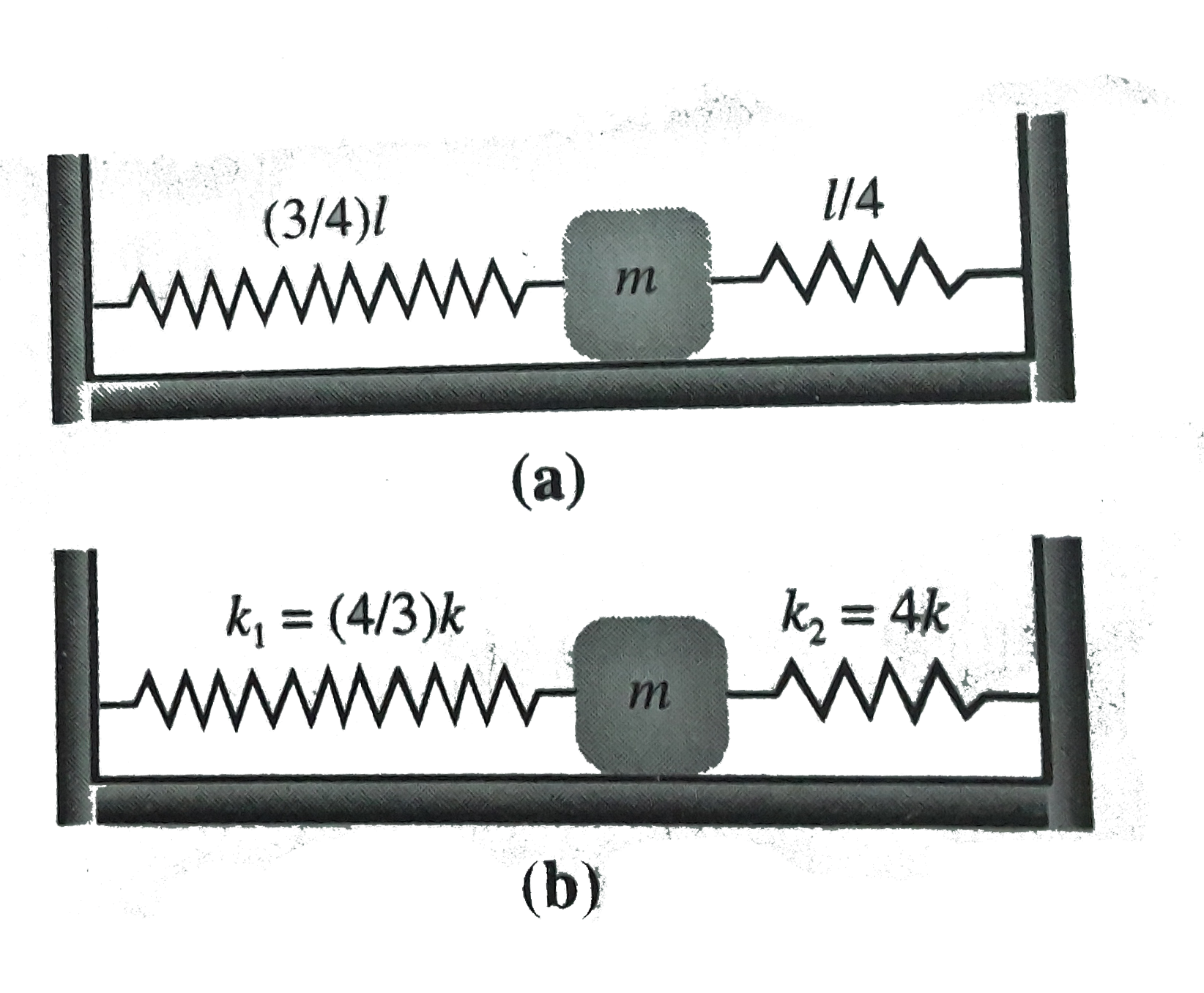04:56View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O
02:36View SolutionTwo identical bricks of length L are piled one on top of the other on a table as shown in the figure the maximum distance S the top brick can overhand the table with the system still balanced is:
02:10View Solution