An infinite no of bricks are placed one over the other as shown in the figure. Each succeeding brick having half the length and breadth of its precceeding brick and the mass of each succeeding bricks 1/4th of the preceding one, take 'O' as the origin, the centre of mass of the system of bricks is at

−a7
−5a7
−3a7
−2a7
The correct Answer is:3
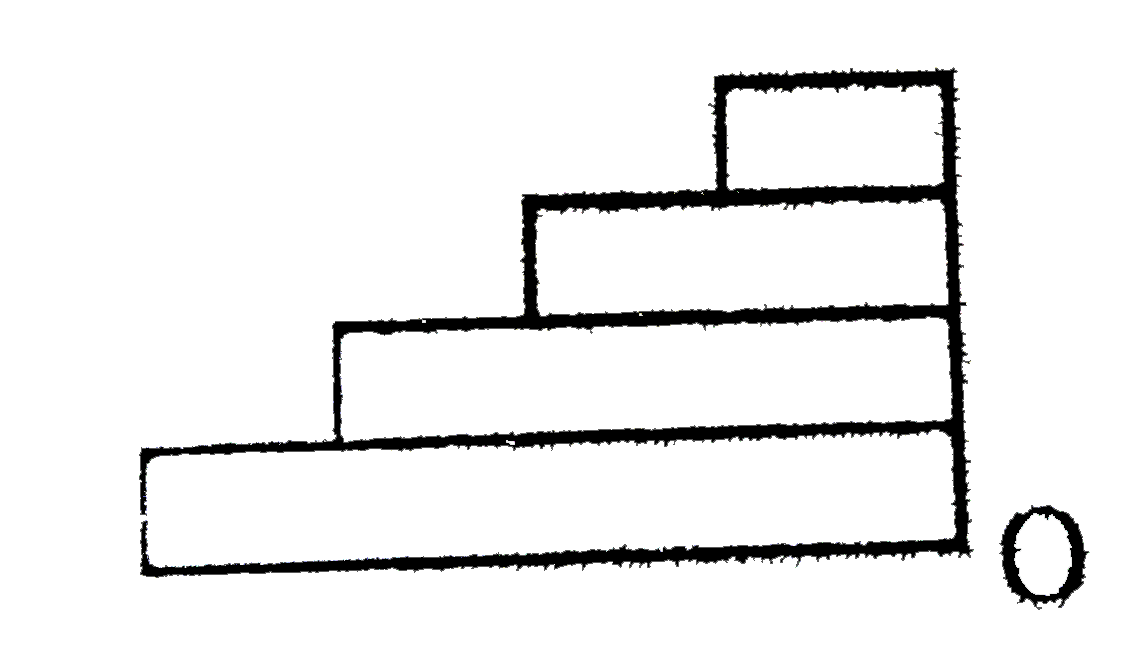
Xcm2=M1x1+M2x2+........M1+M2
=M(−a2)+M4(−a4)+M16(−a8)+......M+M4+M16+M64.........
[Ma2+Ma10+Ma128+.....][M+M4+M16+......]
M[a/21−(1/8)][(11−(1/4)])=−3a7
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
Three bricks each of length L and mass M are arranged as shown from the wall. The distance of the centre of mass of the system from the wall is
 View Solution
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Infinite number of bricks are placed one over the other as shown in the figure. Each succeeding brick having half the length and breadth of its preceding brick and the mass of each succeeding bricks being (1/4)th of the preceding one. Taking 'O' as the origin, the x coordinate of centre of mass of the system of bricks is at
 A−a/7B3a/7C−3a/7D−2a/7
A−a/7B3a/7C−3a/7D−2a/7 - Question 2 - Select One
Find the x coordinate of the centre of mass of the bricks shown in figure :
 A2425lB2524lC1516lD1615
A2425lB2524lC1516lD1615 - Question 3 - Select One
Two identical bricks of length L are piled one on top of the other on a table as shown in the figure the maximum distance S the top brick can overhand the table with the system still balanced is:
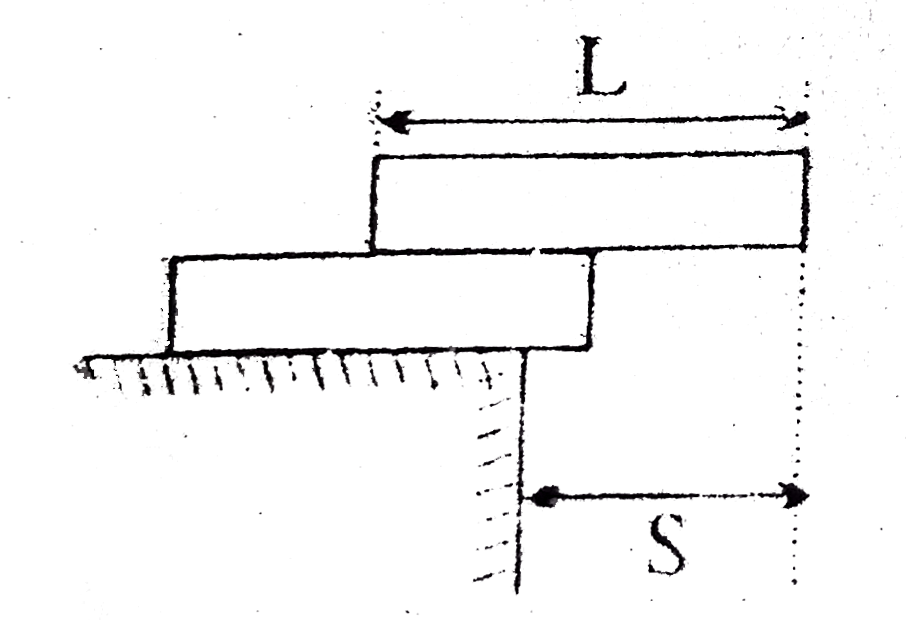 A12LB23LC34LD78L
A12LB23LC34LD78L
A square lamina of side a and a circular lamina of diameter a are placed touching each other as shown in figure. Find distance of their centre of mass from point O, the centre of sqaure.
 View Solution
View SolutionThree rods each of length L and mass M are placed along X, Y and Z axis in such a way that one end of each of the rod is at the origin. The moment of inertia of this system about Z axis is
View SolutionThe diagram shows 4 bricks enclosing a square. Each brick has length 18 cm and breadth 10 cm. Find the area enclosed (shaped) square.
View SolutionThere are 3 stair-steps as shown in the figure. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it if each brick is 12.5cm×6.25cm×4cm
View SolutionThree uniform thin rods, each of mass 1 kg and length √3\ m, are placed along three co-ordinate axes with one end at the origin. The moment of inertia of the system about X-axis is
View Solution

