Show a cylindrical tube of volume V_(0) divided in two parts by a frictionless separator. The walls of the tube are adiabatic but the separator is conducting, Ideal gases ate filled in the two parts. When the swparator is kept in the middle, the pressure are p_(1) and p-(2) in the left part and the right part respectively. The separator is slowly slid and is released at a position where it can stay in equilibrium. Find the volumes if the two parts. (figure)
As the separator is conducting, the tenperature is T when the separator is in the middle. Let n_(1) and n_(2) be the number of moles of the gas in the left part and the right part respectively. Using ideal gas equation,
p_(1)(v_(0))/(2)=n_(1)RT
and p_(2)(v_(0)=n_(2)RT.
Thus, (n_(1))/(n_(2))=p_(1)/p_(2) ...(i)
The separator will stay in equilibrium at a position wher the pressures on the two sides are equal. Suppose the volume of the left part is V_(1) and of the right part is V_(2) in this situation. Let the common pressure be p'. Also, let the common temperature in this situation be T'. Using ideal gas equation,
p'V1=n1RT'
and p'V2=n2RT'
or, V1V2=n1n2=p1p2 [using(i)]
Also, V1+V2=V0
Thus, V1=p1V0p1+p2 and V2=p2V0p1+p2.
Topper's Solved these Questions
- KINETIC THEORY OF GASESBOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Short Answer
14 Videos
- KINETIC THEORY OF GASESBOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Objective 1
17 Videos
- KINETIC THEORY OF GASESBOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Exercises
62 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises
19 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
Similar Questions
A cylindrical container of volume V0 is divided into two parts by a thin conducting separator of negligible mass. The walls of the container are adiabatic. Ideal gases are filled in the two parts such that the pressures are P0 and 2P0 when the separator is held in the middle of the container (see figure). Now the separator is slowly slid and released in a position where it stays in equilibrium. Find the volume of the two parts.
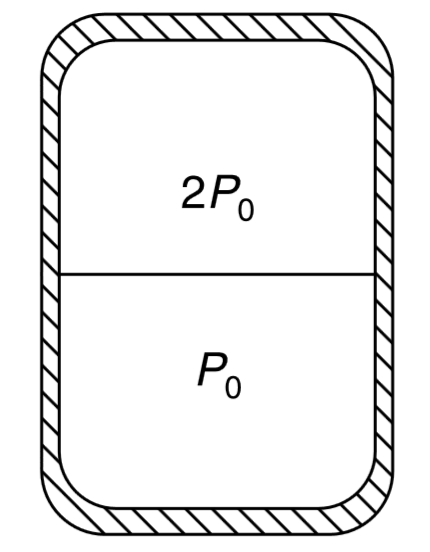
View SolutionIn given figure, an adiabatic cylindrical tube of volume 2V0 is divided in two equal parts by a frictionless adiabatic separator. An ideal gas in left side of a tube having pressure P1 and temperature T1 where as in the right side having pressure P2 and temperature T2.Cp/Cv=γ is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the final volumes of the two parts (b) the heat given to the gas in the left part and (c) the final common pressure of the gases,
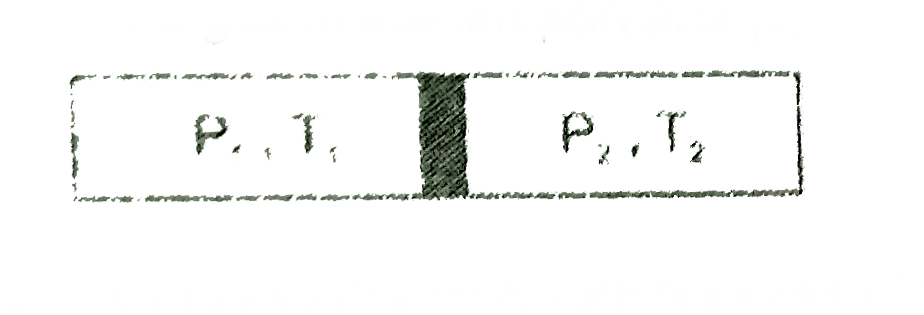
View Solution
Knowledge Check
Following figure shows on adiabatic cylindrical container of volume V0 divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (Cp/Cy=λ) is at pressure P and temperature T in left part and gas at pressure P and temperature T in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston)
 AP2BP1CP1(V02)λ(V02+Ax)λDP2(V02)λ(V02+Ax)λ
AP2BP1CP1(V02)λ(V02+Ax)λDP2(V02)λ(V02+Ax)λFallopian tube is part of
AUterusBUreterCVas deferensDOviduct.A block moving in air breaks in two parts and the parts separate
Athe total momentum must be conservedBthe total kinetic energy must be conservedCthe total momentum must changeDthe potential energy must be conserved
Figure shows an adiabatic cylindrical tube of volume (V0) divided in two parts by a frictionless adibatic separator . Initially, the separator is kept in the middle, an ideal gas at pressure (p1) and the temperatures (T1) is injected into the left part and the another ideal gas at pressures (P2) and temperature (T2) is injected into the right part. (CpCv=γ) is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the volumes of the parts, (b) the heat given to the gas in the left part and (c) the final common pressure of the gases.

View SolutionShows a cylindrical tube of length 30cm which is partitioned by a tight-fitting separator.The separator is very weakly conducting and can freely slide along the Tube. Ideal gases are filled in the two parts of the vessel. In the beginning, the temperature in the parts A and B are 400K and 100K respectively. The separator slides to a momentary equilibrium position of the separator,reached after a long time.

View SolutionA cylindrical tube of length 30 cm is partitioned by a tight-fitting separator. The separator is very thin, very weakly conducting and can freely slide along the tube. Ideal gases are filled in the two parts of the vessel. In the beginning, the temperature in the parts A and B are 400 K and 100 K respectively. The separator slides to a momentary equilibrium position at which the length of the tube at part A is 20 cm. Find the final equilibrium position of the separator, reached after a long time.
View SolutionA vertical cylinder closed at both ends is divided into two parts by a frictionless piston, each part containing one mole of air. At 300K the volume of the upper part is 4 times of the lower part. At what temperature will the volume of the upper part be three times that of the lower part?
View SolutionA vertical cylinder closed at both ends is divided into two parts by a frictionless piston, each part containing one mole of air. At 300K the volume of the upper part is 4 times of the lower part. At what temperature will the volume of the upper part be three times that of the lower part?
View Solution
