Show that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and and the inductor is constant in time.
To show that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and the inductor is constant in time, we can follow these steps:
Step 1: Write the expressions for energy stored in the capacitor and inductor.
The energy stored in the capacitor (E_C) is given by:
EC=Q22C
where Q is the charge on the capacitor and C is the capacitance.
The energy stored in the inductor (E_L) is given by:
EL=12LI2
where I is the current through the inductor and L is the inductance.
Step 2: Write the total energy in the circuit.
The total energy (E) in the LC circuit is the sum of the energies stored in the capacitor and the inductor:
E=EC+EL=Q22C+12LI2
Step 3: Express charge and current in terms of time.
In an LC circuit undergoing free oscillations, the charge Q on the capacitor varies with time as:
Q(t)=Q0sin(ωt)
where Q0 is the maximum charge and ω is the angular frequency.
The current I can be found by differentiating the charge with respect to time:
I(t)=dQdt=ddt(Q0sin(ωt))=Q0ωcos(ωt)
Step 4: Substitute expressions for Q and I into the total energy equation.
Substituting Q(t) and I(t) into the total energy equation:
E=(Q0sin(ωt))22C+12L(Q0ωcos(ωt))2
Step 5: Simplify the expression.
Now, substituting ω=1√LC:
E=Q20sin2(ωt)2C+12L(Q201LCcos2(ωt))
This simplifies to:
E=Q202Csin2(ωt)+Q202Ccos2(ωt)
Step 6: Factor out the common term.
Factoring out Q202C:
E=Q202C(sin2(ωt)+cos2(ωt))
Step 7: Use the Pythagorean identity.
Using the identity sin2(θ)+cos2(θ)=1:
E=Q202C⋅1=Q202C
Conclusion:
Thus, the total energy E is constant over time and is equal to Q202C. This shows that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and inductor is indeed constant in time.
---
The energy stored in the capacitor (E_C) is given by:
EC=Q22C
where Q is the charge on the capacitor and C is the capacitance.
EL=12LI2
where I is the current through the inductor and L is the inductance.
The total energy (E) in the LC circuit is the sum of the energies stored in the capacitor and the inductor:
E=EC+EL=Q22C+12LI2
In an LC circuit undergoing free oscillations, the charge Q on the capacitor varies with time as:
Q(t)=Q0sin(ωt)
where Q0 is the maximum charge and ω is the angular frequency.
I(t)=dQdt=ddt(Q0sin(ωt))=Q0ωcos(ωt)
Substituting Q(t) and I(t) into the total energy equation:
E=(Q0sin(ωt))22C+12L(Q0ωcos(ωt))2
Now, substituting ω=1√LC:
E=Q20sin2(ωt)2C+12L(Q201LCcos2(ωt))
This simplifies to:
E=Q202Csin2(ωt)+Q202Ccos2(ωt)
Factoring out Q202C:
E=Q202C(sin2(ωt)+cos2(ωt))
Using the identity sin2(θ)+cos2(θ)=1:
E=Q202C⋅1=Q202C
Thus, the total energy E is constant over time and is equal to Q202C. This shows that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and inductor is indeed constant in time.
Topper's Solved these Questions
Similar Questions
The energy stored in the capacitor in the steady state is
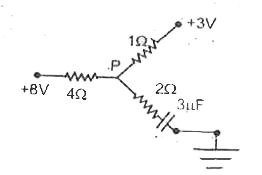 View Solution
View SolutionThe energy stored in 4μF capacitors is
View SolutionFind total energy stored in capacitors given in the circuit
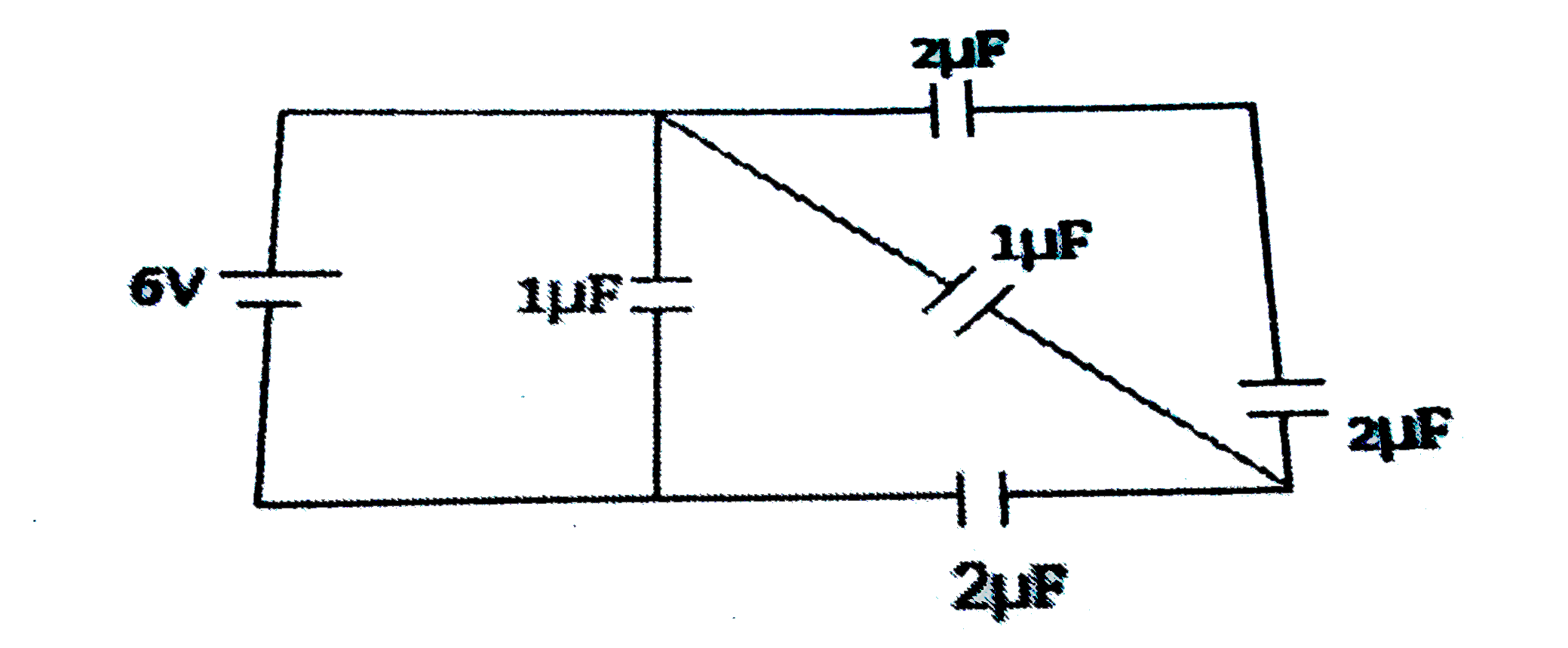 View Solution
View SolutionIn the circuit as shown in figure, energy stored in capacitor at steady state is
View SolutionFind the charge and energy stored on the capacitor C in the following circuit.
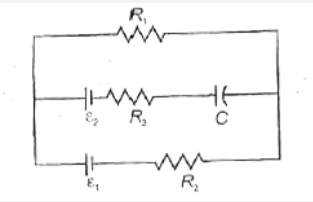 View Solution
View SolutionA 1.5μF capacitor is charged to 20 V. The charging battery is then disconnected , and a 15 mH coil is connected in series with the capacitor so that LC oscillations occur. Write the equation for variation of charge on capacitor and current in the inductor with time taking the instant at which inductor is connected to the capacitor as t=0.
View SolutionA 1.5μf capacitor is charged to 20 V. The charging battery is then disconnected and a 15 mH coil is connected in series with the capacitance so that LC oscillations occur. Write the equation for variation of charge on capacitor and current in the inductor with time taking at the instant at which inductor is connected to the capacitor at t = 0
View SolutionSwitch S is cloesd in the circuit at time t=0. Find the current through the capacitor and the inductor at any time t
 View Solution
View SolutionIn the circuit shown in fig. find the maximum energy stored on the capacitor. Initially, the capacitor was uncharged.
 View Solution
View SolutionConsider the given circuit.Initially there is no energy stored in inductor and capacitor.At
View Solution


