Suppose the circuit in Exercise 7.18 has a resistance of 15Ω Obtain the average power transferred to each element of the circuit, and the total power absorbed.
To solve the problem step by step, we will calculate the average power transferred to each element of the circuit and the total power absorbed.
Step 1: Identify the given values
- Resistance (R) = 15 Ω
- Inductance (L) = 80 mH = 80 × 10^(-3) H
- Capacitance (C) = 60 µF = 60 × 10^(-6) F
- Voltage (V) = 230 V
- Frequency (f) = 30 Hz
Step 2: Calculate the inductive reactance (X_L)
The formula for inductive reactance is:
XL=2πfL
Substituting the values:
XL=2π×30×(80×10−3)
XL=2π×30×0.08
XL≈15.08Ω
Step 3: Calculate the capacitive reactance (X_C)
The formula for capacitive reactance is:
XC=12πfC
Substituting the values:
XC=12π×30×(60×10−6)
XC=12π×30×0.00006
XC≈88.46Ω
Step 4: Calculate the impedance (Z) of the circuit
The impedance of the circuit is given by:
Z=√R2+(XL−XC)2
Substituting the values:
Z=√152+(15.08−88.46)2
Z=√225+(−73.38)2
Z=√225+5385.0644
Z≈√5610.0644
Z≈74.9Ω
Step 5: Calculate the root mean square (RMS) current (I)
The RMS current can be calculated using:
I=VZ
Substituting the values:
I=23074.9
I≈3.07A
Step 6: Calculate the average power absorbed by the resistor (P_R)
The average power absorbed by the resistor is given by:
PR=I2R
Substituting the values:
PR=(3.07)2×15
PR≈9.4249×15
PR≈141.37W
Step 7: Calculate the total power absorbed (P_total)
In this case, since we are only given the resistance, the total power absorbed is the same as the power absorbed by the resistor:
Ptotal=PR
Ptotal≈141.37W
Final Result
- Average power transferred to the resistor (P_R) = 141.37 W
- Total power absorbed (P_total) = 141.37 W
- Resistance (R) = 15 Ω
- Inductance (L) = 80 mH = 80 × 10^(-3) H
- Capacitance (C) = 60 µF = 60 × 10^(-6) F
- Voltage (V) = 230 V
- Frequency (f) = 30 Hz
The formula for inductive reactance is:
XL=2πfL
Substituting the values:
XL=2π×30×(80×10−3)
XL=2π×30×0.08
XL≈15.08Ω
The formula for capacitive reactance is:
XC=12πfC
Substituting the values:
XC=12π×30×(60×10−6)
XC=12π×30×0.00006
XC≈88.46Ω
The impedance of the circuit is given by:
Z=√R2+(XL−XC)2
Substituting the values:
Z=√152+(15.08−88.46)2
Z=√225+(−73.38)2
Z=√225+5385.0644
Z≈√5610.0644
Z≈74.9Ω
The RMS current can be calculated using:
I=VZ
Substituting the values:
I=23074.9
I≈3.07A
The average power absorbed by the resistor is given by:
PR=I2R
Substituting the values:
PR=(3.07)2×15
PR≈9.4249×15
PR≈141.37W
In this case, since we are only given the resistance, the total power absorbed is the same as the power absorbed by the resistor:
Ptotal=PR
Ptotal≈141.37W
- Average power transferred to the resistor (P_R) = 141.37 W
- Total power absorbed (P_total) = 141.37 W
Topper's Solved these Questions
Similar Questions
An AC circuit containing 800mH inductor and a 60μF capacitor is in series with 15Ω resistance. They are connected to 230 V ,50 Hz AC supply. Obtain average power transferred to each element and total power absorbed.
View SolutionFor the given circuit,
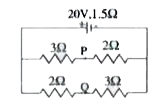
If internal resistance of cell is 1.5Ω, then
View SolutionA series AC circuit has a resistance of 4Ω and a reactance of 3Ω. The impedance of the circuit is
View SolutionA series AC circuit has a resistance of 4Ω and a reactance of 3Ω. The impedance of the circuit is
View SolutionA circuit containing an 80mH inductor and a 60μF capacitor in series is connected to a 230V−50Hz Supply. The resistance in the circuit is negligible .
(a) Obtain the current amplitude and rms currents.
(b) Obtain the rms values of voltage across inductor and capacitor.
(c ) What is the average power transferred to the inductor and to the capacitor?
(d) What is the total power absorbed by the circuit?
View Solution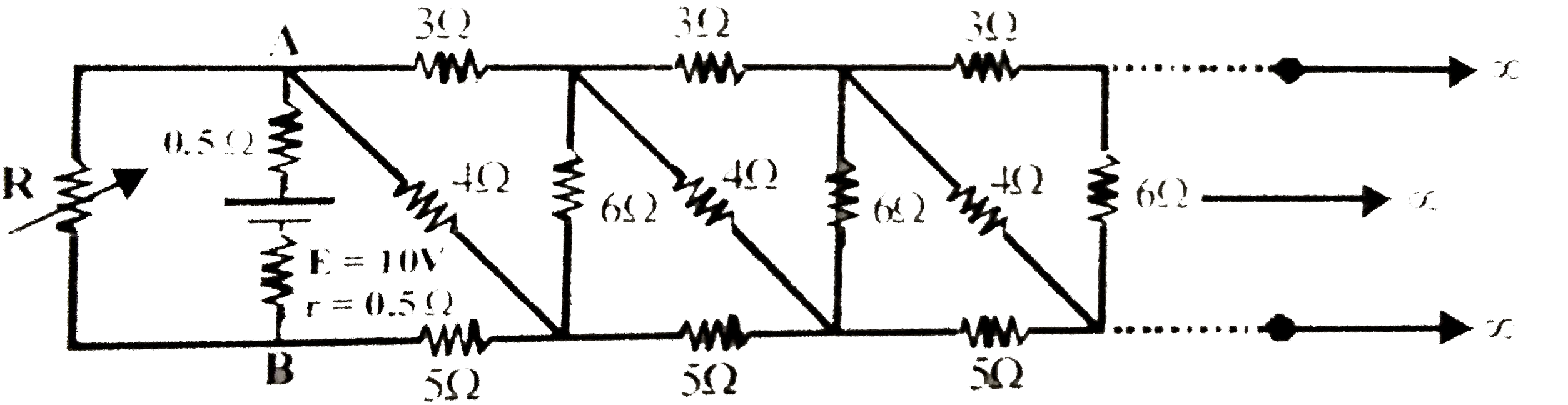
Maximum power transfer to external circuit in watt will be
View SolutionFind the average power consumed in the circuit consisting of resistanceless inductor .
View SolutionA circuit has a resistance of 12 ohm and an impendance of 15 ohm. The power factor of the circuit will be
View SolutionA series L-C-R circuit with R = 20Ω, L = 1.5 H and C =35μF is connected to a variable frequency 200 V, AC supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transfered to the circuit, what is the average power transfered to the circuit in one complete cycle ?
View Solution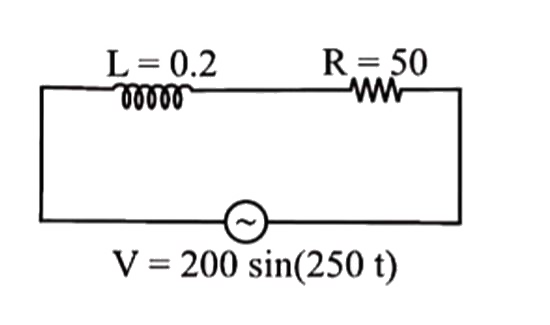
In the given circuit the average power developed is:
View Solution
