Show that the angular momentum about any point of a single particle moving with constant velocity remains constant throughout the motion.
To show that the angular momentum about any point of a single particle moving with constant velocity remains constant throughout the motion, we can follow these steps:
Step 1: Define the Angular Momentum
The angular momentum L of a particle about a point O is given by the formula:
L=r×p
where r is the position vector from point O to the particle, and p is the linear momentum of the particle.
Step 2: Express the Linear Momentum
The linear momentum p of the particle can be expressed as:
p=mv
where m is the mass of the particle and v is its velocity. Since the particle is moving with constant velocity, both m and v are constants.
Step 3: Analyze the Position Vector
Let r be the position vector from point O to the particle at any time t. The particle moves along a straight line with constant velocity v, so:
r(t)=r0+vt
where r0 is the initial position vector of the particle at t=0.
Step 4: Calculate the Angular Momentum
Substituting p into the angular momentum formula, we have:
L=r×(mv)=m(r×v)
This shows that the angular momentum depends on the cross product of the position vector r and the constant velocity vector v.
Step 5: Analyze the Cross Product
The magnitude of the angular momentum can be expressed as:
|L|=m|r||v|sinθ
where θ is the angle between r and v.
Step 6: Show that Angular Momentum is Constant
As the particle moves, the position vector r changes, but the distance from point O to the line of motion (which is |r|sinθ) remains constant. This is because the particle is moving in a straight line with constant velocity. Therefore, the product |r|sinθ remains constant.
Conclusion
Since both m and |v| are constants, and |r|sinθ is also constant, we conclude that the angular momentum L remains constant throughout the motion:
L=m|v|(|r|sinθ)=constant
The angular momentum L of a particle about a point O is given by the formula:
L=r×p
where r is the position vector from point O to the particle, and p is the linear momentum of the particle.
The linear momentum p of the particle can be expressed as:
p=mv
where m is the mass of the particle and v is its velocity. Since the particle is moving with constant velocity, both m and v are constants.
Let r be the position vector from point O to the particle at any time t. The particle moves along a straight line with constant velocity v, so:
r(t)=r0+vt
where r0 is the initial position vector of the particle at t=0.
Substituting p into the angular momentum formula, we have:
L=r×(mv)=m(r×v)
This shows that the angular momentum depends on the cross product of the position vector r and the constant velocity vector v.
The magnitude of the angular momentum can be expressed as:
|L|=m|r||v|sinθ
where θ is the angle between r and v.
As the particle moves, the position vector r changes, but the distance from point O to the line of motion (which is |r|sinθ) remains constant. This is because the particle is moving in a straight line with constant velocity. Therefore, the product |r|sinθ remains constant.
Since both m and |v| are constants, and |r|sinθ is also constant, we conclude that the angular momentum L remains constant throughout the motion:
L=m|v|(|r|sinθ)=constant
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT ENGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE
33 Videos
- PHYSICAL WORLD BOOK - NCERT ENGLISHCHAPTER - PHYSICAL WORLD EXERCISE - EXERCISE
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE
22 Videos
Similar Questions
Knowledge Check
Angular momentum of the particle rotating with a central force is constant due to
Aconstant torqueBconstant forceCconstant linear momentumDzero torque
What is the angular acceleration of a particle moving with constant angular velocity ?
View SolutionWhich of the following graphs represents the motion of a particle moving with constant velocity?
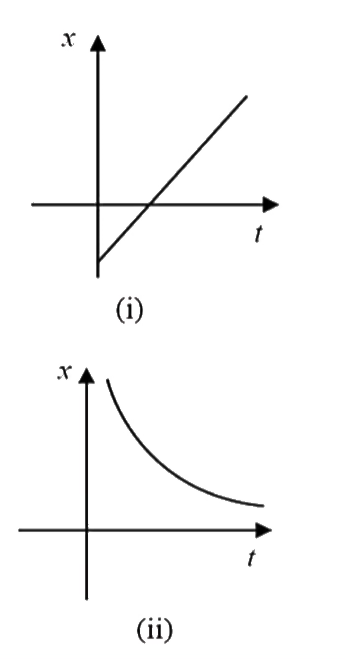
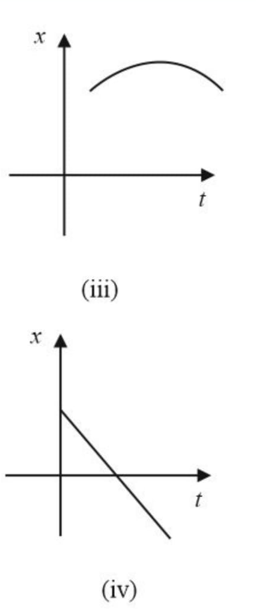
View SolutionAssertion: If linear momentum of a particle is constant, then its angular momentum about any point will also remain constant.
Reason: Linear momentum remains constant if Fnet=0 and angular momentum remains constant if τnet=0
View SolutionAssertion : Distance between two particles moving with consant velocities always remains constant.
Reason : In the above case, relative motion between them is uniform.
View SolutionWhat is the torque acting on a body moving with constant angular velocity ?
View SolutionWhat is the torque acting on a body moving with constant angular velocity ?
View SolutionAssertion : A body is moving along a circle with a constant speed. Its angular momentum about the centre of the circle remains constant
Reason : In this situation, a constant non-zero torque acts on the body.
View Solution
