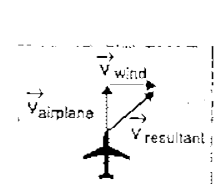
Similarly if an airplane moves in a wind its resultant velocity will be a conbination of its own velocity and velocity of wind.
→vresultant=→vairplane+→vwind
(1).

Vectors to be added are placed tail such that they represent consecutive sides of a parallelogram. Diagonal of parallelogeam represent resultant.
Step by step video & image solution for Similarly if an airplane moves in a wind its resultant velocity will be a conbination of its own velocity and velocity of wind. vecv_("resultant")=vecv_("airplane")+vecv_("wind") (1). Vectors to be added are placed tail such that they represent consecutive sides of a parallelogram. Diagonal of parallelogeam represent resultant. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Assertion : An object has given two velocities →v1 and →v2 has a resultant velocity →v=→v1+→v2.
Reason : →v1and→v2 should be velocities with reference to some common reference frame.
View SolutionA particle tied to a string moves in a circular path in vertical plane. Its velocity at lowerst point is such that it just completes circle. Find the ratio of resultant force on particle at the lowerst point to that at highest point.
View Solution
Knowledge Check
We know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
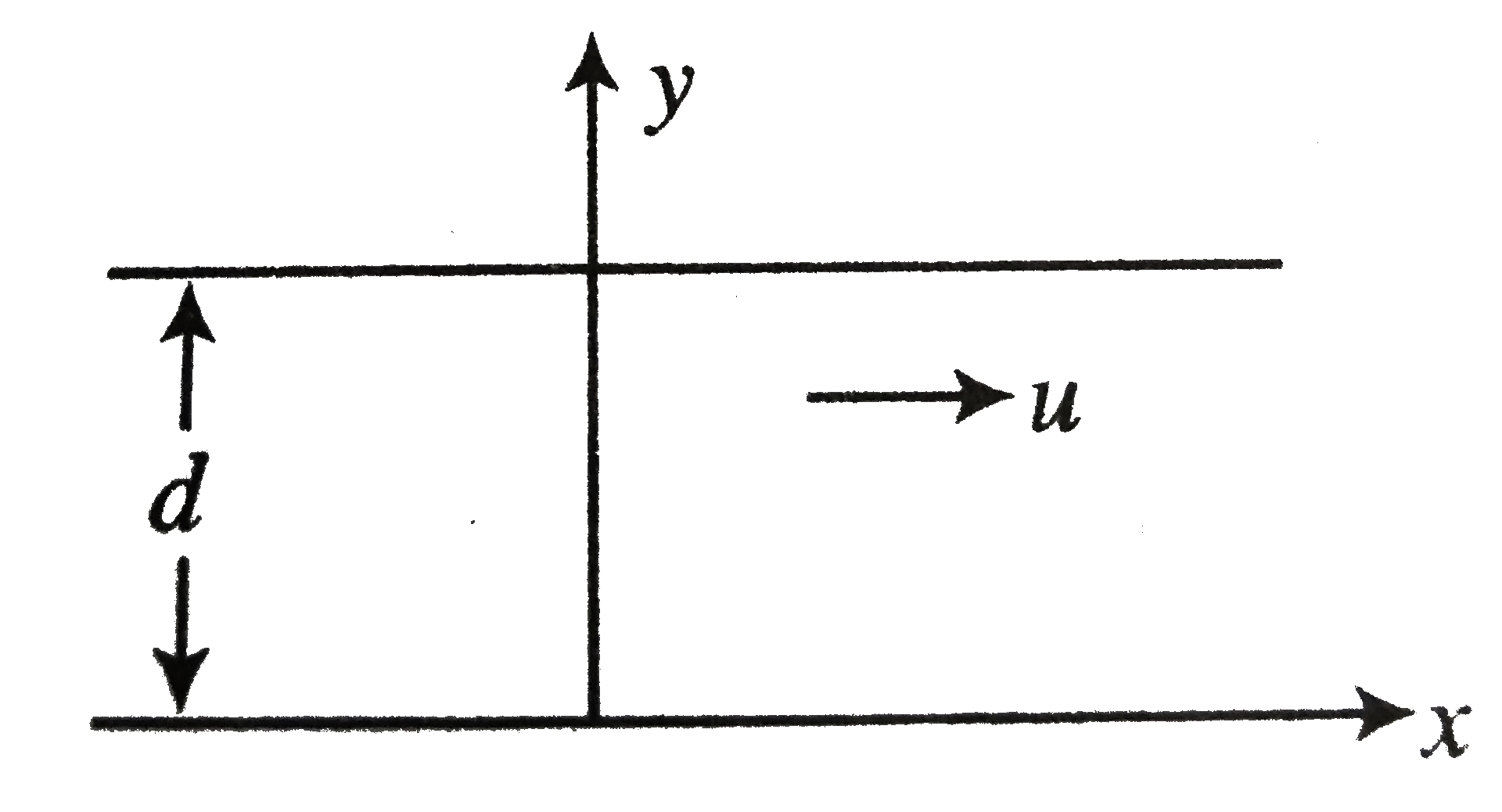
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.A(3d/5)1/3B(6d/5)1/3C(6d/5)1/2D(2d/3)1/3We know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
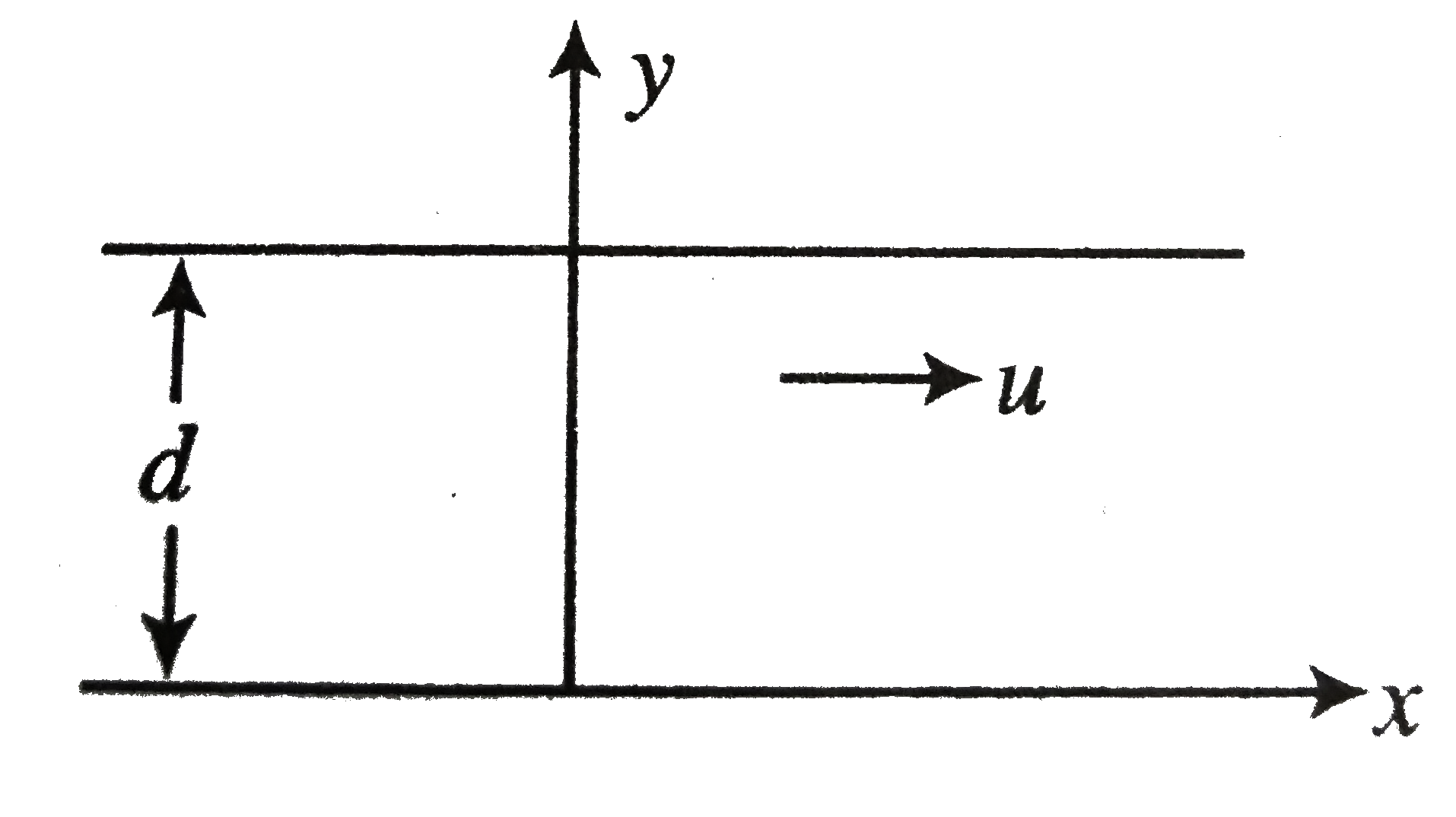
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.Ax−1=u(3y5)1/3Bx=u(6y5)1/3Cx=1=u(6y5)1/3DNone of theseWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.Au(3d5)1/3Bu(3d5)1/3 + 1Cu(6d5)1/3DNone of these
Figure shows top view of an airplane blown off course by wind in various directions. Assume the magnitude of the velocity of the airplane relative to the wind and the magnitude of the velocity of the wind to be the same each case. →vA/w=velocity of the airplane relative to the wind, →vw/g= velocity of the wind in ground frame
View SolutionThe vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If →vAis the absolute velocity of a body A and →–––(B)that of another body B then the relative velocity of A in relation to B is →–––(AD)=→VA−→vB and →vBA=→vB-→vA.
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A train A moves to the east with velocity of 40 km/hr and a train B moves due north with velocity of 30 km/hr. The relative velocity of A w.rt. B is
View SolutionThe vector difference between the absolute velocities of two bodies is called their relative velocity. The concept of relative velocity enables us to treat one body as being at rest while the other is in motion with the relative velocity. This jormalism greatly simplifies many problems. If →vAis the absolute velocity of a body A and →–––(B)that of another body B then the relative velocity of A in relation to B is →–––(AD)=→VA−→vB and →vBA=→vB-→vA.
The principle follows here is that the relative velocity of two bodies remains unchaged if the same additional velocity is imparted to both the bodies. A simple way of carrying out this operation is to be represent the velocities in magnitude and direction from a common point. Then the line joining the tips of the vectors represents the relative velocity
Q A river is flowing from west to east at a speed of 5 m/s. A man on the south bank of the river, capable of swimming at 10 m/s in still water, wants to cross the river without drifting, he. should swim
View SolutionAn electron is moving with an initial velocity →v=v0ˆi and is in a magnetic field →B=→B0ˆj. Then its de-Broglie wavelength
View SolutionSuppose that two objects A and B are moving with velocities →vA and →vB (each with respect to some common frame of refrence). Let →vAB represent the velocity of A with respect to B. Then
View Solution
