Solve the previous problem if the firction coefficient between the 2.0 kg block and the plane below it is 0.5 and the plane below the 4.0 kg block is frictionless.
The correct Answer is:A, B
m1=4,m2=2kg
FricitoN/Al coefficient between 2 kg block
and surface =0.5
R=10 cm=0.1m<br>I=0.5kg-m^2<br>-m_1gsintheta-T_1<br>=m1a…..1
−T2−(m2gsinθ+μm2gcosθ)
=m2a…2
(T1−T2)=Iar2……3
Adding equation 1 and 2 we will get
m1gsinθ−(m2gsinθ−μmgcosθ)+(T2−T1)
=ma+m2a
=4×9.8×91√2)<br>{2xx9.8xx(1/sqrt2)+0.5xx2xx9.8xx(1/sqrt2)}<br>=(4+2+05/0.01)a<br>rarr 37.80-(13.90+6.95)=56a<br>rarr 27.8-20.3=56a<br>rarr a=7/56=0.125m/s^2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
In Fig. 6-52, two blocks, in contact, slide down an inclined plane AC of inclination 30∘ . The coefficient of kinetic friction between the 2.0 kg block and the incline is u1=0.20 and that between the 4.0 kg block and the incline is μ2=0.30. Find the magnitude of the acceleration.

View SolutionFigure shows tow blocks in contact sliding down an inclined surface of inclination 300. The friction coefficient between the block o fmass 2.0 kg and the incline is μ1 and that between the block of mas 4.0 kg and the incline is μ2. Calculate teh acceleration of the 2.0 kg bloc if a. μ1=0.20andμ2=0.30b.μ1=0.30andμ2=0.20.Take g=10ms2.

View Solution
Knowledge Check
In the arrangement shown in figure coefficient of friction between 5kg block and incline plane is μ=0.5. Friction force acting on the 5kg block is
 A20NB15NC10ND5N
A20NB15NC10ND5NA block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ1kg and 4kg blocks lie on a rough horizontal surface. The coefficient of friction between 4kg blocks and surface is 0.2 while the coefficient of firction between 1kg blocks and the surface is 0.6. All the pulley shown in the figure are massless and frictionless and all strings are massless and frictionless and all strings are massless.
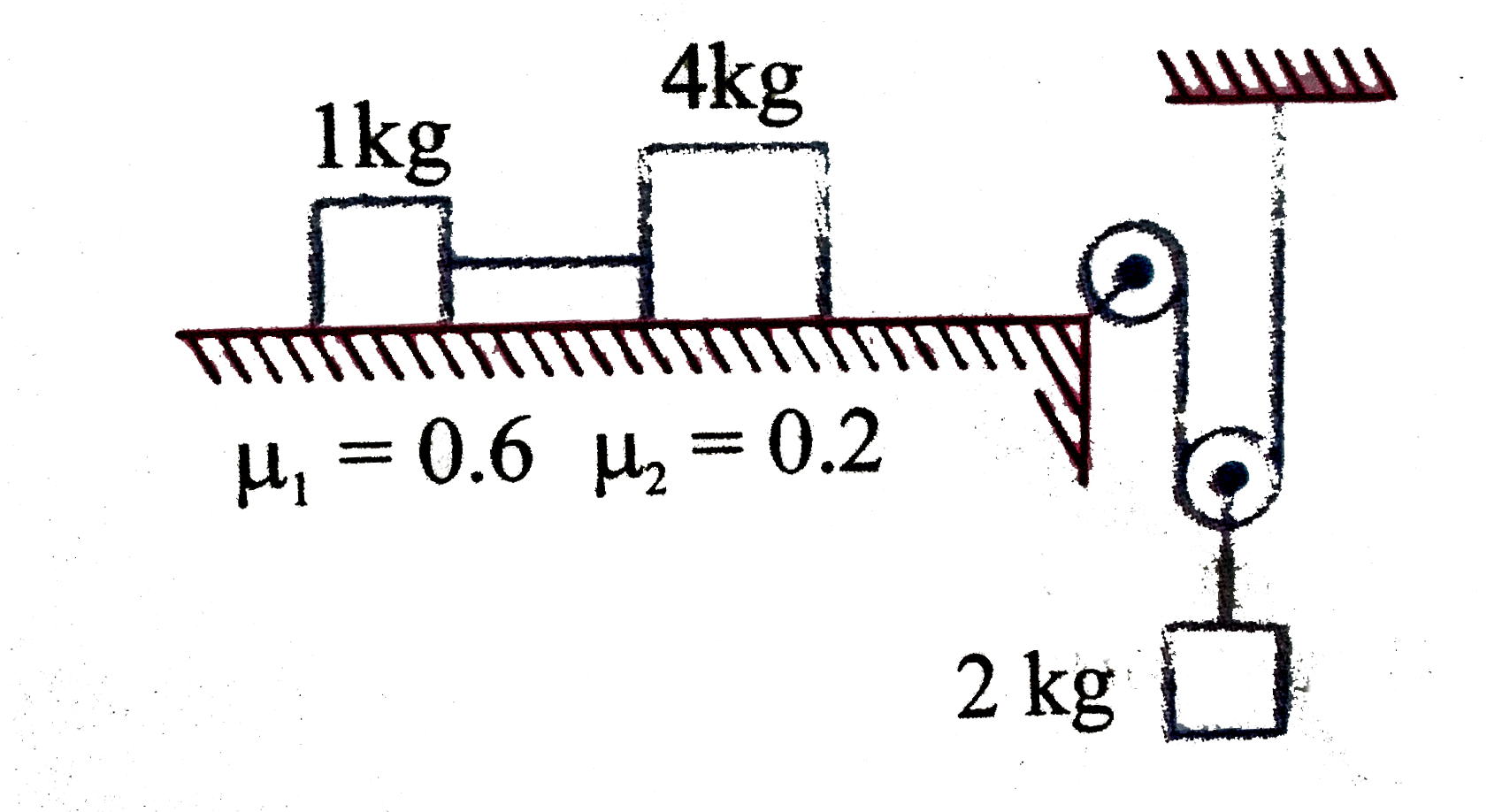 AThe frictional force acting on 1kg blocks is 2N.BThe frictional force acting on 1kg block is 6NCThe tension in the string connecting 4kg block and 1kg blocks is 1NDThe tension in the string connecting 1kg block and 4kg blocks is zero.
AThe frictional force acting on 1kg blocks is 2N.BThe frictional force acting on 1kg block is 6NCThe tension in the string connecting 4kg block and 1kg blocks is 1NDThe tension in the string connecting 1kg block and 4kg blocks is zero.
A block of mass 5 kg is pulled along a horizontal. The friction coefficient between the block and the surface is 0.5. If the block travels at constant velocity, find the work done by this applied force during a displacement 4 m of the block.
View SolutionA block of mass 1kg is pressed against a wall by applying a horizontal force of 10N on the block. If the coefficient of friction between the block and the wall is 0.5 ,magnitude of the frictional force acting on the block is
View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View SolutionA block of mass 0.1 kg is held against a wall by applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, then the magnitude of the frictional force acting on the block is
View SolutionA force of 750 N is applied to a block of mass 102 kg to prevent it from sliding on a plane with an inclination angle 30∘ with the horizontal. If the coefficients of static friction and kinetic friction between the block and the plane are 0.4 and 0.3 respectively, then the frictional force acting on the block is
View Solution
