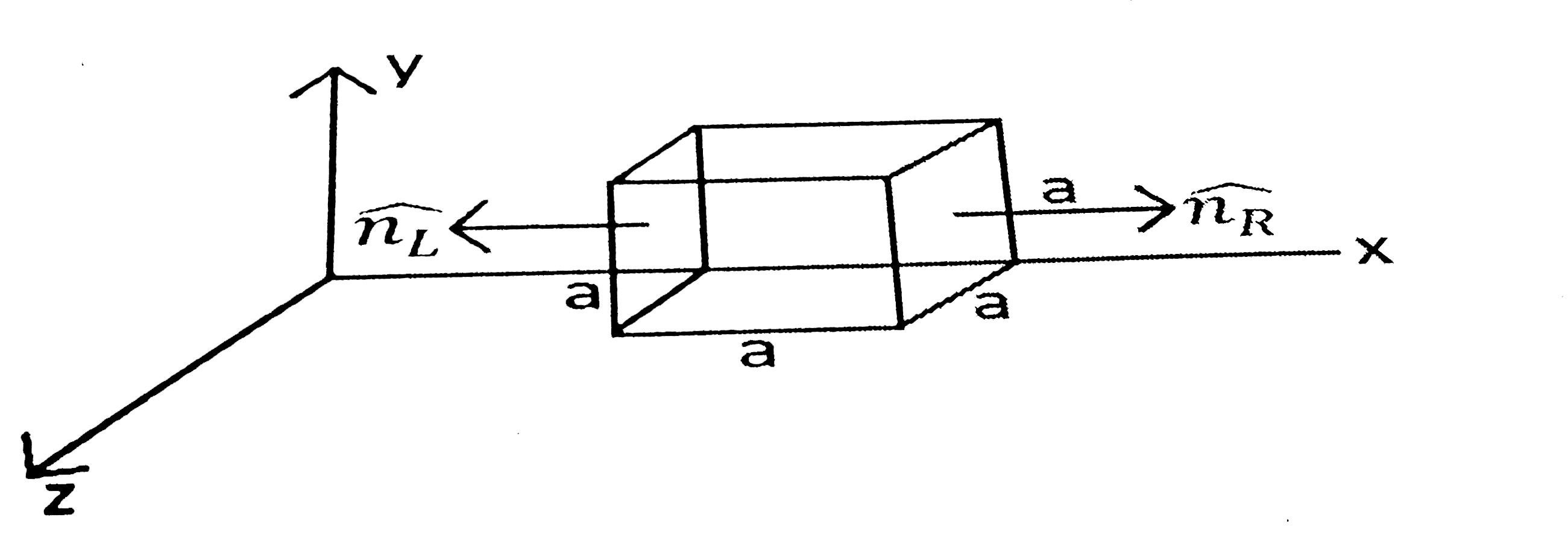
State Gauss’s law in electrostatics. A cube with each side a is kept in an electric field given by E = Cx (as shown in the figure) where C is a positive dimensional constant. Find out :
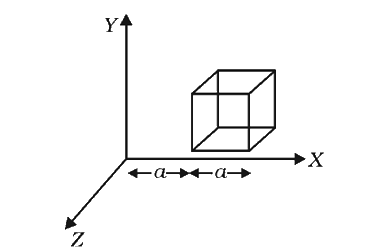
(i) The electric flux through the cube (ii) The net charge inside the cube.
Gauss’s law states that the total electric flux through a closed surface is equal to 1e0 times the magnitude of the charged by enclosed by it.
ϕ=e∠0
Here, e0 is the absolute permittivity of the free space and q is the total charge enclosed.
Also ϕ=∫E.ds=qE0
Where, E is the electric field at the area element dS. Now, the electric field is in X-direction only. So, face with surface normal vector perpendicular to this field would give zero electric flux i.e.,
ϕ=Edscos90∘=0 through it.
So, flux would be across only two surfaces
Magnitude of E at left face ,
EL=Cx=Ca[x=a at left face]
Magnitude of E at right face
ER=Cx=C2a=2aC[x=2a right face]
Thus, corresponding fluxes are
ϕ=El.ds=ELdscos180∘=−ac×a2=−a3c,ϕR=ER.ds=2acDccos0∘=2aca2=2a3C
(i)Now, net flux through cube =ϕL+ϕR=−a3C+2a3C=a3CNm2C−1
(ii) We have, ϕ=ee0ore=ϕe0,Q=a3Ce0 Coulomb
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 0 (LONG ANSWER TYPE )
8 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 1
105 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Videos
Similar Questions
A cube of side 1 is placed in a uniform field E, where E=Eˆi. The net electric flux through the cube is
View SolutionA hemispherical surface of radius R is kept in a uniform electric field E as shown in figure. The flux through the curved surface is

View SolutionIn figure +Q charge is located at one of the edge of the cube as shown in figure-1.376. Then electric flux through cube due to +Q charge is given as

View SolutionA cube has sides of length L. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=−Bˆi+Cˆj−Dˆk, where B, C and D are positive constants.
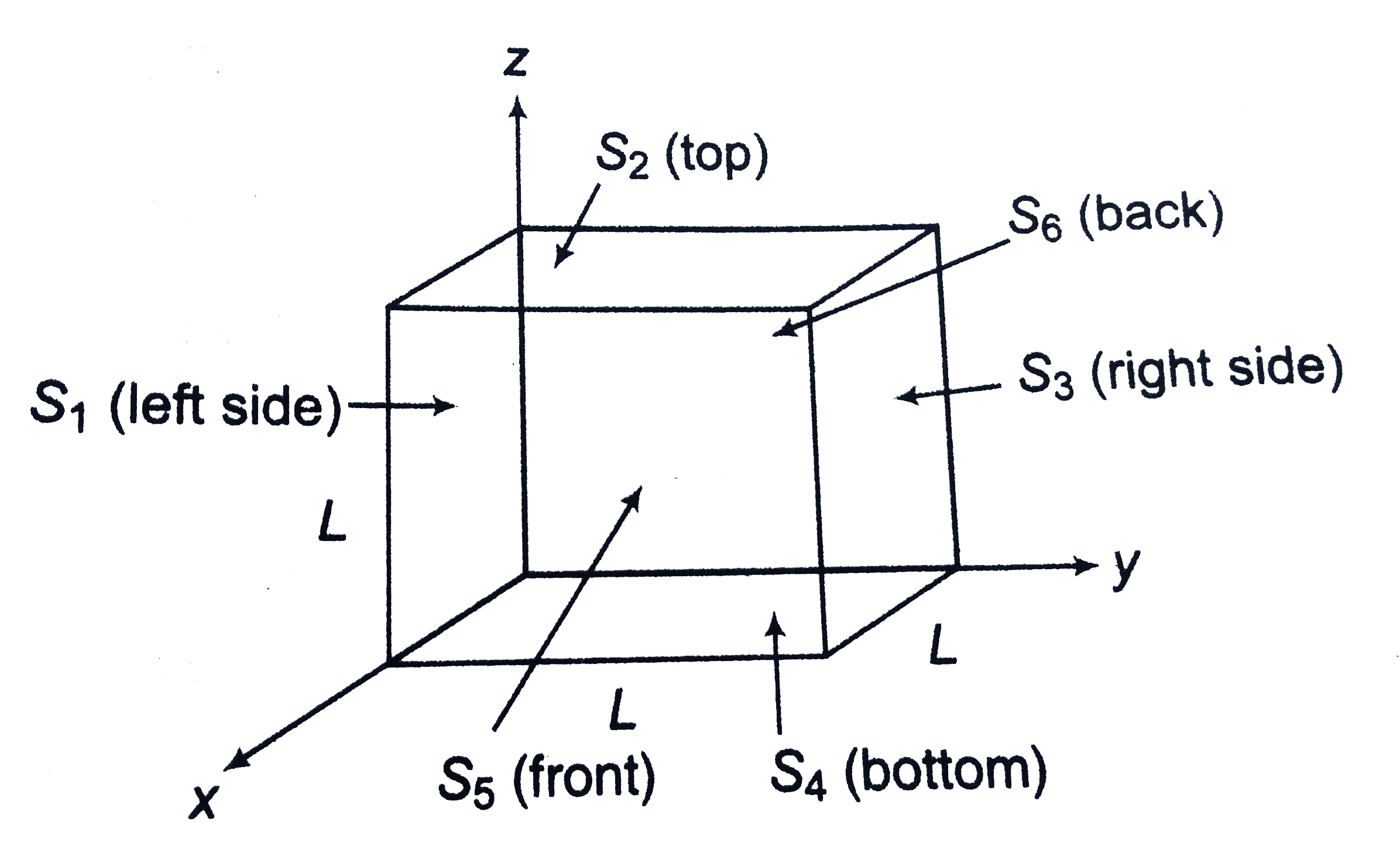
(a) Find the electric flux through each of the six cube faces S1,S2,S3,S4andS5andS6.
(b) Find the electric flux through the entire cube.
View SolutionA charge +Q is placed on middle of edge of the cube.Then electric flux through cube due to field of charge +Q is
View SolutionA charge q is placed at point D of the cube. Find the electric flux passing through the EFGH and face AEHD.

View SolutionA charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaced of the cube.
View SolutionCharge of 2 C is placed at the centre of a cube. What is the electric flux passing through one face ?
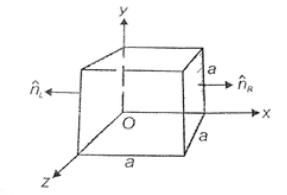
View SolutionThe electric field components in the figure below are Ex=800x2N/C,Ey=Ez=0.
Calculate
(1) The flux throught he cube and
(2) The charge withing the cube
Assume that a =0.1 m
View SolutionUsing Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
View Solution
