State Ohm's law. Derive an expression for the equivalent resistance of a number of resistances in parallel.
Step-by-Step Solution:
Step 1: State Ohm's Law
Ohm's Law states that the current (I) flowing through a conductor between two points is directly proportional to the voltage (V) across the two points, provided the temperature remains constant. Mathematically, it can be expressed as:
V=I×R
where R is the resistance of the conductor.
Step 2: Define Resistance
Resistance (R) is defined as the opposition offered by a material to the flow of electric current. It can be calculated using the formula:
R=VI
Step 3: Understanding Resistors in Parallel
When resistors are connected in parallel, the voltage across each resistor is the same, but the total current flowing through the circuit is the sum of the currents flowing through each resistor.
Step 4: Deriving the Expression for Equivalent Resistance in Parallel
Let’s consider n resistors R1,R2,R3,…,Rn connected in parallel. The voltage across each resistor is the same, denoted as V.
The current through each resistor can be expressed using Ohm’s Law:
- For R1: I1=VR1
- For R2: I2=VR2
- For R3: I3=VR3
- ...
- For Rn: In=VRn
The total current I flowing into the parallel combination is the sum of the individual currents:
I=I1+I2+I3+…+In
Substituting the expressions for I1,I2,…,In:
I=VR1+VR2+VR3+…+VRn
Step 5: Factor out the Voltage (V)
Factoring V out of the equation:
I=V(1R1+1R2+1R3+…+1Rn)
Step 6: Relate Total Current to Equivalent Resistance
By Ohm's Law, we can also express the total current in terms of the equivalent resistance Req:
I=VReq
Step 7: Equate the Two Expressions for Current
Setting the two expressions for current equal to each other:
VReq=V(1R1+1R2+1R3+…+1Rn)
Step 8: Simplify to Find Equivalent Resistance
Dividing both sides by V (assuming V≠0):
1Req=1R1+1R2+1R3+…+1Rn
Thus, the expression for the equivalent resistance Req of resistors in parallel is:
1Req=n∑i=11Ri
Ohm's Law states that the current (I) flowing through a conductor between two points is directly proportional to the voltage (V) across the two points, provided the temperature remains constant. Mathematically, it can be expressed as:
V=I×R
where R is the resistance of the conductor.
Resistance (R) is defined as the opposition offered by a material to the flow of electric current. It can be calculated using the formula:
R=VI
When resistors are connected in parallel, the voltage across each resistor is the same, but the total current flowing through the circuit is the sum of the currents flowing through each resistor.
Let’s consider n resistors R1,R2,R3,…,Rn connected in parallel. The voltage across each resistor is the same, denoted as V.
- For R1: I1=VR1
- For R2: I2=VR2
- For R3: I3=VR3
- ...
- For Rn: In=VRn
I=I1+I2+I3+…+In
Substituting the expressions for I1,I2,…,In:
I=VR1+VR2+VR3+…+VRn
Factoring V out of the equation:
I=V(1R1+1R2+1R3+…+1Rn)
By Ohm's Law, we can also express the total current in terms of the equivalent resistance Req:
I=VReq
Setting the two expressions for current equal to each other:
VReq=V(1R1+1R2+1R3+…+1Rn)
Dividing both sides by V (assuming V≠0):
1Req=1R1+1R2+1R3+…+1Rn
1Req=n∑i=11Ri
Topper's Solved these Questions
- ELECTRICITYBOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - Based On Practical
10 Videos
- ELECTRICITYBOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - Higher Order Thinking
7 Videos
- ELECTRICITYBOOK - PRADEEPCHAPTER - ELECTRICITYEXERCISE - (Additional)Short Answer
36 Videos
- MAGNETIC EFFECTS OF ELECTRIC CURRENTBOOK - PRADEEPCHAPTER - MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - Mock Test
21 Videos
Similar Questions
Knowledge Check
Equivalent resistance (in ohm) of the given network is
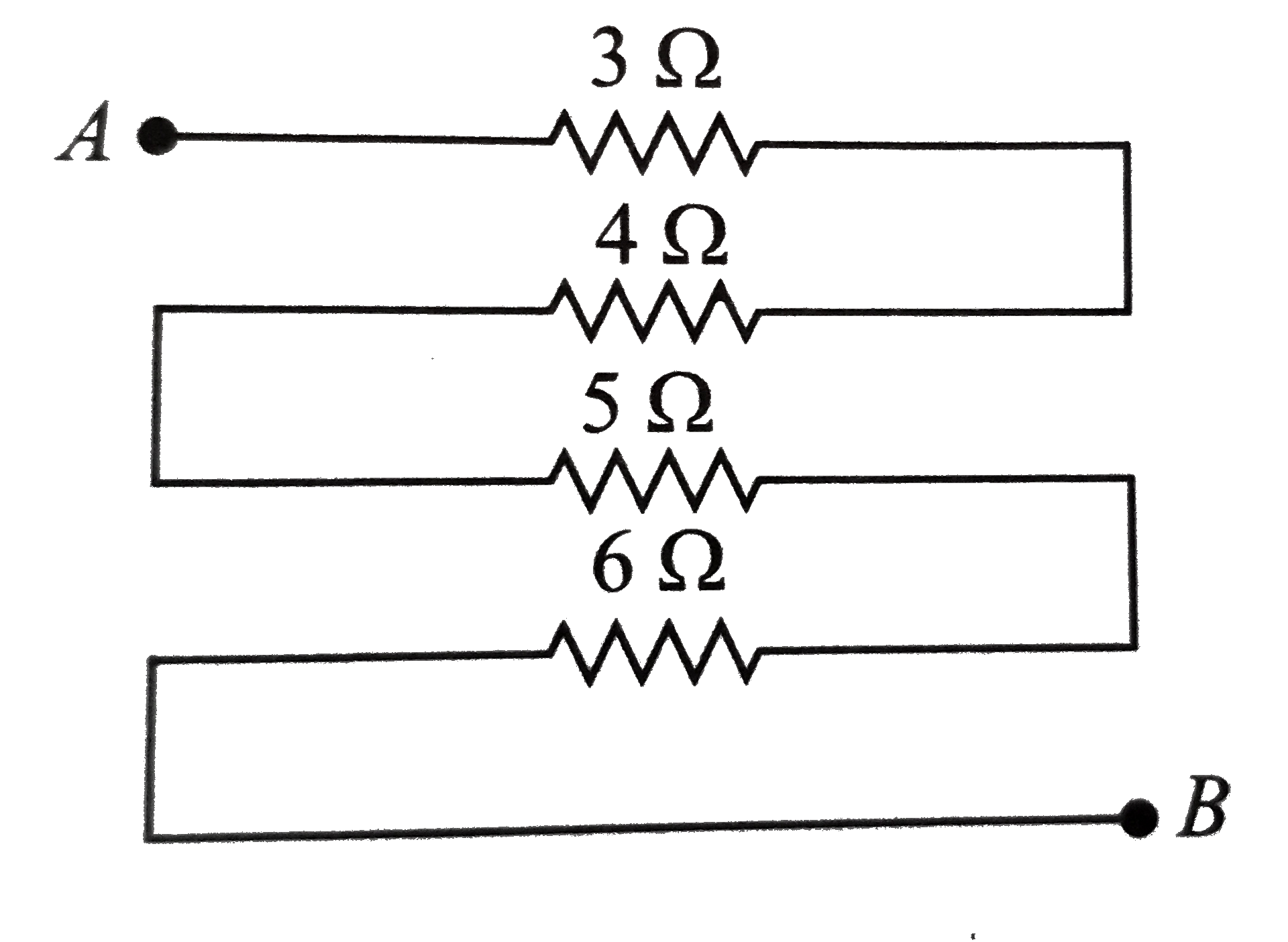 A28B18C26D25
A28B18C26D25Ohm's law expressed as E = IR
Acan never be applied to ACBapplies to AC in the same manner as to DCCalways applies to AC circuits when Z is substituted for RDtells us that Eeff= 0.707 (Emax) for ACThree equal resistances when combined in series are equivalent to 90 ohm. Their equivalent resistance when combined in parallel will be:
A10 ohmB30 ohmC270 ohmD810 ohm
Derive expression for equivalent resistance of a parallel combination of resistances.
(b) Calculate the ratio of equivalent resistance for a series combination of n number of identical resistors to the parallel combination of the same type of n number of resistors.
View SolutionWith the help of a diagram derive the formula for the equivalent resistance of three resistances connected n parallels?
View SolutionState Ohm's law. Derive the laws of resistances, when they are connected: (i) in series (ii) in parallel.
View SolutionWhat is the ratio of equivalent resistance of series combination of n equal resistance to the equivalent resistance in parallel combination of these n resistances ?
View SolutionCalculate the equivalent resistance when two resistances of 3 ohms and 6 ohms are connected in parallel.
View Solution
