With the help of a diagram derive the formula for the equivalent resistance of three resistances connected n parallels?
To derive the formula for the equivalent resistance of three resistances connected in parallel, we can follow these steps:
Step 1: Understand the Parallel Connection
In a parallel connection, the resistances are connected across the same two points, meaning they all experience the same potential difference (voltage) across them. Let's denote the three resistances as \( R_1 \), \( R_2 \), and \( R_3 \).
Step 2: Draw the Circuit Diagram
Draw a circuit diagram showing three resistors connected in parallel. The positive terminal of a battery is connected to one end of all three resistors, and the other ends of the resistors are connected to the negative terminal of the battery.
±−−R1−−−+||||±−−R2−−−+||||±−−R3−−−+∣|∣|±−−−−−−−−−+
Step 3: Apply Kirchhoff’s Current Law
According to Kirchhoff’s Current Law, the total current \( I \) entering a junction is equal to the sum of the currents flowing out of the junction. Thus, we can write:
\( I = I_1 + I_2 + I_3 \)
where \( I_1 \), \( I_2 \), and \( I_3 \) are the currents through resistors \( R_1 \), \( R_2 \), and \( R_3 \) respectively.
Step 4: Relate Current and Voltage
The current through each resistor can be expressed using Ohm's Law, which states \( V = I \cdot R \). Rearranging this gives us:
\( I_1 = \frac{V}{R_1}, \quad I_2 = \frac{V}{R_2}, \quad I_3 = \frac{V}{R_3} \)
where \( V \) is the potential difference across each resistor.
Step 5: Substitute Currents into the Current Equation
Substituting the expressions for \( I_1 \), \( I_2 \), and \( I_3 \) into the current equation gives:
\( I = \frac{V}{R_1} + \frac{V}{R_2} + \frac{V}{R_3} \)
Step 6: Factor Out the Voltage
Since \( V \) is common in all terms, we can factor it out:
\( I = V \left( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \right) \)
Step 7: Relate Total Current to Equivalent Resistance
The equivalent resistance \( R_{\text{eq}} \) of the parallel combination can be defined as:
\( I = \frac{V}{R_{\text{eq}}} \)
Setting the two expressions for \( I \) equal to each other gives:
\( \frac{V}{R_{\text{eq}}} = V \left( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \right) \)
Step 8: Simplify the Equation
Dividing both sides by \( V \) (assuming \( V \neq 0 \)):
\( \frac{1}{R_{\text{eq}}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \)
Step 9: Final Formula
Thus, the formula for the equivalent resistance of three resistors in parallel is:
\( \frac{1}{R_{\text{eq}}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \)
In a parallel connection, the resistances are connected across the same two points, meaning they all experience the same potential difference (voltage) across them. Let's denote the three resistances as \( R_1 \), \( R_2 \), and \( R_3 \).
Draw a circuit diagram showing three resistors connected in parallel. The positive terminal of a battery is connected to one end of all three resistors, and the other ends of the resistors are connected to the negative terminal of the battery.
According to Kirchhoff’s Current Law, the total current \( I \) entering a junction is equal to the sum of the currents flowing out of the junction. Thus, we can write:
\( I = I_1 + I_2 + I_3 \)
where \( I_1 \), \( I_2 \), and \( I_3 \) are the currents through resistors \( R_1 \), \( R_2 \), and \( R_3 \) respectively.
The current through each resistor can be expressed using Ohm's Law, which states \( V = I \cdot R \). Rearranging this gives us:
\( I_1 = \frac{V}{R_1}, \quad I_2 = \frac{V}{R_2}, \quad I_3 = \frac{V}{R_3} \)
where \( V \) is the potential difference across each resistor.
Substituting the expressions for \( I_1 \), \( I_2 \), and \( I_3 \) into the current equation gives:
\( I = \frac{V}{R_1} + \frac{V}{R_2} + \frac{V}{R_3} \)
Since \( V \) is common in all terms, we can factor it out:
\( I = V \left( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \right) \)
The equivalent resistance \( R_{\text{eq}} \) of the parallel combination can be defined as:
\( I = \frac{V}{R_{\text{eq}}} \)
Setting the two expressions for \( I \) equal to each other gives:
\( \frac{V}{R_{\text{eq}}} = V \left( \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \right) \)
Dividing both sides by \( V \) (assuming \( V \neq 0 \)):
\( \frac{1}{R_{\text{eq}}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \)
Thus, the formula for the equivalent resistance of three resistors in parallel is:
\( \frac{1}{R_{\text{eq}}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \)
Topper's Solved these Questions
Similar Questions
(a) With the help of a diagram, derive the formula for the resultant resistance of these resistors connected in series.
(b) For the circuit shown in the diagram given below:
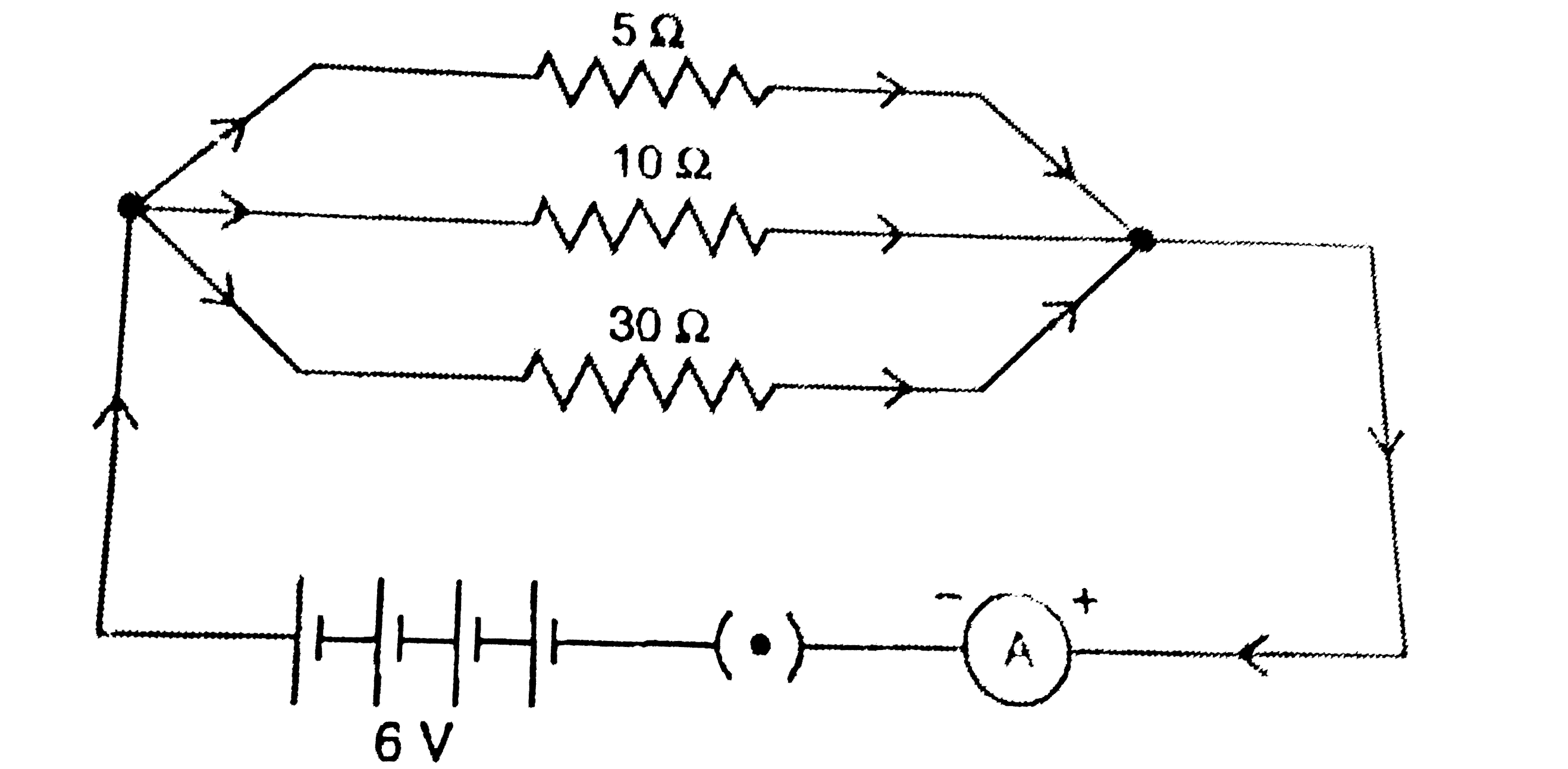
Calculate:
(i) the value of current each resistor.
(ii) the total current in the circuit.
(iii) the total effective resistance of the circuit.
View Solution(a) With the help of a circuit diagram, obtain the relation for the equivalent resistance of two resistances connected in parallel.
(b) In the circuit diagram shown below, find:
(i) Total resistance.
(ii) Current shown by the ammeter A
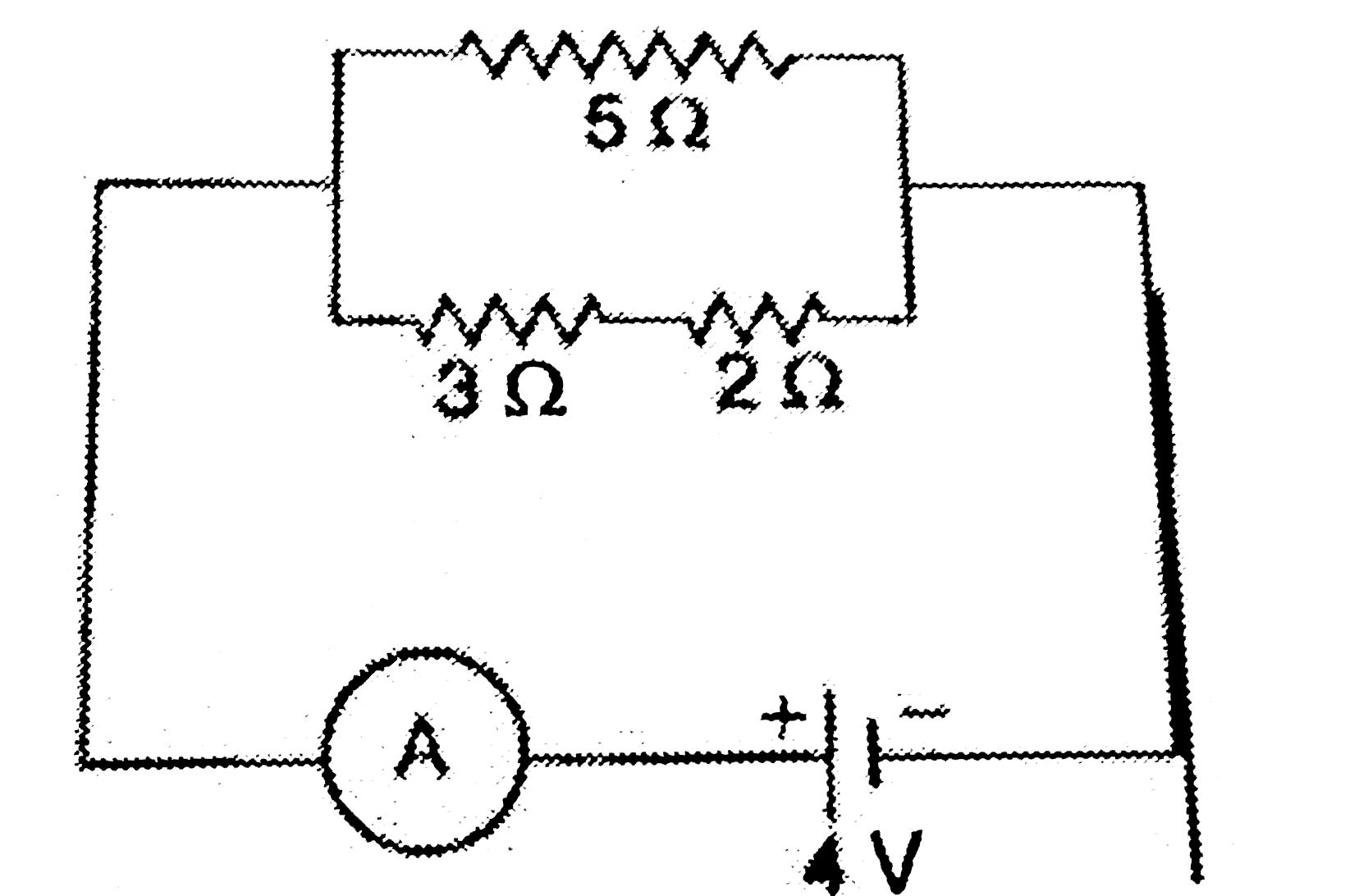
View Solution
Knowledge Check
The effective resistance of three equal resistances, each of resistance r, connected in parallel, is
A3/rBr/3C3rDr3The reciprocal of the combined resistance of any number of resistance connected in parallel is equal to
Athe sum of reciprocals of individual resistancesBreciprocal of the product of individual resistancesCreciprocal of sum of all the resistancesDNone of the above
(a) With the help of a circuit diagram, deduce the equivalent resistance of two resistances connected in series.
(b) Two resistances are connected in series as shown in the diagram:
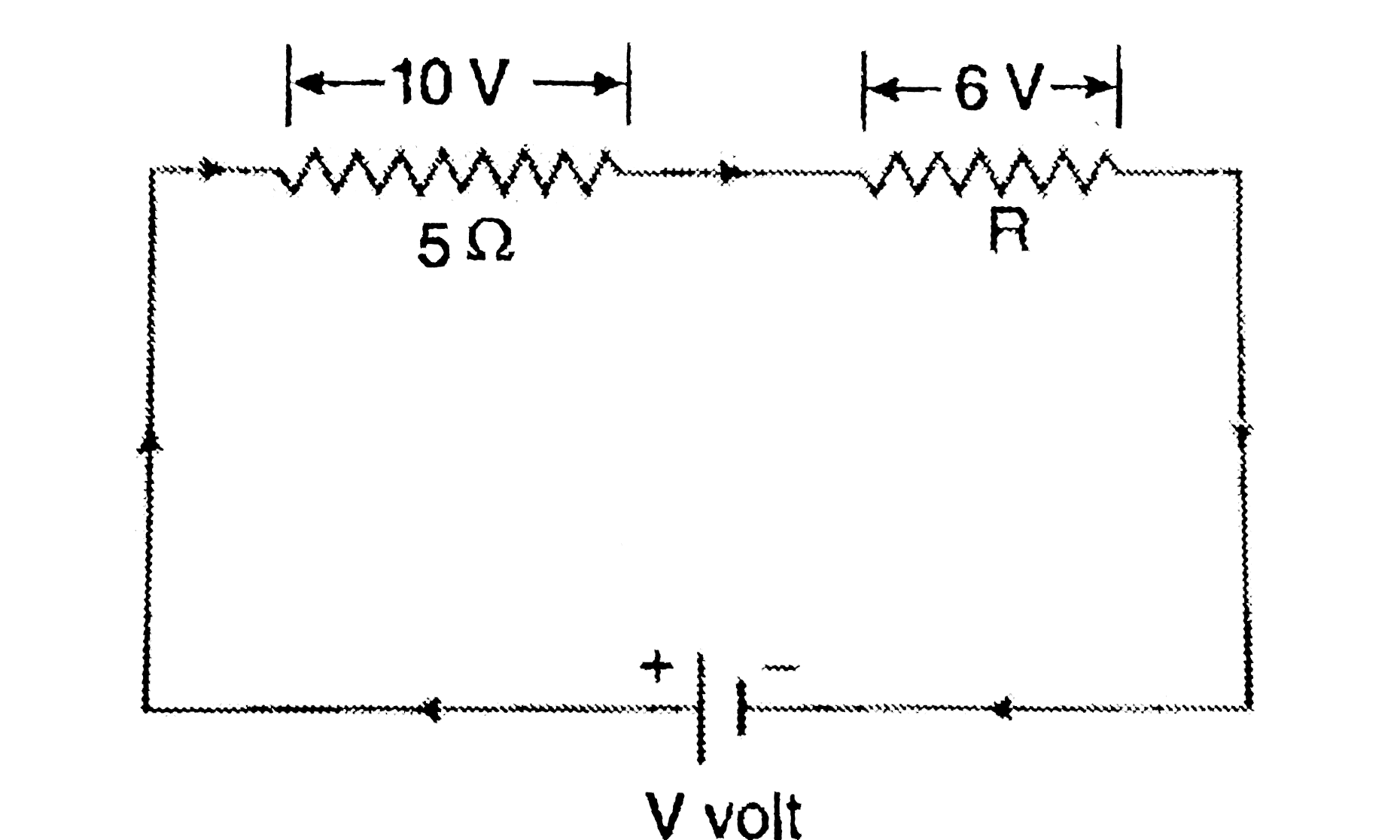
(i) What is the current through the 5 ohm resistance?
(ii) What is the current through R?
(iii) What is the value of R?
(iv) What is the value of V?
View SolutionFind an expression for equivalent resistance of three resistors joined in parallel.
View Solution(a) With the help of a suitable circuit diagram peove that the reciprocal of the equivalent
resistance of a group of resistances joined in parallel is equal to the sym of the
reciprocals of the individual resistances.
(b) In an electric circuit two resistors of 12Ω each are joined in parallel to a 6V battery.
Find the current drawn from the battery.
View SolutionThree resistances of 2Ω,3Ωand6Ω are first connected in series and the equivalent resistance is found to be……… Then the three resistances are connected in parallel Now its equivalent resistance is………
View SolutionState Ohm's law. Derive an expression for the equivalent resistance of a number of resistances in parallel.
View SolutionCalculate the equivalent resistance when two resistances of 3 ohms and 6 ohms are connected in parallel.
View Solution