State one way to reduce the moment of a given force about a given axis of rotation.
To solve the question, "State one way to reduce the moment of a given force about a given axis of rotation," we can follow these steps:
1. Understand the Concept of Moment of Force:
The moment of a force (also known as torque) about an axis of rotation is defined as the product of the force and the perpendicular distance from the axis of rotation to the line of action of the force. The formula is given by:
Moment of Force=Force×Perpendicular Distance
2. Identify Ways to Reduce the Moment:
To reduce the moment of a force, we can either:
- Decrease the magnitude of the force applied.
- Decrease the perpendicular distance from the axis of rotation to the line of action of the force.
3. State One Method:
For the purpose of this question, we can choose one method. For example, we can state:
"One way to reduce the moment of a given force about a given axis of rotation is to decrease the perpendicular distance from the axis of rotation to the line of action of the force."
Final Answer:
One way to reduce the moment of a given force about a given axis of rotation is to decrease the perpendicular distance from the axis of rotation to the line of action of the force.
---
The moment of a force (also known as torque) about an axis of rotation is defined as the product of the force and the perpendicular distance from the axis of rotation to the line of action of the force. The formula is given by:
Moment of Force=Force×Perpendicular Distance
To reduce the moment of a force, we can either:
- Decrease the magnitude of the force applied.
- Decrease the perpendicular distance from the axis of rotation to the line of action of the force.
For the purpose of this question, we can choose one method. For example, we can state:
"One way to reduce the moment of a given force about a given axis of rotation is to decrease the perpendicular distance from the axis of rotation to the line of action of the force."
One way to reduce the moment of a given force about a given axis of rotation is to decrease the perpendicular distance from the axis of rotation to the line of action of the force.
Topper's Solved these Questions
- FORCE BOOK - ICSECHAPTER - FORCE EXERCISE - EXERCISE 1(A) Multiple choice questions
2 Videos
- FORCE BOOK - ICSECHAPTER - FORCE EXERCISE - EXERCISE 1(A) Numericals
18 Videos
- FORCE BOOK - ICSECHAPTER - FORCE EXERCISE - EXERCISE 1( C) Multiple Choice questions
2 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS
1 Videos
- HOUSEHOLD CIRCUITS BOOK - ICSECHAPTER - HOUSEHOLD CIRCUITS EXERCISE - EXERCISE -9(B) (MULTIPLE CHOICE TYPE)
2 Videos
Similar Questions
Knowledge Check
The moment of a force about a given axis depends:
A(a) only on the magnitude of forceB(b) only on the perpendicular distance of force from the axisC(c) neither on the force nor or the perpendicular distance of force from the axisD(d) both, on the force and its perpendicular distance from the axis.One quarter sector is cut from a uniform circular disc of radius R. The sector has mass M. IT is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. Its moment of inertia about the axis of rotation is
AMR2/2BMR2/4CMR2/8D√2MR2
The moment of inertia of a body about a given axis of rotation depends upon :-
View SolutionCalculate the moment of inertia of the given rod about an axis CD
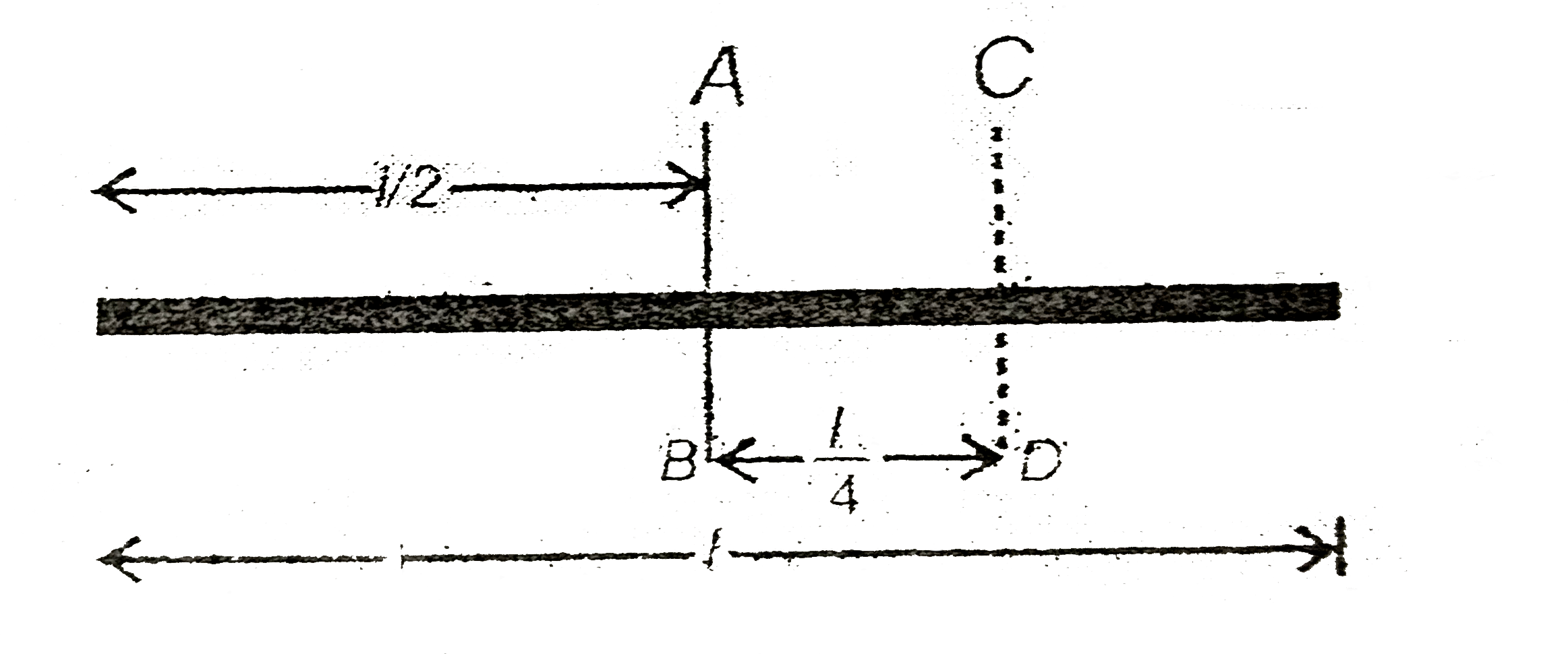
View SolutionCalculate the moment of inertia of the given rod about an axis CD.
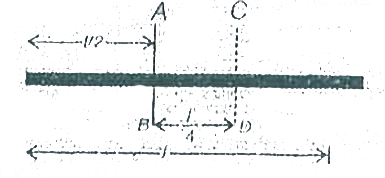
View SolutionOne quarter sector is cut from a uniform circular disc of radius R. This sector has mass M. It is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. It moment of inertia about the axis of rotation is.
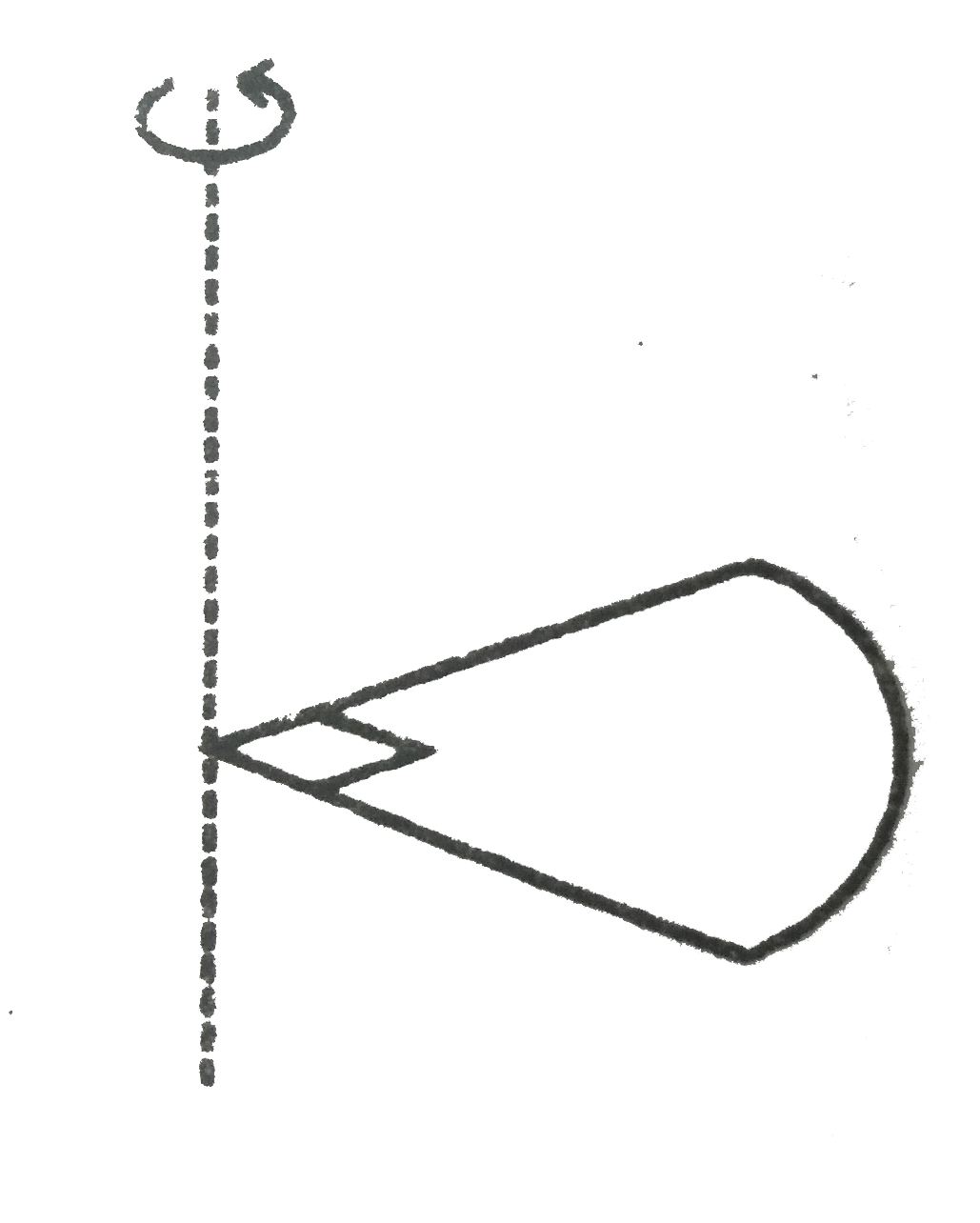 .
.
View SolutionA particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10ms2)
View SolutionA rigid body is rotating about a vertical axis. In t second, the axis gradually becomes horizontal. But the rigid body continues to make v rotations per second throughout the time interval of 1 second. If the moment of inertia I of the body about the axis of rotation can he taken as constant, then the torque acting on the body is
View Solution
