State the law which relates to the generation of induced emf in a conductor being moved in a magnetic field.
Apply this law to obtain an expression for the induced emf when one .rod. of a rectangular conductor is free to move in a uniform, time independent and .normal. manetic field.
Apply the concept of the Lorentz (magnetic) force acting on a moving charge to justify the expression obtained.

Text Solution

Verified by Experts

Farday.s law of electromagnetic induction : It states that the induced emf is equal to the rate of change of magnetic flux.
That $E = - \frac{d ϕ}{d t}$ ...(i)
But $E = \to \oint \to E \cdot \to d l$ and $ϕ = \oint_{S} \to B \cdot - \to d S$ ...(ii)
Hence the above relation may be written as
$\oint \to E \cdot \to d l = \oint_{S} \frac{d \to B}{d t} d \to S$ ...(iii)
Induced emf by Changing the Area A. Suppose a uniform magnetic field B perpendicular to the plane of the paper and directed outwards [shown by dots in Fig.] is confined in region PQRS. Let a rectangular loop of wire KLMN be held partially in the magnetic field in the plane of the paper. Let $K L = l$ . Suppose $x$ is the portion of the loop in the field at any instant. t. When the loop is moved with a velocity $v$ in the plane of the paper, area of the loop associated with the magnetic field changes. An induced emf is set up in the wire. This is detected by deflection in the galvanometer G connected in the loop.

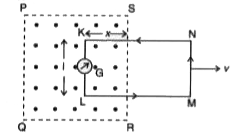
To calculate the emf induced, suppose in a small time $Δ t$ , the loop is moved out of magnetic field through a small distance $Δ x$ .
$∴$ Decrease in area of the loop
$= - l Δ x$
Decrease in magnetic flux linked with the loop
$d ϕ = - B l Δ x$
As induced emf,
$ε = - d ϕ / d t$
$∴ ε = \frac{B l Δ x}{Δ t} = B l v$
i.e., $ε = B l v$
It is also possible to explain the motional emf expression by invorking the Lorentz force acting on the free charge carriers of conductor PQ. Consider any arbitrary charge q in the conductor PQ. When the rod moves with a speed v, the charge will also be moving with speed v in the magnetic magnitude, and its direction is towards Q. All charges experience the same force, in magnitude and direction, irrespective of their position in the rod PQ. The work done in moving the charge from P to Q is.
$W = q v B l$
Since emf is the work done per unit charge.
$ε = \frac{W}{q}$
$= B l v$
This equation gives emf induced across the rod PQ.

If a straight conductor is moved with a uniform velocity at right angle to a uniform magneti field then e.m.f. induced in it is
A $e = - B / v$
B $e = B / v^{2}$
C $e = B / l v$
D $e = l / v B$
If a conductor is rotating about its one end in a uniform magnetic field then an emf induced in it is
A $e = - B A f$
B $e = + B A f^{2}$
C $e = B / A f$
D $e = B$
A moving conductor coil in a magnetic field produces an induced e.m.f. This is in accordance with
AAmperes law
BCoulomb law
CLenz’s law
DFaraday’s law