State the parallelogram law of vectors and derive an expression for its magnitude

Text Solution

Verified by Experts

Parallelogram Law : If two vectors can be represented by the two adjacent sides of a parallelogram then the diagonal passing through the intersection of given vectors represents their resultant both in direction and magnitude
Proof : Let $¯ ¯ ¯ P and ¯ ¯ ¯ Q$ are two adjacent vectors with an angle $. θ .$ between them . Construct a parallelogram OACB with OA $= ¯ ¯ ¯ P and O B = ¯ ¯ ¯ Q$ as adjacent sides . Extend the line OA and drop an normal D from C . The diagonal OC gives the resultant $¯ ¯ ¯ R$ both in direction and magnitude

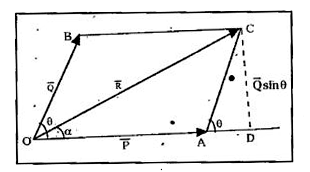
in figure OCD is a right angle triangle
$∴ O C^{2} = O D^{2} + D C^{2}$
But $O D = O A + A D = ¯ ¯ ¯ P + ¯ ¯ ¯ Q cos θ$
and $C D = ¯ ¯ ¯ Q sin θ and O C = ¯ ¯ ¯ R$
$∴ {¯ ¯ ¯ R}^{2} = {[¯ ¯ ¯ R + ¯ ¯ ¯ Q cos θ]}^{2} + {[¯ ¯ ¯ Q sin θ]}^{2}$
${¯ ¯ ¯ R}^{2} = {¯ ¯ ¯ P}^{2} + {¯ ¯ ¯ Q}^{2} {cos}^{2} θ + 2 ¯ ¯¯¯¯ ¯ P Q cos θ + {¯ ¯ ¯ Q}^{2} {sin}^{2} θ$
$∴ {¯ ¯ ¯ R}^{\circ} = {¯ ¯ ¯ P}^{2} + {¯ ¯ ¯ Q}^{2} ({sin}^{2} θ + {cos}^{2} θ) + 2 ¯ ¯¯¯¯ ¯ P Q cos θ$
But ${sin}^{2} θ + {cos}^{2} θ = 1$
$∴ {¯ ¯ ¯ R}^{2} = {¯ ¯ ¯ P}^{2} + {¯ ¯ ¯ Q}^{2} + 2 ¯ ¯¯¯¯ ¯ P Q cos θ$
Resultant vector $, ¯ ¯ ¯ R = \sqrt{{¯ ¯ ¯ P}^{2} + {¯ ¯ ¯ Q}^{2} + 2 ¯ ¯¯¯¯ ¯ P Q cos θ}$
Angle of resultant with adjacent side $. α .$
$tan α = \frac{C D}{O D} (∴ O D = O A + A D)$
Tan $α \frac{C D}{O A + a D} = \frac{¯ ¯ ¯ Q sin θ}{¯ ¯ ¯ P + ¯ ¯ ¯ Q cos θ}$ ( $∴ A D = ¯ ¯ ¯ Q cos θ$ )
Angle of $¯ ¯ ¯ R$ with adjacent side, $α = {tan}^{- 1} [\frac{¯ ¯ ¯ Q sin θ}{¯ ¯ ¯ P + ¯ ¯ ¯ Q cos θ}]$

Updated on:21/07/2023

In parallelogram law of vector, the direction of resultant vector is given by
A $tan α = \frac{Q cos θ}{P + Q sin θ}$
B $tan α = \frac{Q sin θ}{P + Q cos θ}$
C $tan α = \frac{P sin θ}{P + Q cos θ}$
D $tan α = \frac{P cos θ}{P + Q cos θ}$
Parallelogram law of vectors is applicable to the addition of $:$
AAny two vectors
BTwo scalars
CA vector and a scallar
DTwo vectors representing same physical quantity.