obtain an expression for the acceleration of a body down a rough inclined plane

Text Solution

Verified by Experts

Let a body of mass m is place on a rough incline. Let the angle of inclination $. θ .$ is gradually increased for a particular angle $θ = α$ called angle of repose the body will side down the inclined plane with acceleration
When $θ > α$ the body will slide down the rough incline with some resultant acceleration
The focus acting on the body m are

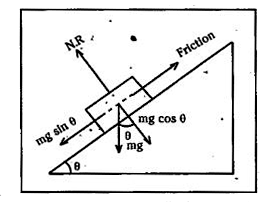
1) Weight of the body W =mg vertically downwards by resolving weight W = mg
a) component mg $\cos θ$ will balance N.R.
b) Component mg $\sin θ$ will be useful for downward motion
c) Force of friction $F = μ m g \cos θ$
Downward acceleration a $= \frac{Resultant force F_{R}}{mass m}$
Resultant force on the body $= m g \sin θ$ - Friction $(μ m g \cos θ)$
$∴$ Downward acceleration, a $\frac{m g \sin θ - μ m g \cos θ}{m}$
$∴ a = g (\sin θ - μ \cos θ)$

|

Updated on:21/07/2023

Class 11 PHYSICS MODEL PAPER 11

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The acceleration of a moving body down a rough inclined plane is
A $g (sin θ + μ cos θ)$
B $g (sin θ - μ cos θ)$
C $g sin θ$
D $g cos θ$
Question 2 - Select One
Assertion: The acceleration of a body down a rough inclined plane is grater than the acceleration due to gravity.
Reason: The body is able to slide on an inclined plane only when its acceleration is greater than acceleration due to gravity.
AIf both assertion and reason are true and reason is the correct explanation of assertion.
BIf both assertion and reason are true but reason is not the correct explanation of assertion
CIf assertion is true but reason is false.
DIf both aseertion and reason are false.
Question 3 - Select One
A solid sphere slides down a smooth inclined plane of inclination $θ$ with acceleration $a_{1}$ . A disc rolls down a rough inclined plane of inclination $θ$ with acceleration $a_{2}$ . Value of $\frac{a_{1}}{a_{2}}$ is
A $\frac{3}{2}$
B $\frac{2}{3}$
C $\frac{1}{2}$
D2

VGS PUBLICATION-BRILLIANT-MODEL PAPER 11-Section - B

Home
Ask Doubt
Profile