Suppose in an insulating medium, having di-electric constant k= 1, volume density of positive charge varies with y-coordinate according to law ρ=ay. A particle of mass m having positive charge q is placed in the medium at point A (0,y0)J and projected with velocity →v=v0ˆi as shown in figure. Neglecting gravity and frictional resistance of the medium and assuming electric field strength to be zero at y = 0, calculate slope of trajectory of the particle as a function of y :

The correct Answer is:⎡⎢⎣√qa3mε0v20(y3−y30)⎤⎥⎦
Step by step video, text & image solution for Suppose in an insulating medium, having di-electric constant k= 1, volume density of positive charge varies with y-coordinate according to law rho = ay. A particle of mass m having positive charge q is placed in the medium at point A (0,y_(0))J and projected with velocity vecv = v_(0)hati as shown in figure. Neglecting gravity and frictional resistance of the medium and assuming electric field strength to be zero at y = 0, calculate slope of trajectory of the particle as a function of y : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Advance MCQs
40 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Advance MCQs
33 Videos
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems
107 Videos
Similar Questions
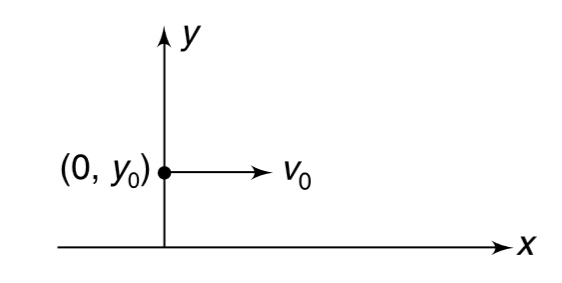
Electric field in xy plane is directed along positive y direction and its magnitude changes with y co-ordinate as E=ay2
A particle having charge q and mass m is projected at point (0,y0) with velocity
→v=v0ˆi
Neglect all other forces o the particle apart from the electric force. Calculate the slope of the trajectory of the particle as a function of y.
View SolutionIn an insulating medium (dielectric constant =1) the charge density varies with y Co-ordinate as ρ=by, where b is a positive constant.t he electric field is zero at y=0 and everywhere else it is along y direction. Calculate the electric field as a function of y.
View Solution
Knowledge Check
A particle of mass m and charge q is thrown in the vertical direction with a velocity v0 in a uniform horizontal electric field E. Assuming the gravity force to be negligible ,the equation of the path followed by the particle will be
Aparabola ,x=(qE2mv20)y2Bhyperbola , x=qE2mv20yCstraight line ,x=qEy2mv20Dnone of the aboveA particle of mass m and having a positive charge q is projected from origin with speed v0 along the positive X-axis in a magnetic field B = −B0ˆK, where B0 is a positive constant. If the particle passes through (0,y,0), then y is equal to
A−2mv0qB0Bmv0qBC−mv0qBD2mv0qB0Electric field strength →E=E0ˆi and →B=B0ˆi exists in a region. A charge is projected with a velocity →v=v0ˆj origin, then
AIt moves along helix with constant pitchBIt moves along circular path in Y Z planeCIt moves along helix with increasing pitchDIt moves along helix with decreasing pitch
A charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionA positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
View SolutionA charge particle of charge q, mass m is projected with a velocity →v=vˆi in a region of space where electric field strength →E=Eˆk and magnetic induction →B=Bˆj are present. The acceleration of the particle is:
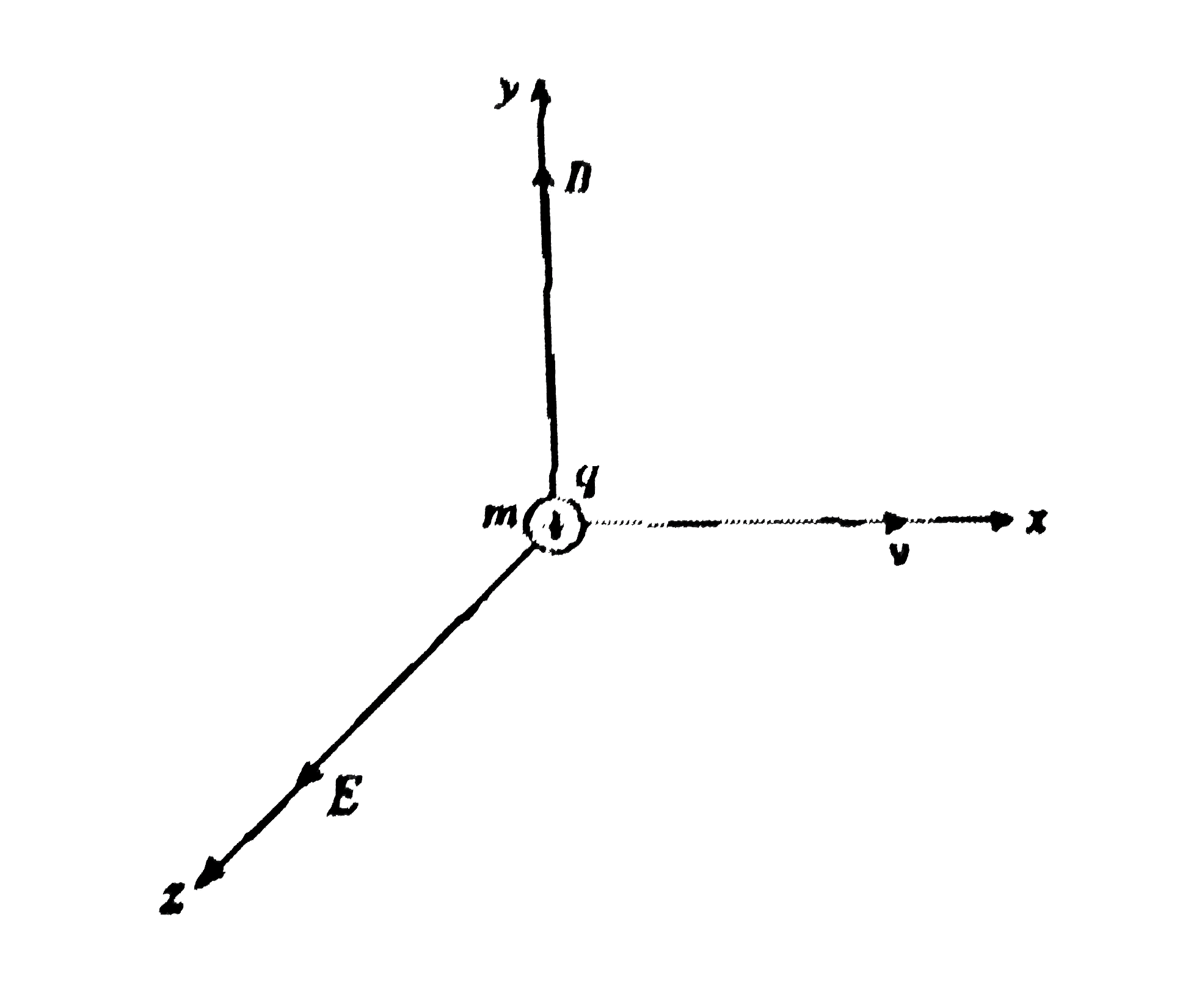
View SolutionCharge 2qand−q are placed at (a,0)and(−a,0) as shown in the figure. The coordinates of the point at which electric field intensity is zero will be (x,0) where

View SolutionA particle of mass m and positive charge q is projected with a speed of v0 in y–direction in the presence of electric and magnetic field are in x–direction. Find the instant of time at which the speed of particle becomes double the initial speed.
View Solution
