Suppose the initial charge on the capactor in the above question is 6 mC. What is the total energy stored in the capactor intially ? What is the total energy at later time ?
Text Solution
Capacitance of the capacitor, C=30μF=30×10−6F
Inductance of the inductor, L=27mH=27×10−3H
Charge on the capacitor, Q=6mC=6×10−3C
Total energy stored in the capacitor can be calculated by the relation
E=12Q2C
=12×(6×10−3)230×10−6
=610=0.6J
Total energy at a later time will remain the same because energy is shared between the capacitor and the inductor.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Find out total energy stored in the capacitors.
A500μJB300μJC600μJD1300μJ
Find the total energy stored in the capacitors in the given network.
 View Solution
View SolutionIn what form is the energy stored in a charged capacitance ?
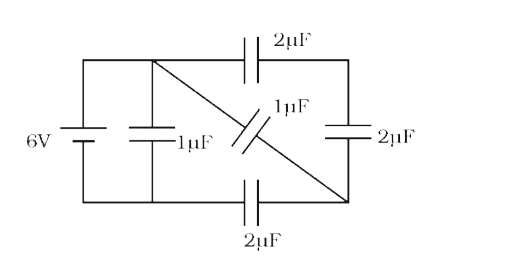
View SolutionFind total energy stored in capacitors given in the circuit.
 View Solution
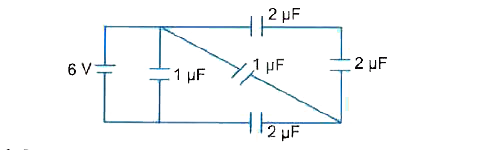
View SolutionFind total energy stored in capacitors given in the circuit
 View Solution
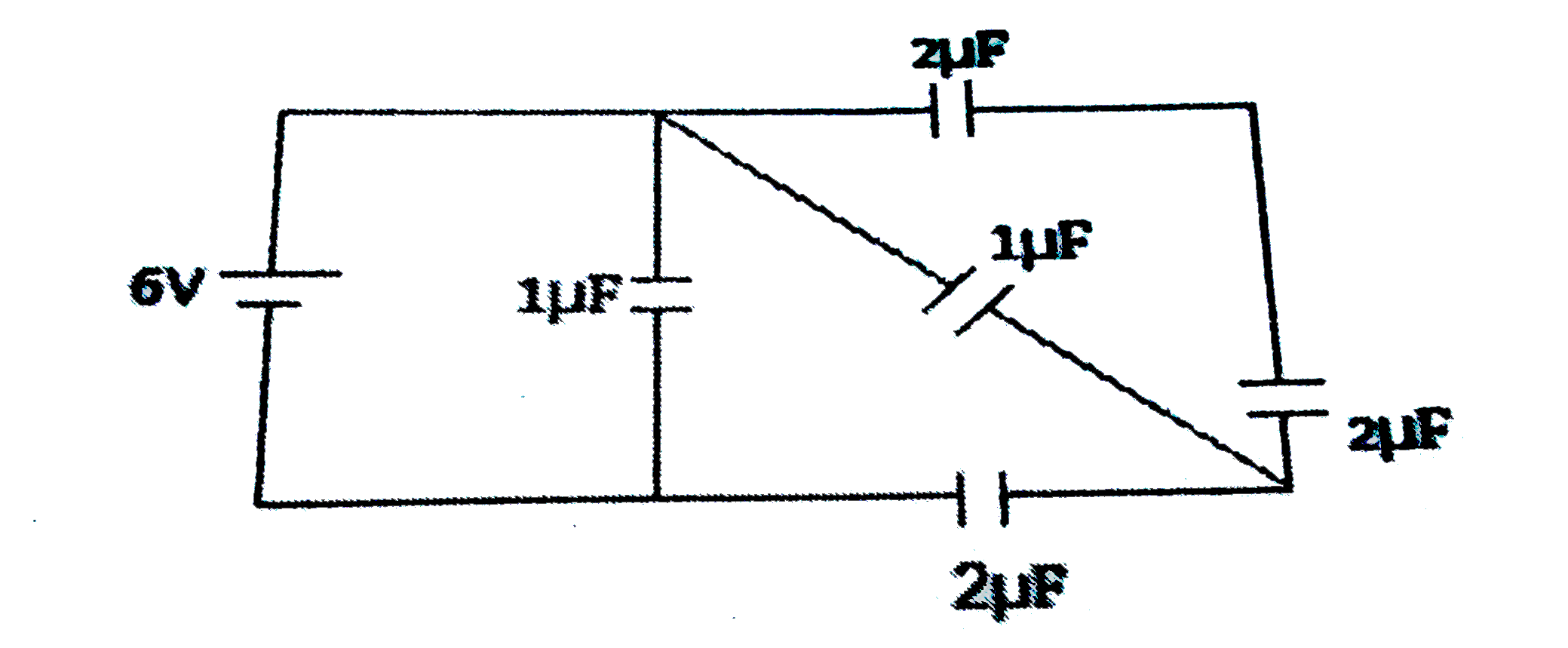
View SolutionFind total energy stored in capacitors given in the circuit
 View Solution
View SolutionTwo men, B and C run around a circular track of length 500m in opposite directions with initial speeds of 4m/s and 1m/s respectively starting from the same point simultaneously. Whenever they meet, B’s speed halfs and C’s speed doubles, after how much time will they meet for the 3rd time?
View SolutionThe total electrostatic energy stored in both the capacitor is
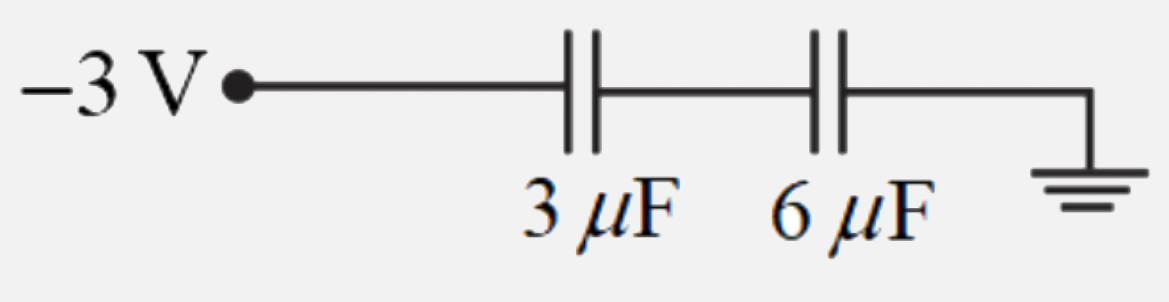 View Solution
View Solution

