The accleration of a particle as seen from two frames S1 and S2 have equal magnitudes 4 m/s2
the frames must be at rest with respect to each other
the frames may be moving with respect to each other but neither should be acclerated with respect to the other
the accleration of S2 with respect of S1 may be either zero or 8 m/s2.
the acceleration of S2 with respect to S1 may have any value between zero and 8m/s2
The correct Answer is:d
To solve the problem, we need to analyze the relationship between the accelerations of the two frames of reference, S1 and S2, as well as the particle's acceleration in these frames.
1. Understanding the Given Information:
- The acceleration of a particle as seen from frame S1 is ap/S1=4m/s2.
- The acceleration of the same particle as seen from frame S2 is ap/S2=4m/s2.
2. Using the Relative Acceleration Formula:
- The relative acceleration of frame S2 with respect to frame S1 can be expressed as:
aS2/S1=ap/S1+aS1/p
- Here, aS1/p is the acceleration of frame S1 with respect to the particle.
3. Calculating the Relative Acceleration:
- Since both frames observe the particle with the same acceleration of 4m/s2, we can denote:
aS1/p=4m/s2
- Therefore, we can write:
aS2/S1=ap/S1+ap/S2=4+4=8m/s2
4. Considering the Angle Between Accelerations:
- The actual relative acceleration can vary depending on the angle θ between the two acceleration vectors. The formula for the resultant acceleration is:
aS2/S1=√a2p/S1+a2p/S2+2⋅ap/S1⋅ap/S2⋅cos(θ)
- Plugging in the values:
aS2/S1=√42+42+2⋅4⋅4⋅cos(θ)
=√16+16+32⋅cos(θ)
=√32+32⋅cos(θ)
5. Finding the Range of the Resultant Acceleration:
- The value of cos(θ) can vary from -1 to 1:
- If cos(θ)=1 (when the accelerations are in the same direction):
aS2/S1=√32+32=√64=8m/s2
- If cos(θ)=−1 (when the accelerations are in opposite directions):
aS2/S1=√32−32=√0=0m/s2
6. Conclusion:
- Therefore, the acceleration of S2 with respect to S1 can take any value between 0m/s2 and 8m/s2.
Final Answer:
The correct option is:
D: The acceleration of S2 with respect to S1 may have any value between 0 and 8m/s2.
- The acceleration of a particle as seen from frame S1 is ap/S1=4m/s2.
- The acceleration of the same particle as seen from frame S2 is ap/S2=4m/s2.
- The relative acceleration of frame S2 with respect to frame S1 can be expressed as:
aS2/S1=ap/S1+aS1/p
- Here, aS1/p is the acceleration of frame S1 with respect to the particle.
- Since both frames observe the particle with the same acceleration of 4m/s2, we can denote:
aS1/p=4m/s2
- Therefore, we can write:
aS2/S1=ap/S1+ap/S2=4+4=8m/s2
- The actual relative acceleration can vary depending on the angle θ between the two acceleration vectors. The formula for the resultant acceleration is:
aS2/S1=√a2p/S1+a2p/S2+2⋅ap/S1⋅ap/S2⋅cos(θ)
- Plugging in the values:
aS2/S1=√42+42+2⋅4⋅4⋅cos(θ)
=√16+16+32⋅cos(θ)
=√32+32⋅cos(θ)
- The value of cos(θ) can vary from -1 to 1:
- If cos(θ)=1 (when the accelerations are in the same direction):
aS2/S1=√32+32=√64=8m/s2
- If cos(θ)=−1 (when the accelerations are in opposite directions):
aS2/S1=√32−32=√0=0m/s2
- Therefore, the acceleration of S2 with respect to S1 can take any value between 0m/s2 and 8m/s2.
The correct option is:
D: The acceleration of S2 with respect to S1 may have any value between 0 and 8m/s2.
Similar Questions
Acceleration of a particle as seen from two reference frames 1 and 2 has magnitude 3m/s2 and 4m/s2 respectively. What can be magnitude of acceleration of frame 2 with respect to frame 1?
View SolutionA particle is found to be at rest when seen from a frame S1 and moving with a constant velocity when seen from another frame S2. Select the possible options :
View Solution
Knowledge Check
The magnitude of acceleration of a particle as seen by observer A is a m/s2and that observed by Bis b m/s2. If magnitude of acceleration of A with respect to B is x m/s2 then indicate the correct statements is :
A∣∣a2−b2∣∣≤x≤∣∣a2+b2∣∣B|a−b|≤x≤|a+b|C|a−b|<x<|a+b|D0≤x≤|a−b|orx≥|a+b|Statement I: A particle is found to be a rest when seen from a frame S1 and moving with a constant velocity when seen from another frame S2. We can say both the frames are inertial.
Statement II: All frames moving uniformly with respect to an inertial frame are themselves inertial.AStatement I is true, statement II is true, Statement II is the correct explanation for statement I.BStatemet I is true, Statement II is true , Statement II is NOT the correct explanation for Statement ICStatement I is True, Statement II is False.DStatement I is False, Statement II is trueIn S.H.M., the velocity of the particle at the mean position is 1 m/s and acceleration at the extremity is 2m/s2, the period of motion is
A2 sB0.5 sC1 sD3.142 s
Two sources S1 and S2 separated 2.0 m, vibrate according to equation y1=0.03sinπt and y2=0.02sinπt where y1,y2 and t are in M.K.S unit. They send out waves of velocity 1.5 m/s. Calculate the amplitude of the resultant motion of the particle co-linear with S1 and S2 and located at a point to the left of S1.
View SolutionA constatnt force of 10 N act on a block as shown in figure intal velocity of the particle is zero. It is observed from three frames of reference S1,S2 and ground. The frame S1 start from rest and move with constnat acceleration 10m/s. The frames S1andS2 and particle start moving simultaneously at t=0.
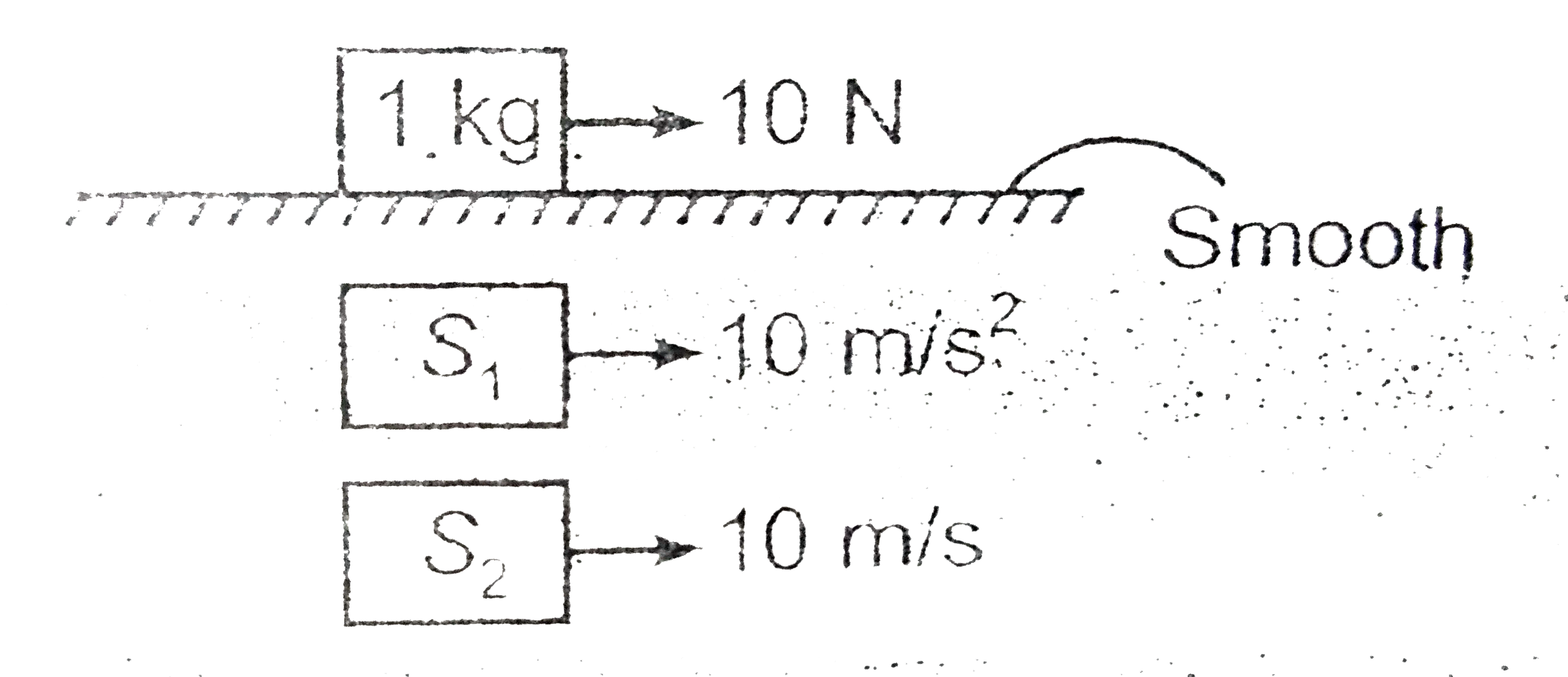
Net work done on block in 1 s as observed from frame S2 is
View SolutionA constatnt force of 10 N act on a block as shown in figure intal velocity of the particle is zero. It is observed from three frames of reference S1,S2 and ground. The frame S1 start from rest and move with constnat acceleration 10m/s. The frames S1andS2 and particle start moving simultaneously at t=0.
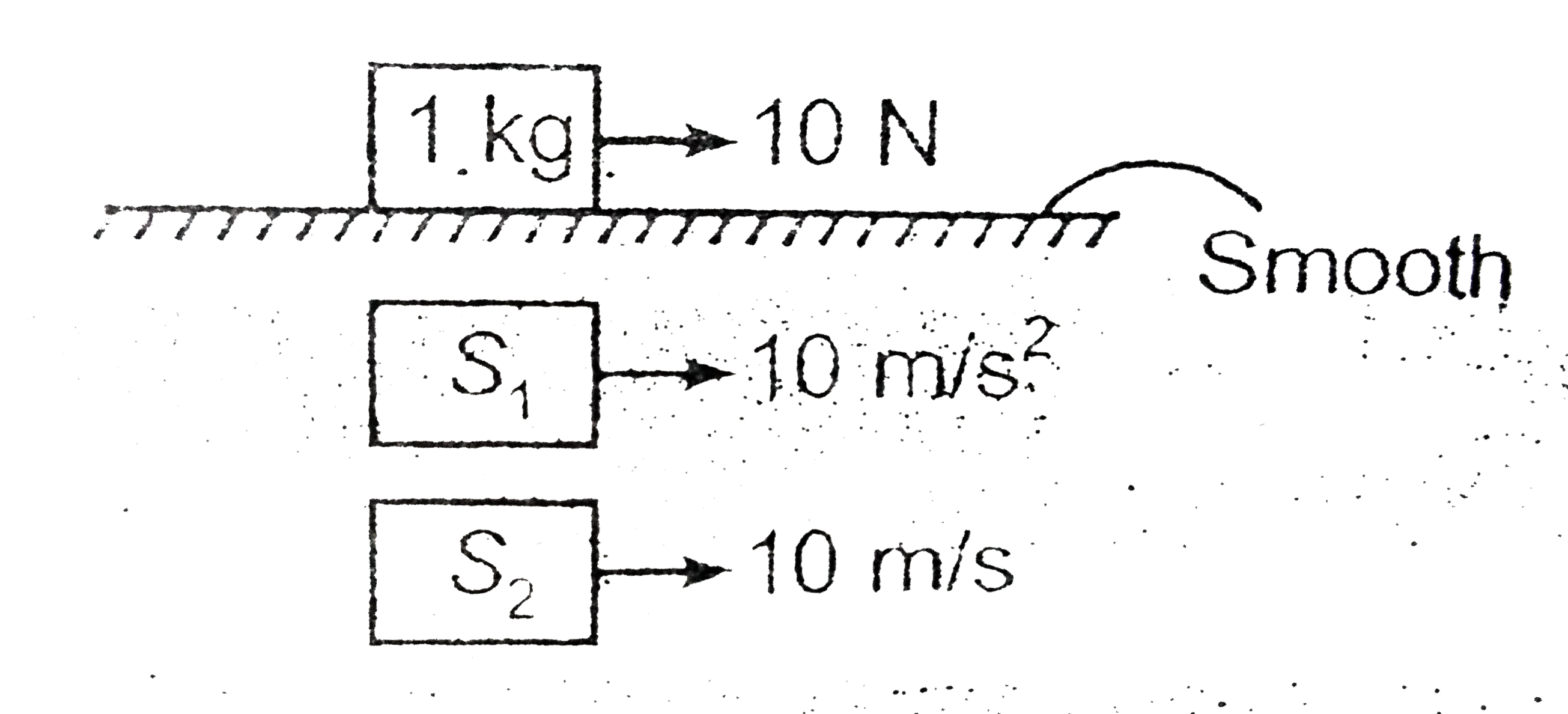
Work done on block in 1 s as observed from frame S1 is
View SolutionA constatnt force of 10 N act on a block as shown in figure intal velocity of the particle is zero. It is observed from three frames of reference S1,S2 and ground. The frame S1 start from rest and move with constnat acceleration 10m/s. The frames S1andS2 and particle start moving simultaneously at t=0.
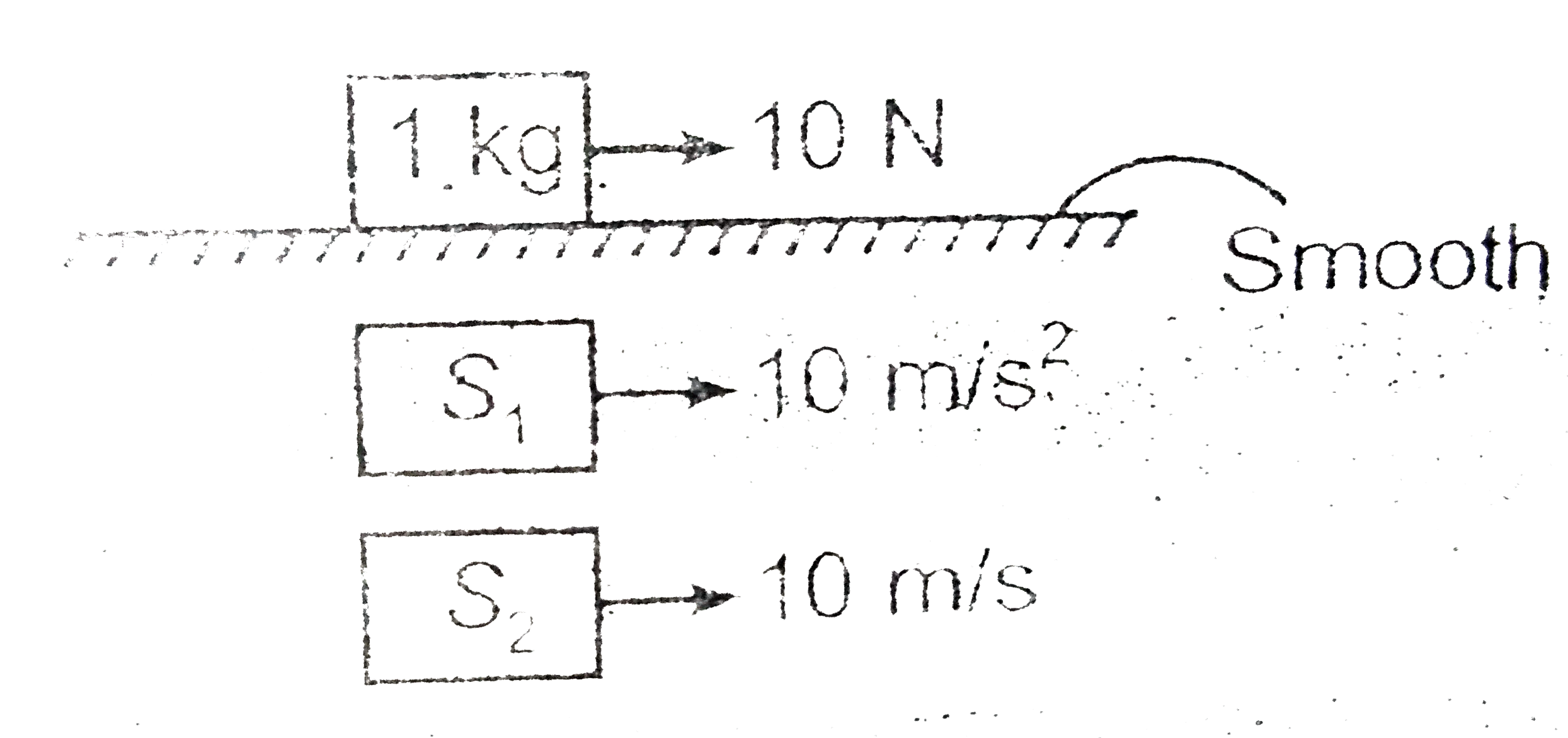
The rate at which work is done by constant force on the particle is always non-negative when observed fom
View SolutionA particle is observed from two frames S1andS2. The frame S2 moves with respect to S1 with an acceleration a. Let F1andF2 be the pseudo forces on the particle when seen from S1andS2 respectively. Which of the following are not possible ?
View Solution
