The angle between two vector A and B is $θ$ . Vector R is the resultant of the two vectors. If R makes an angle $\frac{θ}{2}$ with A, then

A

$A = 2 B$

B

$A = B / 2$

C

$A = B$

D

$A B = 1$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Graphically:
$∠ R O Q = θ / 2, ∠ R Q O = θ / 2$
Hence, $Δ O Q R$ is isosceles.
$\Rightarrow O R = R Q \Rightarrow B = A$
Analytically:
$tan (θ / 2) = \frac{B sin θ}{A + B cos θ}$
$\Rightarrow \frac{sin (θ / 2)}{cos (θ / 2)} = \frac{2 B sin (θ / 2) cos (θ / 2)}{A + B [2 {cos}^{2} (θ / 2) - 1]}$ ltbr $\Rightarrow A + 2 B {cos}^{2} (θ / 2) - B = 2 B {cos}^{2} (θ / 2) \Rightarrow A = B$
$\Rightarrow A + 2 B {cos}^{2} (θ / 2) - B = 2 B {cos}^{2} (θ / 2) \Rightarrow A = B$

|

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

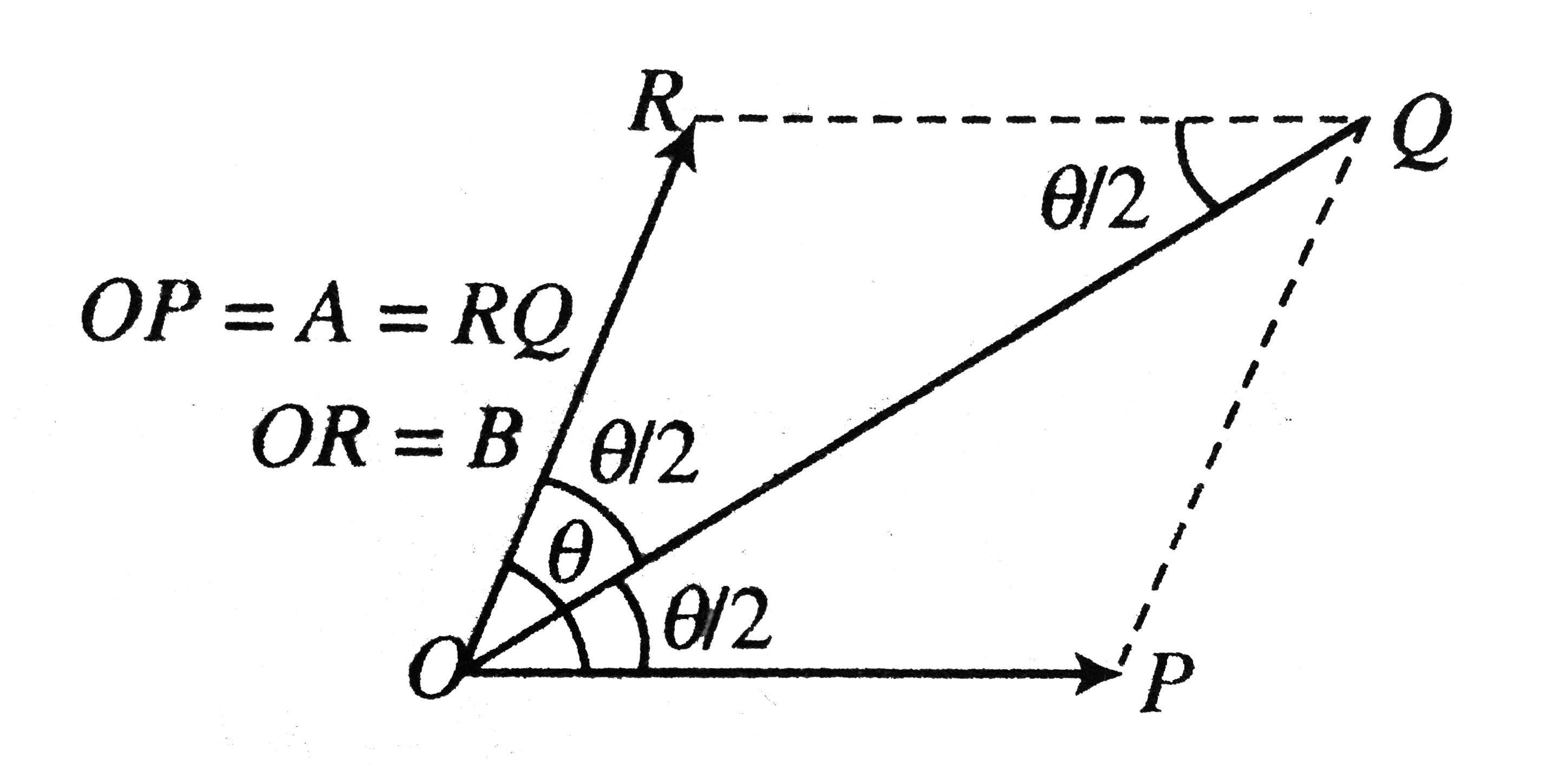
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The angle between two vector A and B is $θ$ . Vector R is the resultant of the two vectors. If R makes an angle $\frac{θ}{2}$ with A, then
A $A = 2 B$
B $A = B / 2$
C $A = B$
D $A B = 1$
Question 2 - Select One
Let the angle between two nonzero vector $\to A and \to B$ is $120^{\circ}$ and its resultant be $\to C$ .
A $C = | A - B |$
B $C < | A - B |$
C $C > | A - B |$
D $C = | A + B |$
Question 3 - Select One
Angular between two vectors $\to A and \to B$ is $θ$ . Resulatnt of the two makes an angle $θ / 2$ with the vector $\to A$ . Select the correct option .
A $A = 1 / B$
B $A = 2 B$
C $A = B$
DNone of these

CENGAGE PHYSICS-VECTORS-Exercise Single Correct

Home
Ask Doubt
Profile