The angle turned by a body undergoing circular motion depends on time as θ=θ0+θ1t+θ2t2. Then the angular acceleration of the body is
θ1
θ2
2θ1
2θ2
The correct Answer is:D
To find the angular acceleration of a body undergoing circular motion, given the angle turned as a function of time, we can follow these steps:
Step 1: Write down the equation for angular displacement
The angle turned by the body is given by:
θ=θ0+θ1t+θ2t2
where θ0, θ1, and θ2 are constants.
Step 2: Differentiate to find angular velocity
To find the angular velocity (ω), we take the first derivative of θ with respect to time t:
dθdt=ddt(θ0+θ1t+θ2t2)
Since θ0 is a constant, its derivative is 0. Thus, we have:
dθdt=θ1+2θ2t
Step 3: Differentiate again to find angular acceleration
Now, we need to find the angular acceleration (α), which is the second derivative of θ with respect to time:
d2θdt2=ddt(θ1+2θ2t)
Again, since θ1 is a constant, its derivative is 0. Therefore, we have:
d2θdt2=2θ2
Step 4: Conclusion
The angular acceleration α is given by:
α=d2θdt2=2θ2
Thus, the angular acceleration of the body is 2θ2.
Final Answer
The correct option is:
Option 4: 2θ2
---
The angle turned by the body is given by:
θ=θ0+θ1t+θ2t2
where θ0, θ1, and θ2 are constants.
To find the angular velocity (ω), we take the first derivative of θ with respect to time t:
dθdt=ddt(θ0+θ1t+θ2t2)
Since θ0 is a constant, its derivative is 0. Thus, we have:
dθdt=θ1+2θ2t
Now, we need to find the angular acceleration (α), which is the second derivative of θ with respect to time:
d2θdt2=ddt(θ1+2θ2t)
Again, since θ1 is a constant, its derivative is 0. Therefore, we have:
d2θdt2=2θ2
The angular acceleration α is given by:
α=d2θdt2=2θ2
The correct option is:
Option 4: 2θ2
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
If angular velocity of a disc depends an angle rotated θ as ω=θ2+2θ, then its angular acceleration α at θ=1 rad is :
View SolutionA solid body rotates about a stationary axis so that the rotation angle θ varies with time as θ=6t−2t3 radian. Find
(a) the angular acceleration at the moment when the body stops and
(b) the average value of angular velocity and angular acceleration averaged over the time interval between t=0 and the complete stop.
View SolutionA solid body rotates about a stationary axis accordig to the law θ=6t−2t3. Here θ, is in radian and t in seconds. Find
(a). The mean values of thhe angular velocity and angular acceleration averaged over the time interval between t=0 and the complete stop.
(b). The angular acceleration at the moment when the body stops.
Hint: if y=y(t). then mean/average value of y between t1 and t2 is <y≥(∫t2t1y(t)dt))t2−t1
View SolutionThe angular position of a point over a rotating flywheel is changing according to the relation, θ=(2t3−3t2−4t−5) radian. The angular acceleration of the flywheel at time, t = 1 s is
View SolutionIntegrate the following functions
∫θ2θ1dθθ−θ0
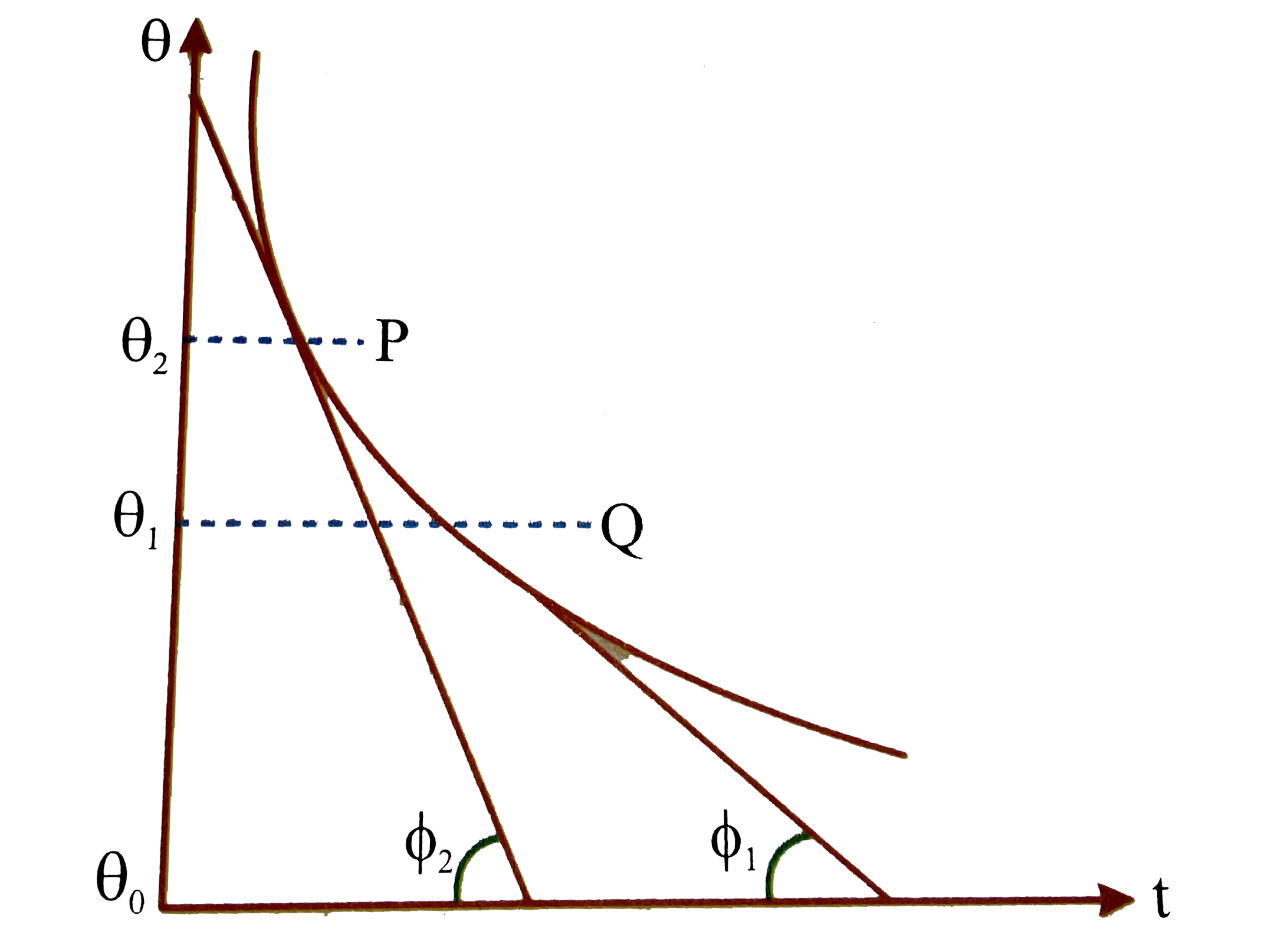
View SolutionA body cools in a surrounding which is at constant temperature of θ0. Assume that it obeys Newton's law of colling. Its temperature θ is plotted against time t. Tangents are drawn to the curve at the points P(θ=θt) and Q(θ=θ2). These tangents meet the time axis at angles of ϕ2 and ϕ1, as shown
View SolutionProve that: sin2θ1+cos2θ=tanθ
View SolutionProve that: sin2θ1+cos2θ=tanθ
View SolutionSolve the following equation: tanθ+tan2θ+tan3θ=0
View Solutioncosθ+sinθ−sin2θ=12,0<θ<π2
View Solution
