A body cools in a surrounding which is at constant temperature of θ0. Assume that it obeys Newton's law of colling. Its temperature θ is plotted against time t. Tangents are drawn to the curve at the points P(θ=θt) and Q(θ=θ2). These tangents meet the time axis at angles of ϕ2 and ϕ1, as shown
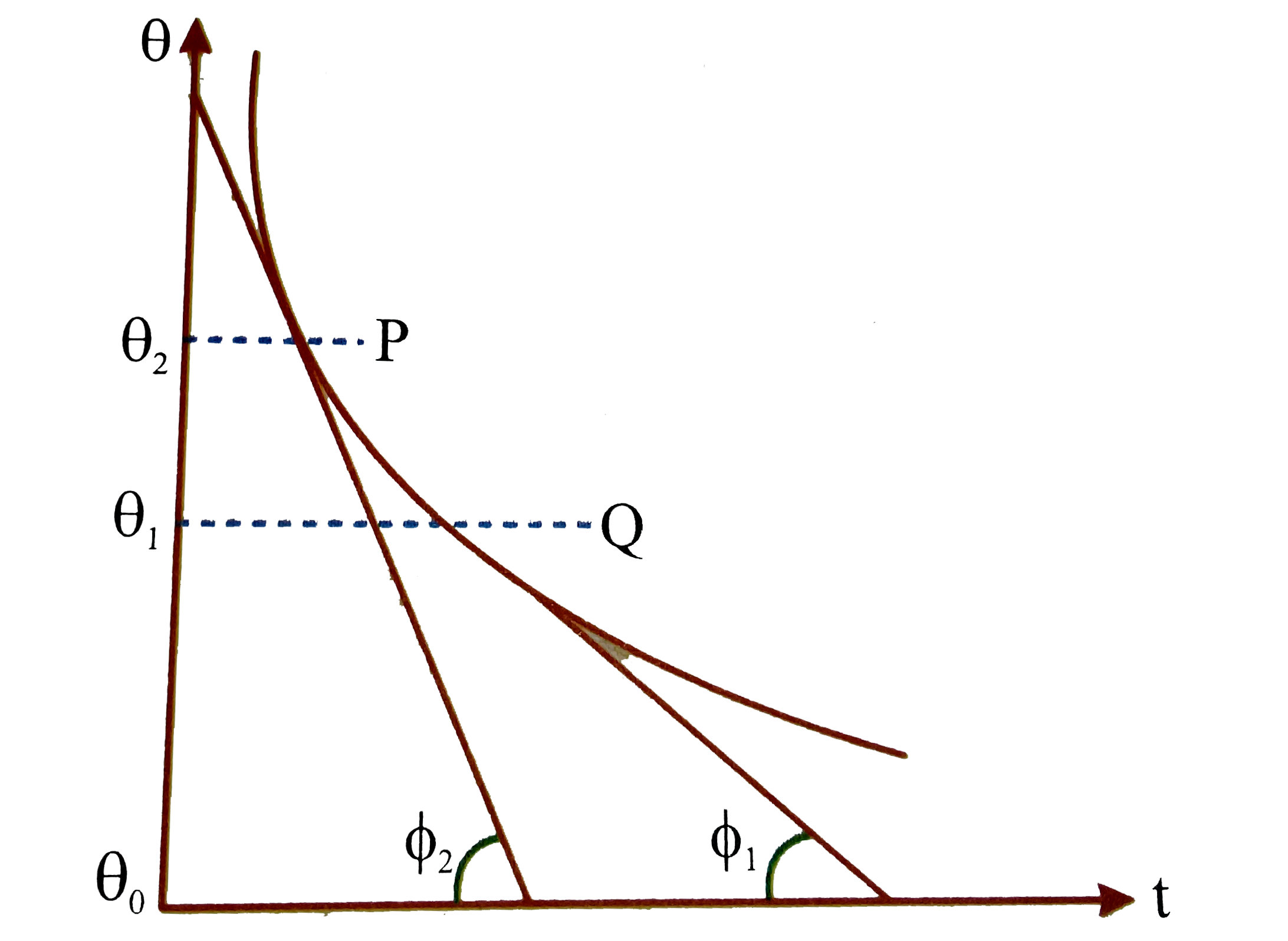
tanϕ2tanϕ1=θ1−θ0θ2−θ0
tanϕ2tanϕ1=θ2−θ0θ1−θ0
tanϕ1tanϕ2=θ1θ2
tanϕ1tanϕ2=θ2θ1
The correct Answer is:B
Newton's law of cooling implies that rate of cooling is proportional to temperature difference if the temperature difference between body and surrounding is small.
Then , (−dθdt)2=tanϕ2α(θ2−θ0) and
(dθdt)1=tanϕ1α(θ1−θ0)⇒tanϕ2tanϕ1=(θ2−θ0θ1−θ0)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -03
10 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
36 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A body with an initial temperature θ1 is allowed to cool in a surrounding which is at a constant temperature of θ0(θ<θ1) Assume that Newton's law of cooling is obeyed Let k= constant The temperature of the body after time t is best experssed by .
View SolutionFind the slopes of the tangent and the normal to the curve x=a(θ−sinθ) , y=a(1+cosθ) at θ=−π/2
View SolutionFind the slopes of the tangent and the normal to the curve x=a(θ−sinθ), y=a(1−cosθ) at θ=π/2
View SolutionThe tangents to the curve x=a(θ−sinθ),y=a(1+cosθ) at the points θ=(2k+1)π,k∈Z are parallel to :
View Solutiontangents are drawn to x2+y2=a2 at the points A(acosθ,asinθ) and B(acos(θ+π3),asin(θ+π3)) Locus of intersection of these tangents is
View SolutionThemperature of a body θ is slightly more than the temperature of the surrounding θ0 its rate of cooling (R) versus temperature of body (θ) is plotted its shape would be .
View SolutionIf a piece of metal is heated to temperature θ and the allowed to cool in a room which is at temperature θ0, the graph between the temperature T of the metal and time t will be closet to
View SolutionFind the equations of the tangent and the normal to the curve x=θ+sinθ , y=1+cosθ at θ=π/2 at indicated points.
View Solutionif the tangent to the curve x=a(θ+sinθ),y=a(1+cosθ) at θ=π3 makes an angle α x=axis then α
View SolutionInstantaneous temperature difference between cooling body and the surroundings obeying Newton's law of cooling is θ. Which of the following represents the variation of In θ with time t?
View Solution