If angular velocity of a disc depends an angle rotated θ as ω=θ2+2θ, then its angular acceleration α at θ=1 rad is :
4 rad/s2
10 rad/s2
12 rad/s2
15 rad/s2
To solve the problem, we need to find the angular acceleration α at θ=1 radian, given that the angular velocity ω is defined as:
ω=θ2+2θ
Step 1: Understand the relationship between angular acceleration and angular velocity
Angular acceleration α is defined as the rate of change of angular velocity with respect to time, which can be expressed as:
α=dωdt
However, since ω is a function of θ, we can use the chain rule to express α in terms of θ:
α=dωdθ⋅dθdt
Step 2: Identify dθdt
The term dθdt is simply the angular velocity ω:
dθdt=ω
Step 3: Substitute into the equation for α
Now we can substitute dθdt into the equation for α:
α=ω⋅dωdθ
Step 4: Find dωdθ
Next, we need to differentiate ω with respect to θ:
ω=θ2+2θ
Differentiating:
dωdθ=ddθ(θ2+2θ)=2θ+2
Step 5: Substitute dωdθ back into the equation for α
Now we substitute dωdθ back into the equation for α:
α=ω⋅(2θ+2)
Step 6: Calculate α at θ=1
First, we need to calculate ω at θ=1:
ω=12+2⋅1=1+2=3
Now substitute θ=1 into the expression for α:
α=3⋅(2⋅1+2)=3⋅(2+2)=3⋅4=12
Thus, the angular acceleration α at θ=1 radian is:
α=12rad/s2
Final Answer
The angular acceleration α at θ=1 radian is 12rad/s2.
---
Angular acceleration α is defined as the rate of change of angular velocity with respect to time, which can be expressed as:
The term dθdt is simply the angular velocity ω:
Now we can substitute dθdt into the equation for α:
Next, we need to differentiate ω with respect to θ:
Now we substitute dωdθ back into the equation for α:
First, we need to calculate ω at θ=1:
The angular acceleration α at θ=1 radian is 12rad/s2.
Topper's Solved these Questions
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-A
11 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-B
10 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - SOLVED EXAMPLES
20 Videos
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - IMPECCABLE
52 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
Similar Questions
the angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
View SolutionThe angle turned by a body undergoing circular motion depends on time as θ=θ0+θ1t+θ2t2. Then the angular acceleration of the body is
View SolutionA uniiform disc of radius r spins with angular velocity ω and angular acceleration α. If the centre of mass of the disc has linear acceleration a, find the magnitude and direction of aceeleration of the point 1,2, and 3.

View SolutionA disc with linear velocity v and angular velocity ω is placed on rough ground. Suppose a and α be the magnitudes of linear and angular acceleration due to friction.
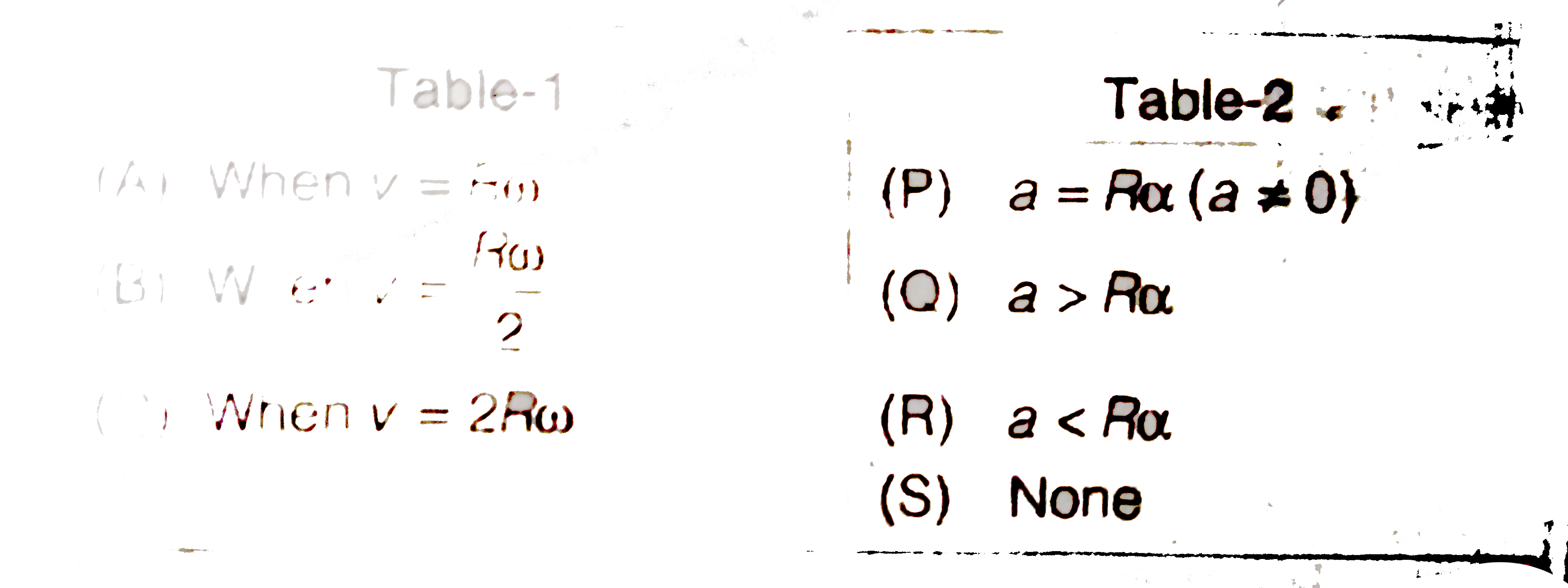

View SolutionA stationary horizontal disc is free to rotate about its axis. When a torque is applied on it its, kinetic energy as a function of θ, where θ is the angle by which it has rotated, is given as kθ. If its moment of inertia is I then the angular acceleration of the disc is :
View SolutionThe angular displacement of a body is given by θ=2t2+5t−3. Find the value of the angular velocity and angular acceleration when t = 2s.
View SolutionIf tan2θtanθ=1,thenθ=
View SolutionA disc of mement of inertia I is rotating due to external torque. Its kinetic energy is equal to Kθ2. Where K is the positive constant. Its angular acceleration at an angle θ will be:
View SolutionA body rotates about a fixed axis with an angular acceleration of 3rad/s2 . The angle rotated by it during the time when its angular velocity increases frm 10 rad/s to 20 rad/s (in radian) is
View SolutionA wheel is rotating with an angular velocity of 3rads−1. If the angular acceleration is 2rads−1 then calculate its angular velocity after 5 second.
View Solution
