The angle which the rough inclined plane makes with the horizontal when the body placed on it just starts sliding down is called
Angle of friction
Angle of repose
Critical angle
Brewster's angle
The correct Answer is:B
To solve the problem, we need to understand the concept of the angle at which a body starts to slide down a rough inclined plane. This angle is known as the critical angle. Let's break down the solution step by step.
1. Understanding the Scenario:
- We have a rough inclined plane making an angle θ with the horizontal.
- A body is placed on this inclined plane.
2. Condition for Sliding:
- The body will start sliding down the inclined plane when the force of gravity acting on it exceeds the maximum static frictional force that can act on it.
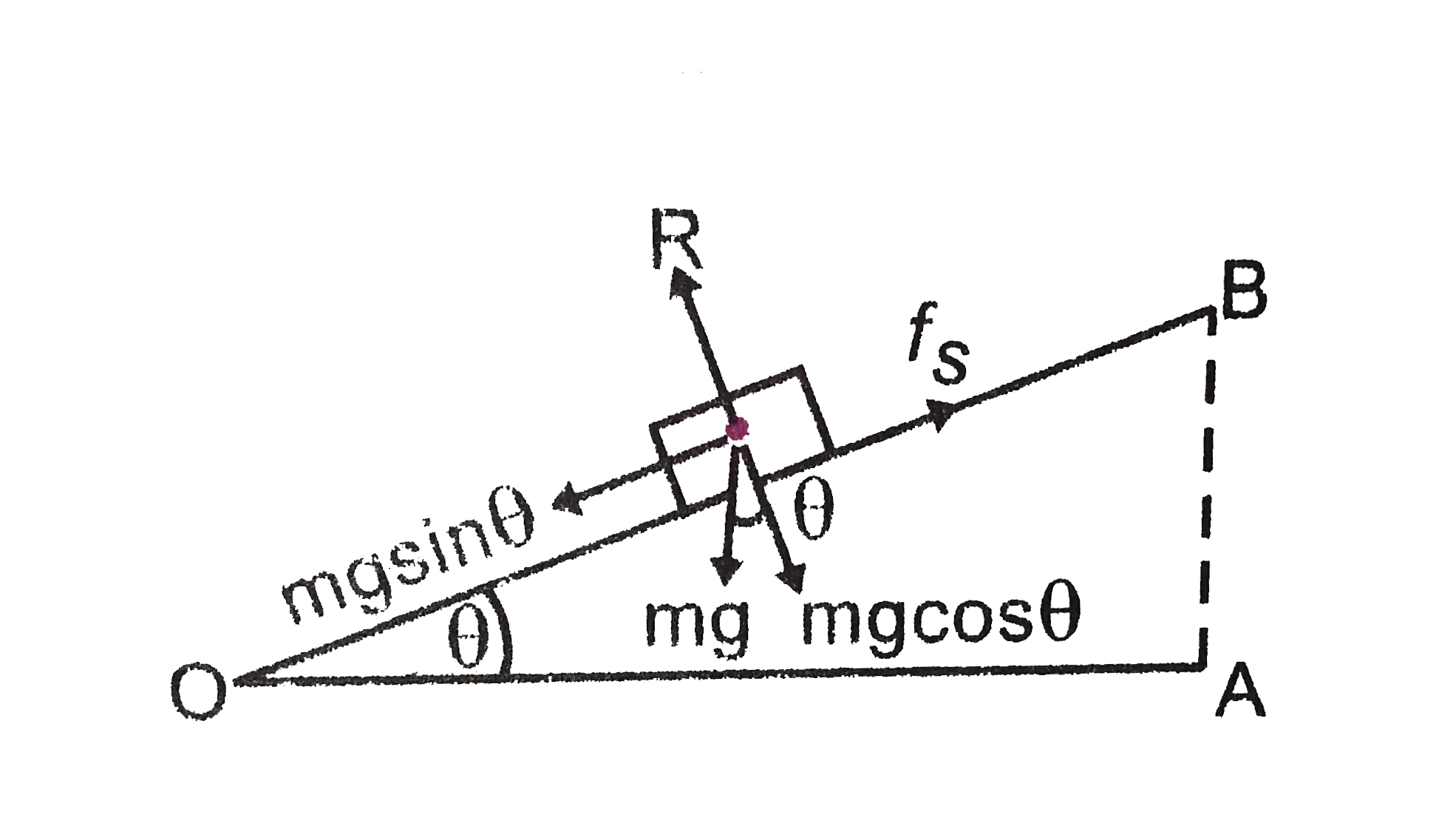
3. Forces Acting on the Body:
- The gravitational force acting downwards can be resolved into two components:
- Perpendicular to the inclined plane: mgcosθ
- Parallel to the inclined plane: mgsinθ
- The frictional force acting up the incline is given by f=μN, where N is the normal force and μ is the coefficient of friction.
4. Normal Force Calculation:
- The normal force N is equal to the perpendicular component of the gravitational force:
N=mgcosθ
5. Frictional Force:
- The maximum static frictional force is:
f=μN=μ(mgcosθ)
6. Setting Up the Equation:
- The body starts to slide when the component of gravitational force parallel to the incline equals the maximum static frictional force:
mgsinθ=μ(mgcosθ)
7. Simplifying the Equation:
- We can cancel mg from both sides (assuming m≠0):
sinθ=μcosθ
8. Finding the Critical Angle:
- Dividing both sides by cosθ:
tanθ=μ
- Therefore, the angle θ at which the body just starts to slide is called the critical angle θc, and we have:
tanθc=μ
9. Conclusion:
- The angle which the rough inclined plane makes with the horizontal when the body placed on it just starts sliding down is called the critical angle.
Final Answer:
The angle is called the critical angle.
- We have a rough inclined plane making an angle θ with the horizontal.
- A body is placed on this inclined plane.
- The body will start sliding down the inclined plane when the force of gravity acting on it exceeds the maximum static frictional force that can act on it.
- The gravitational force acting downwards can be resolved into two components:
- Perpendicular to the inclined plane: mgcosθ
- Parallel to the inclined plane: mgsinθ
- The frictional force acting up the incline is given by f=μN, where N is the normal force and μ is the coefficient of friction.
- The normal force N is equal to the perpendicular component of the gravitational force:
N=mgcosθ
- The maximum static frictional force is:
f=μN=μ(mgcosθ)
- The body starts to slide when the component of gravitational force parallel to the incline equals the maximum static frictional force:
mgsinθ=μ(mgcosθ)
- We can cancel mg from both sides (assuming m≠0):
sinθ=μcosθ
- Dividing both sides by cosθ:
tanθ=μ
- Therefore, the angle θ at which the body just starts to slide is called the critical angle θc, and we have:
tanθc=μ
- The angle which the rough inclined plane makes with the horizontal when the body placed on it just starts sliding down is called the critical angle.
The angle is called the critical angle.
Similar Questions
A cubical block rests on a plane of μ=√3 . The angle through which the plane be inclined to the horizontal so that the block just slides down will be -
View SolutionAssertion: A body slides down an inclined plane if the angle of friction is more than the angle of the inclined plane with the horizontal.
Reason : When the angle of inclination is equal to the angle of friction, the component of weight parallel to the plane is just sufficient to overcome the frictional force.
View Solution
Knowledge Check
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ
If the angle of inclination of the inclined plane is sin−1(12) when the body just starts sliding find the angle of repose and coefficient of static friction between the body and the inclined plane.
View SolutionStarting from rest, the time taken by a body sliding down on a rough inclined plane at 45∘ with the horizontal is twice the time taken to travel on a smooth plane of same inclination and same distance. Then, the coefficient of kinetic friction is
View SolutionA rectangular box lies on a rough inclined surface . The coefficient of friction between the surface and the box is μ. Let the mass of the box be m .
(a) At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane ?
(b) What is the force acting on the box down the plane , if the angle of inclination of the plane is increased to α>θ ?
(c) What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed ?
(d) What is the force needed to be applied upwards along the plane to make the box move up the plane with acceleration a ?
View SolutionA body is pushed up on a rough inclined plane making an angle 30∘ to the horizontal. If its time of ascent on the plane is half the time of its descent, find coefficient of friction between the body and the incined plane.
View SolutionA mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
View SolutionA uniform disc of mass m and radius R is rolling up a rough inclined plane which makes an angle of 30∘ with the horizontal. If the coefficients of static and kinetic friction are each equal to μ and the only force acting are gravitational and frictional, then the magnitude of the frictional force acting on the disc is and its direction is .(write up or down) the inclined plane.
View SolutionA body of mass 5×10−3 kg is launched upon a rough inclined plane making an angle of 30∘ with the horizontal. Obtain the coefficient of friction between the body and the plane if the time of ascent is half of the time of descent.
View Solution
