A cubical block rests on a plane of μ=√3 . The angle through which the plane be inclined to the horizontal so that the block just slides down will be -
30∘
45∘
60∘
75∘
The correct Answer is:C
To solve the problem of determining the angle at which a cubical block will just slide down an inclined plane with a coefficient of friction μ=√3, we can follow these steps:
Step 1: Understand the Forces Acting on the Block
- The block experiences two main forces: its weight (mg) acting downward and the normal force (N) acting perpendicular to the inclined plane.
- The weight can be resolved into two components: one parallel to the incline (mgsinθ) and one perpendicular to the incline (mgcosθ).
Step 2: Write the Expression for the Forces
- The frictional force (Ff) acting against the motion of the block is given by:
Ff=μN
- The normal force can be expressed as:
N=mgcosθ
- Therefore, the frictional force becomes:
Ff=μmgcosθ
Step 3: Set Up the Inequality for Motion
- For the block to just start sliding down, the component of the gravitational force along the incline must equal the frictional force:
mgsinθ=Ff
- Substituting the expression for the frictional force, we have:
mgsinθ=μmgcosθ
Step 4: Simplify the Equation
- We can cancel mg from both sides (assuming mg≠0):
sinθ=μcosθ
Step 5: Substitute the Value of μ
- Given μ=√3, we substitute this into the equation:
sinθ=√3cosθ
Step 6: Divide Both Sides by cosθ
- This gives:
tanθ=√3
Step 7: Find the Angle θ
- The angle θ for which tanθ=√3 is:
θ=60∘
Conclusion
- Therefore, the angle through which the plane must be inclined for the block to just slide down is θ=60∘.
- The block experiences two main forces: its weight (mg) acting downward and the normal force (N) acting perpendicular to the inclined plane.
- The weight can be resolved into two components: one parallel to the incline (mgsinθ) and one perpendicular to the incline (mgcosθ).
- The frictional force (Ff) acting against the motion of the block is given by:
Ff=μN
- The normal force can be expressed as:
N=mgcosθ
- Therefore, the frictional force becomes:
Ff=μmgcosθ
- For the block to just start sliding down, the component of the gravitational force along the incline must equal the frictional force:
mgsinθ=Ff
- Substituting the expression for the frictional force, we have:
mgsinθ=μmgcosθ
- We can cancel mg from both sides (assuming mg≠0):
sinθ=μcosθ
- Given μ=√3, we substitute this into the equation:
sinθ=√3cosθ
- This gives:
tanθ=√3
- The angle θ for which tanθ=√3 is:
θ=60∘
- Therefore, the angle through which the plane must be inclined for the block to just slide down is θ=60∘.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -B) objective type questions (one option is correct)
59 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -C) objective type questions (More than one options are correct)
21 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - TRY YOURSELF
69 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
The angle which the rough inclined plane makes with the horizontal when the body placed on it just starts sliding down is called
View SolutionThe coefficient of static friction between a block of mass m and an incline is μs=0.3, a. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle θ2 with the horizontal, find the frictional force on the block.
View Solution
Knowledge Check
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ
A block is placed on a smooth inclined plane at an angle 'θ' to the horizontal. The acceleration must the plane be moved horizontally so that the block to fall freely is
View SolutionA block of mass 5 kg is placed on a rough inclined plane. The inclination of the plane is gradually increased till the block just begins to slide down. The inclination of the plane is than 3 in 5. The coefficient of friction between the block and the plane is (Take, g=10m/s2)
View SolutionA block is placed on the top of a plane inclined at 37∘ with horizontal. The length of the plane is 5m. The block slides down the plane and reaches the bottom.
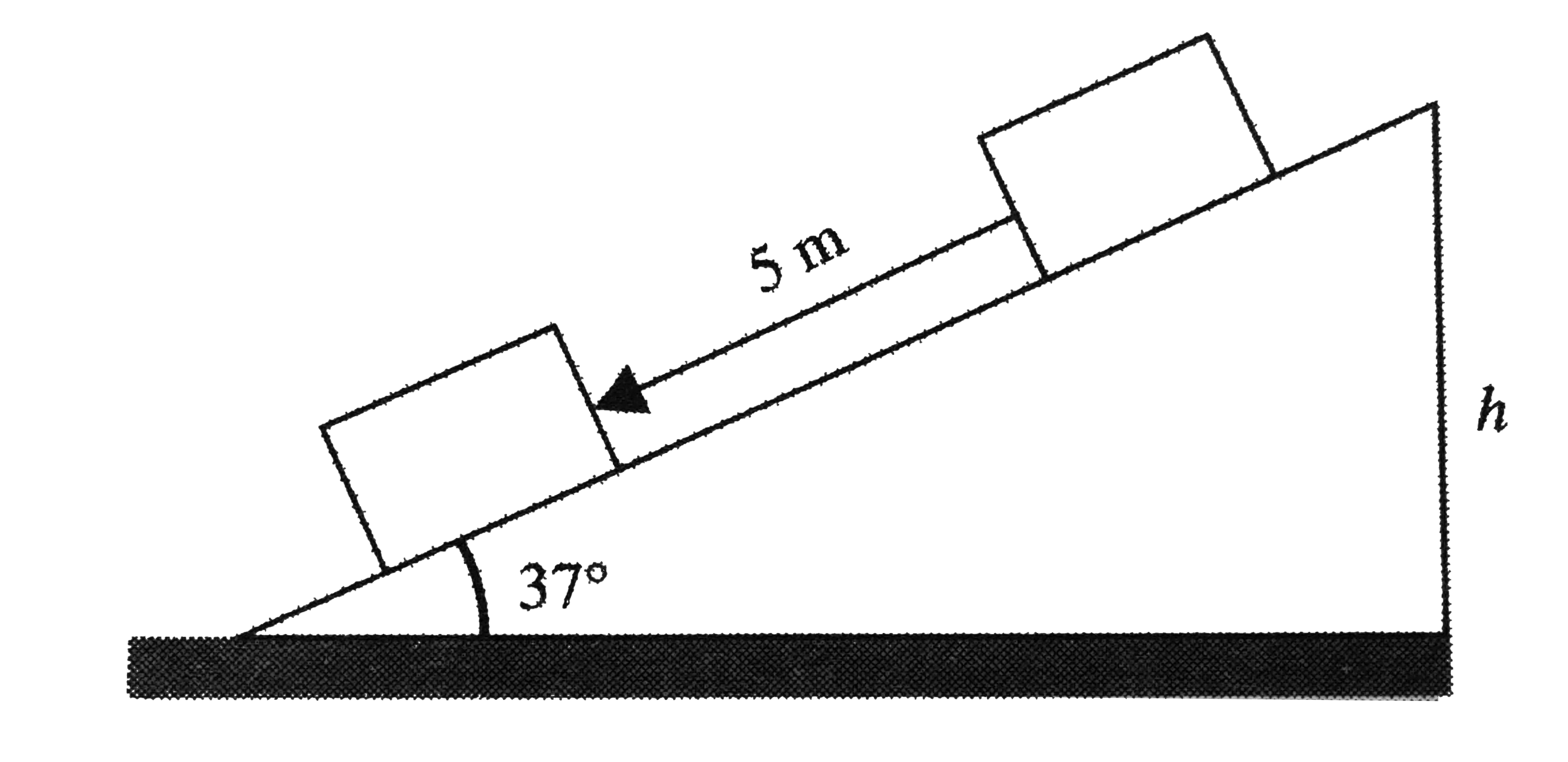
a. Find the speed of the block at the bottom if the inclined plane is smooth.
b. Find the speed of the block at the bottom if the coefficient of friction is 0.25.
View SolutionA block is at rest on an inclined plane making an angle α with the horizontal. As the angle of the incline is increased the block start slipping when the angle of inclination becomes θ then coefficient of friction is equal to
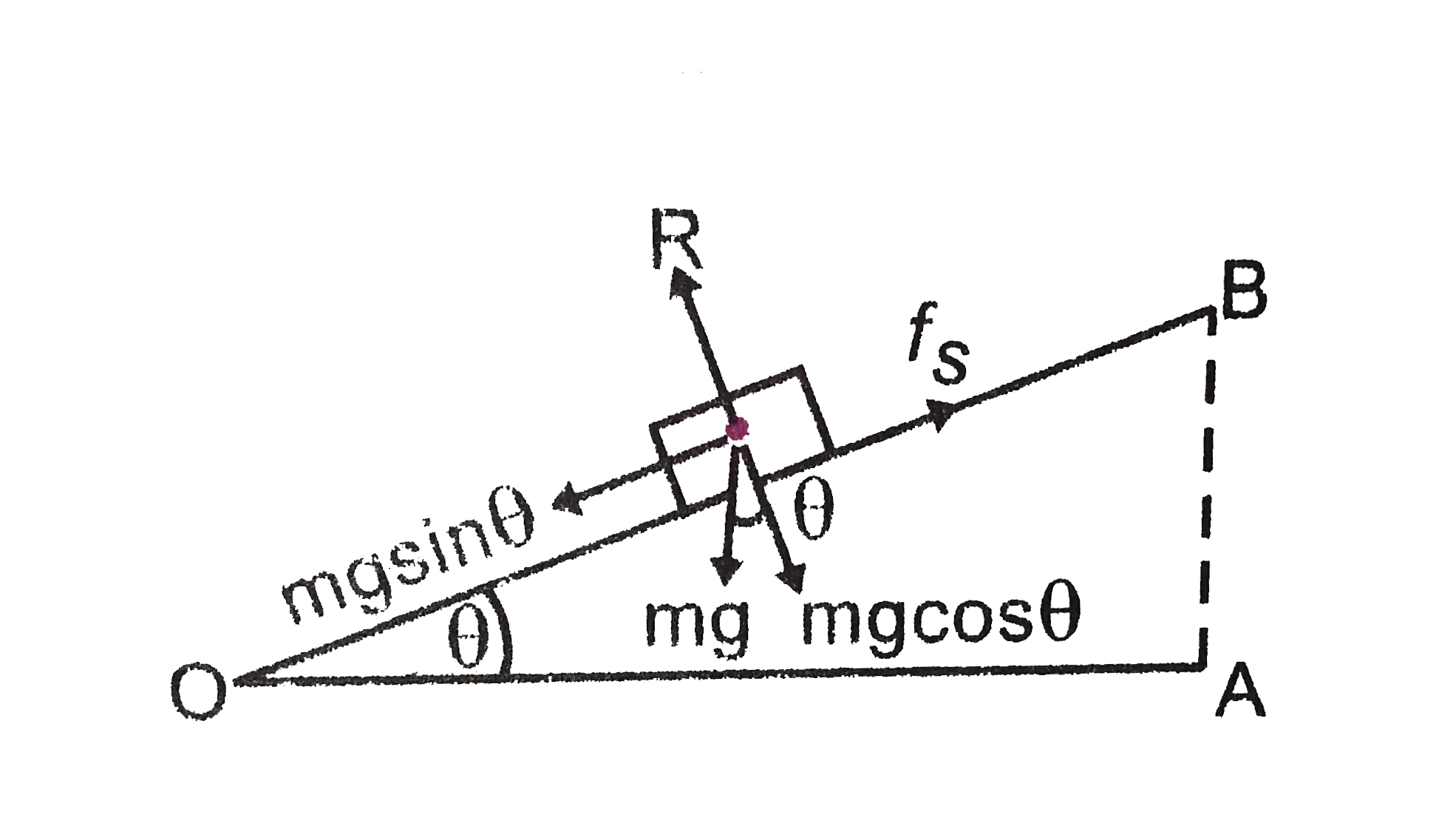
View SolutionA mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View Solution
