A mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
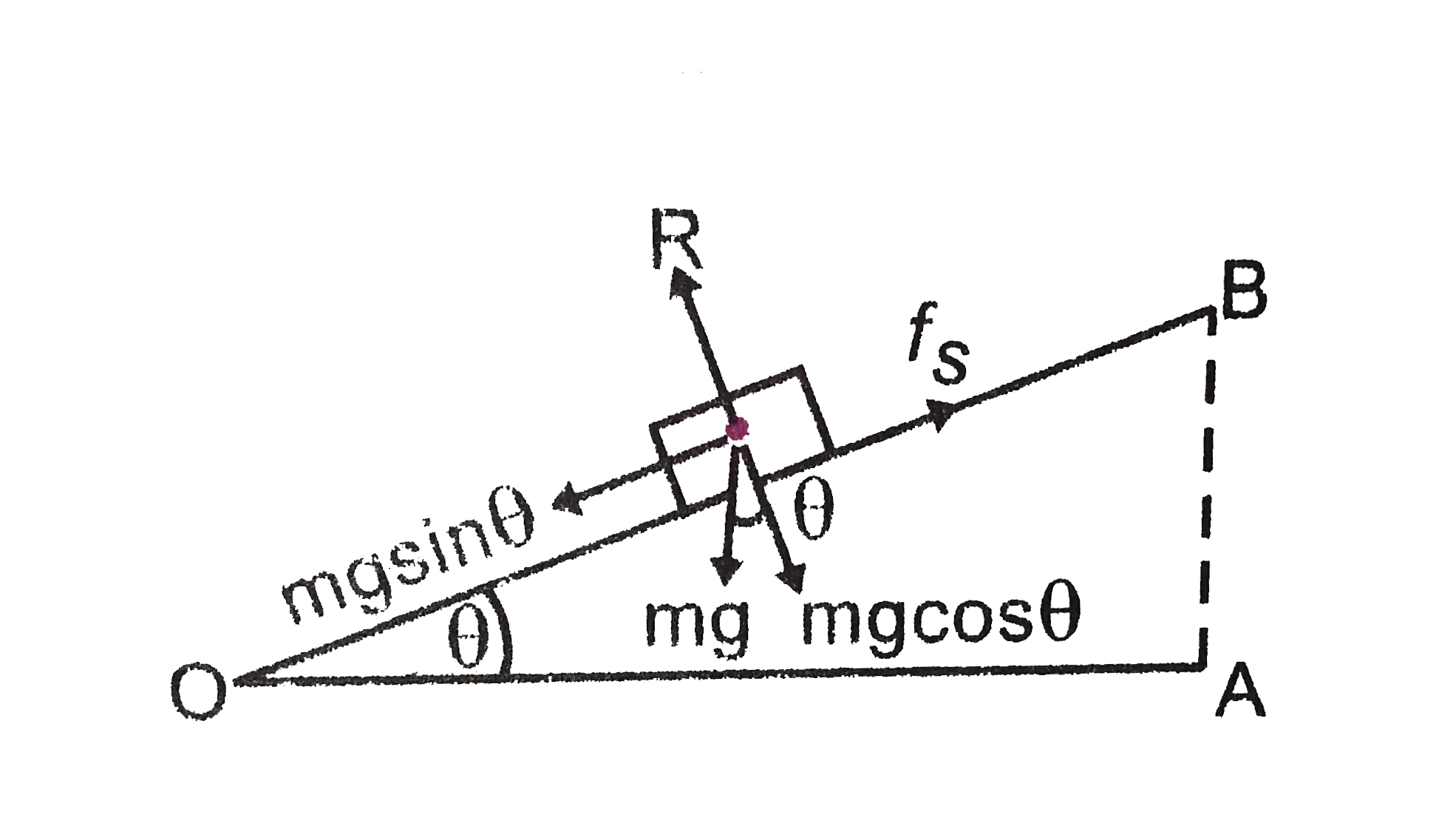
The forces acting on a block of mass m at rest on an inclined plane are (i) the weight mg acting vertically downwards (ii) the normal force N of the plane on the block , and (iii) the static frictional force fs opposing the impending motion. In equilibrium , the resulatant of these forces must be zero. Resolving the weight mg along the two directions shown, we have
m g sin θ = fs , m g cosθ = N
As θ increases , the self-adjusting frictional force fs increases until at θ = θmax, fs achieves its maximum value , (fs)max = μsN.
Therefore , tan<θmax=μs or θmax = tan−1μs
When θ becomes just a little more than θmax , there is a small net force on the block and it begins to slide. Note that θmax depends only on μs and is independent of the mass of the block.
For θmax = 15∘
μs = tan 15∘
= 0.27
Topper's Solved these Questions
Similar Questions
Give the magnitude and direction of the net force acting on
(a) a drop of rain falling down with a constant speed
(b) a cork of mass 10 g floating on water
(c) a kite skillfully held stationary in the sky
(d) a car moving with a constant velocity of 30kh/h on a rough road
(e) a high speed electron in space free from all gravitational objects and free of electric and magnetic fields.
View SolutionEstimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP. Take the diameter of an oxygen molecule to be 3Å.
View SolutionExplain why (a) the blood pressure is humans is greater at the feet than at the brain.
(b) Atmospheric pressure at a height of about 6 km decreases to nearly half its value at the sea level through the 'height' of the atmospheric is more than 100 km.
(c) Hydrostatic pressure is a scalar quantity even though pressure is force divided by area , and force is a vector.
View SolutionA mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?

View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30^(@) with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block of mass 4kg rests on a rough horizontal plane. The plane is gradually inclined until at an angle θ=60∘ , with the vertical, the mass just begins to side. What is the coefficient of static friction between the block and the plane?
View SolutionA mass of 4kg rests on a horizontal plane the plane is gradually inclined unitl at an angle =15 with the horizontal the mass just begins to slide what is the coefficient of static friction bwtween the block and the surface
View SolutionA mass of 4kg rests on a horizontal plane the plane is gradually inclined unitl at an angle =15 with the horizontal the mass just begins to slide what is the coefficient of static friction bwtween the block and the surface
View SolutionSee Fig. A mass of 4 kg rests on a horizontal plane. The plane is gradually inclined until at an angle θ=15∘ with the horizontal, the mass just begins to slide. What is the coefficient of static friction between the block and the surface ?
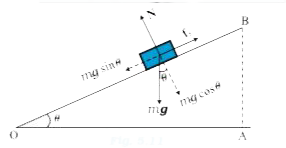
View SolutionSee Fig. A mass of 4 kg rests on a horizontal plane. The plane is gradually inclined until at an angle θ=15∘ with the horizontal, the mass just begins to slide. What is the coefficient of static friction between the block and the surface ?
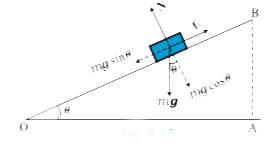
View SolutionSee Fig. A mass of 4 kg rests on a horizontal plane. The plane is gradually inclined until at an angle θ=15∘ with the horizontal, the mass just begins to slide. What is the coefficient of static friction between the block and the surface ?
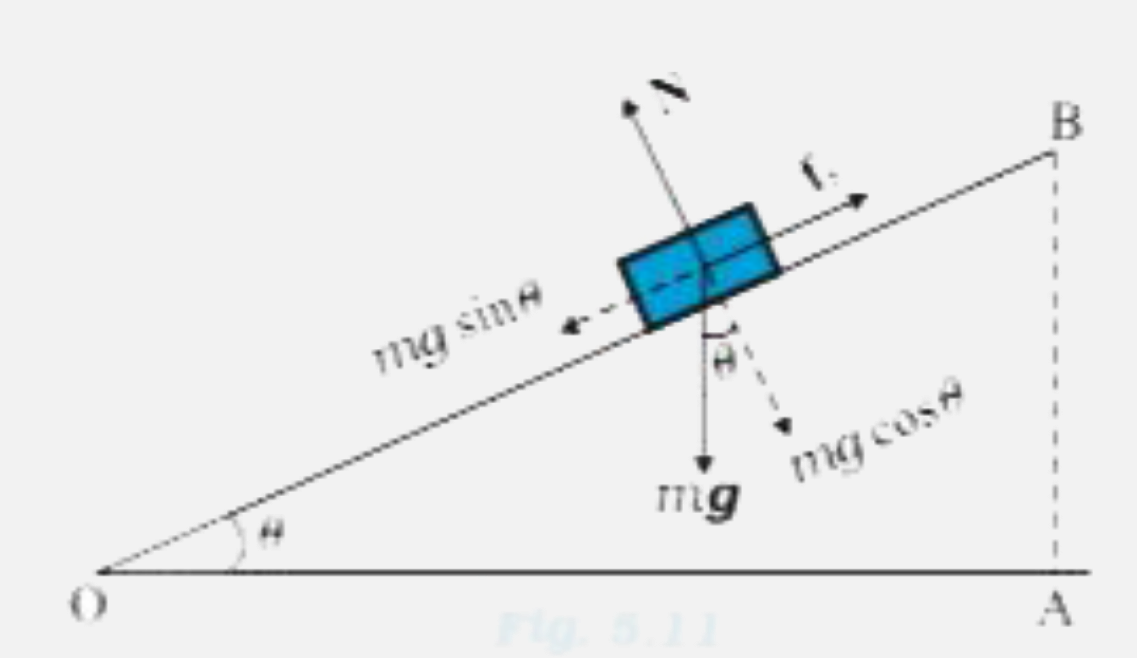
View SolutionA mass of 4 kg rests on a horizontal plane. The plane is gradually inclined until at an angle 0=15∘ with the horizontal, the mass just begins to slide. What is the coefficient of static friction between the block and the surface
View SolutionA mass of 4 kg rests on a horizontal plane. The plane is gradually inclined until an angle θ=15∘ with the horizontal and the mass begins to slide. What is the coefficient of static friction between the block and the surface ?
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View Solution
