The angular displacement of a simple pendulum is increased from 2∘ to 4∘. Its frequency of oscillation
remains same
is doubled
is halved
is quadrupled
The correct Answer is:A
Step by step video, text & image solution for The angular displacement of a simple pendulum is increased from 2^(@) to 4^(@). Its frequency of oscillation by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Oscillation Of Simple Pendulum
View SolutionIdentify wrong statements among the following
The greater the mass of a pendulum bob, the shorter is its frequency of oscillation
A simple pendulum with a bob of mass M swings with an angular amplitude of 40∘. When its angular amplitude is20∘, the tension in the string is less than Mgcos20∘. (3) The fractional change in the time period of a pendulum on changing the temperature is independent of the length of the pendulum.
As the length of a simple pendulum is increased, the maximum velocity of its bob during its oscillation will also decreases.
View Solution
Knowledge Check
The amplitude of oscillation of a simple pendulum is increased from 1∘ to 4∘. Its maximum acceleration changes by a factor of
A14B12C2D4The time period of a simple pendulum is 0.2 s. What is its frequency of oscillation?
A0.5 HzB5 HzC50 HzD1 HzIF the length of a simple pendulum is increased, its maximum velocity during oscillation
AdecreasesBincreasesCremains sameDis zero
The oscillation of a simple pendulum is graphically represented as follows. Determine the
(a) time period (b) frequency (c) amplitude
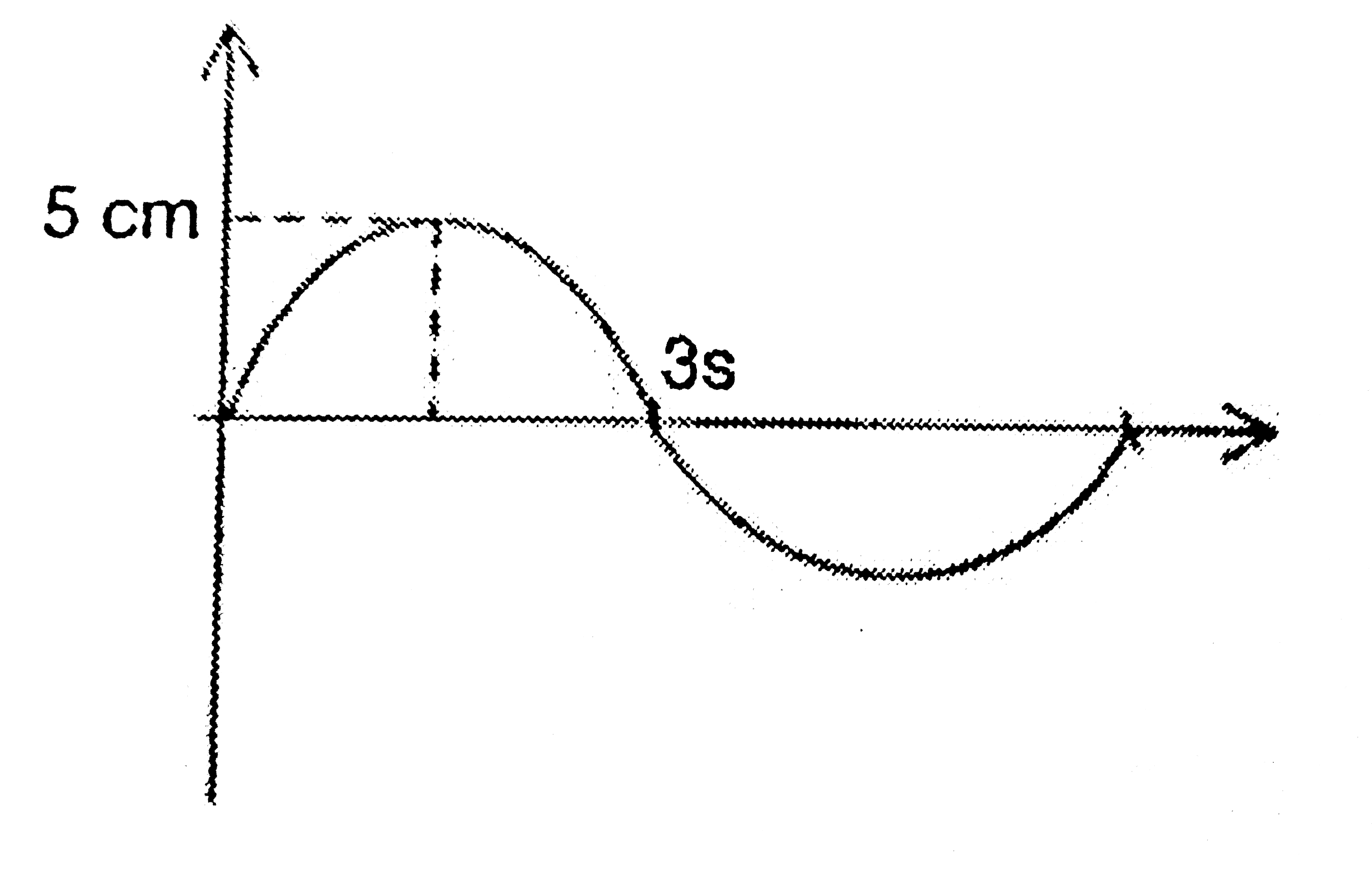
View SolutionLet θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension in the string is mgcosθ
View SolutionLet θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension in the string is mgcosθ
View SolutionWhen the length of a simple pendulum is increased by 36 cm, its time period of oscillation is found to increase by 25 %. The initial length of the simple pendulum 1s (Acceleration due to gravity= 9.8ms−2)
View SolutionThe instantaneous displacement of a simple pendulum oscillator is given by x=Acos(ωt+π4)Its speed will be maximum at time
View Solution
