The approximate formula expressing the mutual inductance of two thin co-axial loops of the same radius a when their centres are separated by a distance l, with $l > > a$ is:

$\frac{1}{2} \frac{μ_{0} π a^{4}}{l^{3}}$

$\frac{1}{2} \frac{μ_{0} a^{4}}{l^{3}}$

$\frac{μ_{0}}{4 π}, \frac{π a^{2}}{l^{2}}$

$\frac{μ_{0}}{π} . \frac{a^{4}}{l^{3}}$

Text Solution

Verified by Experts

Let I= current in one loop This magnetic flux at the centre of the other co-axial loop at a distance l from the centre of the first loop is
$B = \frac{μ_{0}}{4 π} \frac{2 I . π a^{2}}{{(a^{2} + l^{2})}^{3 / 2}}$ …..(1)
Where $p_{m} = I . π a^{2}$
=magnetic moment of loop
The flux through the other loop is
$ϕ_{12} = B π a^{2}$
$= \frac{μ_{0}}{4 π} . \frac{2 π a^{2} I}{{(a^{2} + l^{2})}^{3 / 2}} π a^{2}$
or $\frac{ϕ_{12}}{I} = \frac{μ_{0}}{4 π} . \frac{2 π^{2} a^{4}}{2 {(a^{2} + l^{2})}^{3 / 2}} = \frac{μ_{0} π a^{4}}{2 {(a^{2} + l^{2})}^{3 / 2}}$
$∵ ϕ_{12} = M_{12} I$
$∴ M_{12} = \frac{ϕ_{12}}{I} = \frac{1}{2} \frac{μ_{0} π a^{4}}{l^{3}} ∵ a < < 1$

Updated on:21/07/2023

The approximate formula expressing the formula of mutual inductance of two coaxial loops of the same redius $a$ when their centers are separated by a distance $l$ with $l > > a$ is
A $\frac{1}{2} \frac{μ_{0} π a^{4}}{l^{3}}$
B $\frac{1}{2} \frac{μ_{0} a^{4}}{l^{2}}$
C $\frac{μ_{0}}{4 π} \frac{π a^{4}}{l^{2}}$
D $\frac{μ_{0}}{π} \frac{a^{4}}{l^{3}}$
What is the mutual inductance of a two-loop system as shown with centre separation l

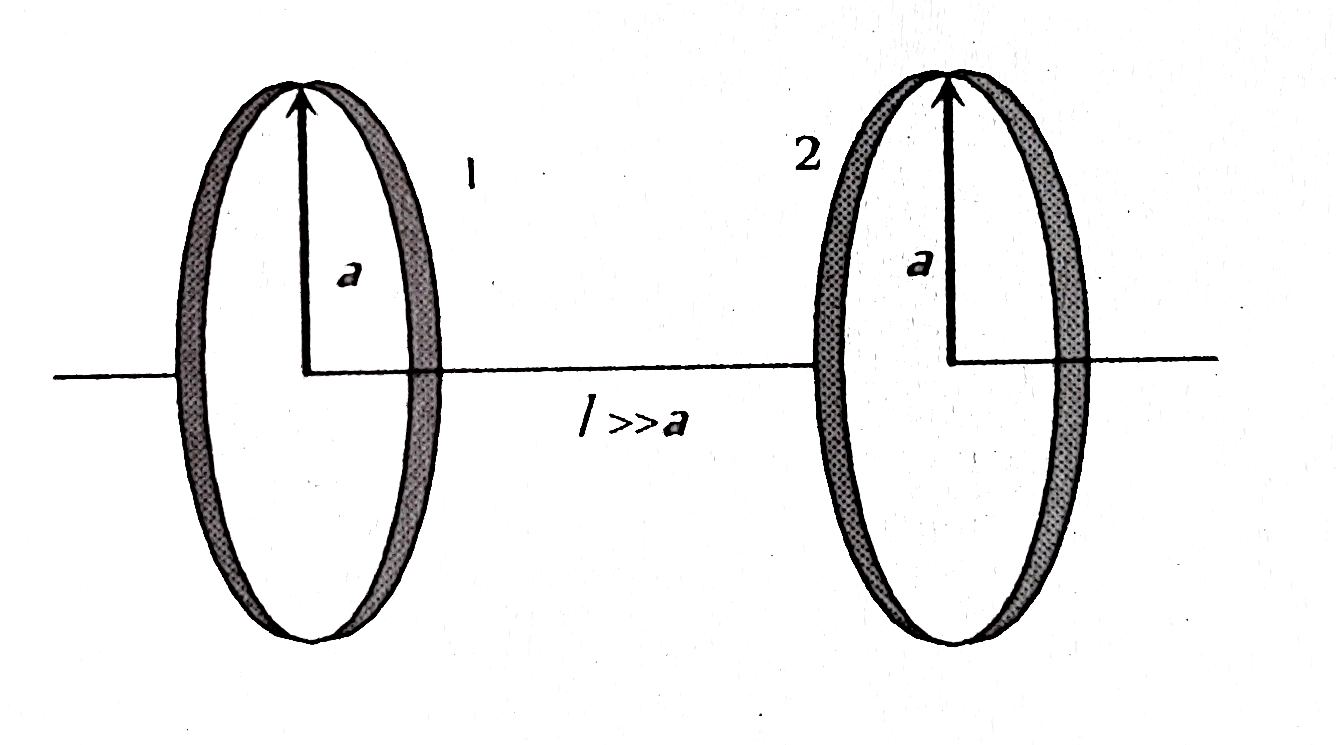A $\frac{μ_{0} π a^{4}}{8 l^{3}}$
B $\frac{μ_{0} π a^{4}}{4 l^{3}}$
C $\frac{μ_{0} π a^{4}}{6 l^{3}}$
D $\frac{μ_{0} π a^{4}}{2 l^{3}}$
What is the mutual inductance of a two-loop system as shown with centre separation $l$ ?

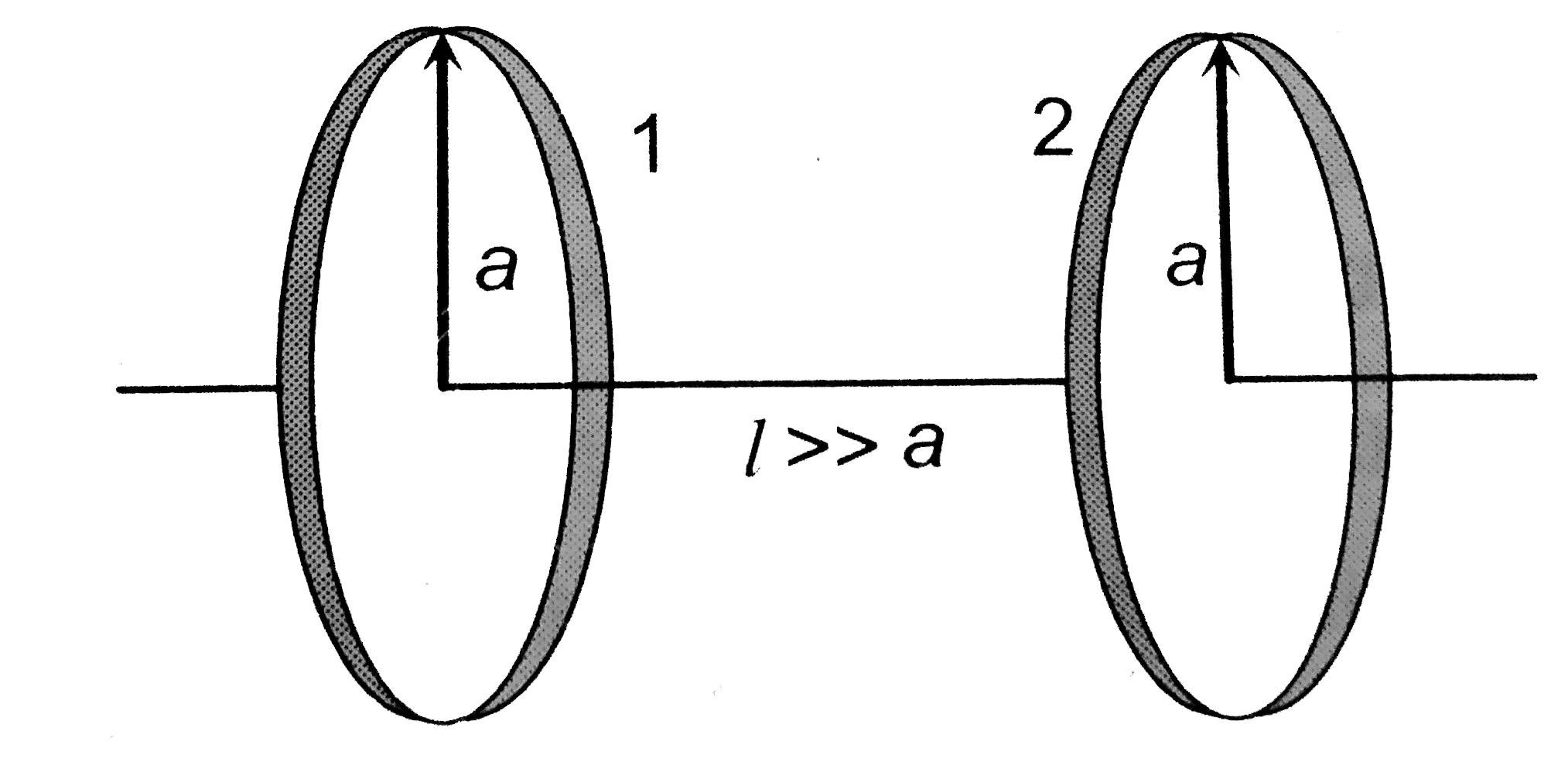A $\frac{μ_{0} π a^{4}}{8 l^{3}}$
B $\frac{μ_{0} π a^{4}}{4 l^{3}}$
C $\frac{μ_{0} π a^{4}}{6 l^{3}}$
D $\frac{μ_{0} π a^{4}}{(2 l^{3})}$