The approximate formula expressing the formula of mutual inductance of two coaxial loops of the same redius a when their centers are separated by a distance l with l>>a is
12μ0πa4l3
12μ0a4l2
μ04ππa4l2
μ0πa4l3
The correct Answer is:A
To find the approximate formula for the mutual inductance M of two coaxial loops of the same radius a when their centers are separated by a distance l (with l≫a), we can follow these steps:
Step 1: Understanding the Magnetic Field Due to One Loop
The magnetic field B at a distance l from the center of a single loop carrying a current I is given by the formula:
B=μ0I4π⋅2πa2(l2+a2)3/2
Where:
- μ0 is the permeability of free space,
- a is the radius of the loop,
- l is the distance from the center of the loop.
Step 2: Calculate the Magnetic Flux Through the Second Loop
The magnetic flux Φ through the second loop due to the magnetic field from the first loop is given by:
Φ=B⋅A
Where A is the area of the second loop, which is πa2. Substituting the expression for B:
Φ=(μ0I4π⋅2πa2(l2+a2)3/2)⋅πa2
Step 3: Simplifying the Expression for Flux
Now we can simplify the expression for magnetic flux:
Φ=μ0I4π⋅2πa2⋅πa2(l2+a2)3/2
This simplifies to:
Φ=μ0Iπa42(l2+a2)3/2
Step 4: Mutual Inductance Definition
The mutual inductance M is defined as the ratio of the magnetic flux through one loop to the current in the other loop:
M=ΦI
Substituting the expression for Φ:
M=μ0Iπa42(l2+a2)3/2I
Step 5: Final Expression for Mutual Inductance
The I cancels out, leading to:
M=μ0πa42(l2+a2)3/2
Step 6: Approximation for Large l
Since l≫a, we can approximate (l2+a2)3/2≈l3. Therefore, we can simplify M:
M≈μ0πa42l3
Final Result
Thus, the approximate formula for the mutual inductance M of two coaxial loops of the same radius a when their centers are separated by a distance l (with l≫a) is:
M≈μ0πa42l3
---
The magnetic field B at a distance l from the center of a single loop carrying a current I is given by the formula:
- μ0 is the permeability of free space,
- a is the radius of the loop,
- l is the distance from the center of the loop.
The magnetic flux Φ through the second loop due to the magnetic field from the first loop is given by:
Now we can simplify the expression for magnetic flux:
The mutual inductance M is defined as the ratio of the magnetic flux through one loop to the current in the other loop:
The I cancels out, leading to:
Since l≫a, we can approximate (l2+a2)3/2≈l3. Therefore, we can simplify M:
Thus, the approximate formula for the mutual inductance M of two coaxial loops of the same radius a when their centers are separated by a distance l (with l≫a) is:
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (multiple Correct )
7 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (subjective)
7 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
Mutual inductance of two coils depends on their self inductance L1 and L2 as :
View SolutionFind the mutual inductance between two coaxial loops of radii R and r (R gtgt r) with separation between the centre x.
View SolutionDefine mutual inductance between a pair of coils. Derive expression for the mutual inductance of two long coaxial solenoids of same length wound one over the other.
View SolutionTwo circular coils have their centres at the same point. The mutual inductance between them will be maximum when their axes
View SolutionCalculate the position of centre of mass of a system consisting of two particles of masses m_1 and m_2 separated by a distance L apar, from m_1?
View SolutionShow that if two inductors with equal inductance L are connected in parallel then the equivalent inductance of combination is L/2.The inductors are separated by a large distance.
View SolutionAnswer the following:
(a) Define mutual inductance and write its S.I. unit.
(b) A square loop of side a carrying a current I2 is kept at distance x from an infinitely long straight wire carrying a current I1 as shown in the figure. Obtain the expression for the resultant force on the loop.

View Solution(a) State Lanz's law. Give one example to illustrate this law. "The Lenz's law is a consequence of the principle of conservation of energy." Justify this statement.
(b) Deduce a expression for the mutual inductance of two long coaxial solenoids but having different radii and different number of turns.
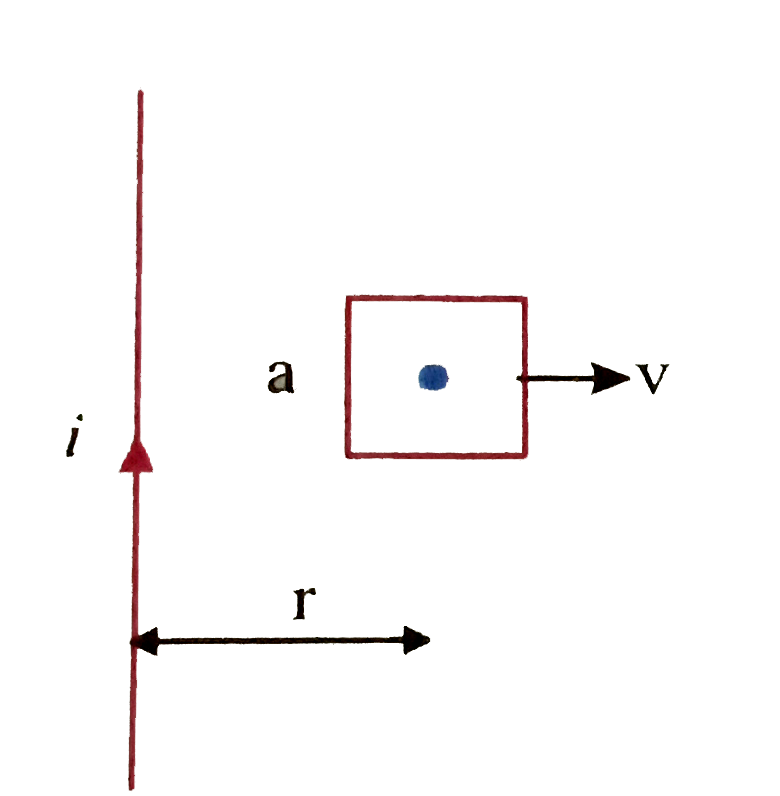
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
View SolutionTwo separated sources emit sinusoidal travelling waves but have the same wavelength λ and are in phase at their respective sources . One travels a distance l1 to get to the observeration point while the other travels a distance l2 . The amplitude is minimum at the observation point , l1−l2 is an
View Solution
