The arms of a vertical U tube of uniform inner cross section contains mercury. In one of the arms of the tube, water column of length 8 cm is introduced. In the other arm, oil of density 0.75 g/cm3 is poured till the upper surfaces of water and oil are at same horizontal level. Calculate the length of oilcolumn.
To solve the problem, we need to establish the relationship between the heights of the columns of water, oil, and mercury in the U-tube. Let's break it down step by step.
Step 1: Understand the Setup
We have a U-tube with mercury, water, and oil. The water column has a height of 8 cm, and the oil has a density of 0.75 g/cm³. The heights of the mercury in both arms of the U-tube will adjust until the pressure at the same horizontal level is equal.
Step 2: Establish the Pressure Balance
At the same horizontal level in both arms, the pressure exerted by the water column and the oil column plus the mercury column must be equal.
Let:
- y = height of the oil column
- x = height of the mercury column decrease in one arm (which will be the same in the other arm)
The pressure due to the water column can be expressed as:
Pwater=density of water×g×hwater=1g/cm3×9.8m/s2×8cm
Since we need to convert units, we can use g in cm/s² for simplicity:
Pwater=1×980dyne/cm2×8=7840dyne/cm2
Step 3: Write the Pressure Equation for Oil and Mercury
The pressure at the same height due to the oil and mercury can be expressed as:
Poil+Pmercury=density of oil×g×y+density of mercury×g×(2x)
Substituting the densities:
Poil=0.75g/cm3×980dyne/cm2×y
Pmercury=13.6g/cm3×980dyne/cm2×(2x)
Step 4: Set Up the Equation
Setting the pressures equal gives us:
7840=0.75×980×y+13.6×980×(2x)
Step 5: Relate x and y
From the geometry of the U-tube, we know:
2x+y=8cm(1)
From this equation, we can express y in terms of x:
y=8−2x(2)
Step 6: Substitute y into the Pressure Equation
Substituting equation (2) into the pressure equation:
7840=0.75×980×(8−2x)+13.6×980×(2x)
Step 7: Solve for x
Expanding and simplifying:
7840=735×(8−2x)+13.6×980×(2x)
Calculating the constants:
7840=5880−1470x+26.72×980x
Combine like terms and solve for x.
Step 8: Calculate y
Once you have x, substitute back into equation (2) to find y.
Final Calculation
After solving the above equations, you will find the length of the oil column y.
We have a U-tube with mercury, water, and oil. The water column has a height of 8 cm, and the oil has a density of 0.75 g/cm³. The heights of the mercury in both arms of the U-tube will adjust until the pressure at the same horizontal level is equal.
At the same horizontal level in both arms, the pressure exerted by the water column and the oil column plus the mercury column must be equal.
- y = height of the oil column
- x = height of the mercury column decrease in one arm (which will be the same in the other arm)
Pwater=density of water×g×hwater=1g/cm3×9.8m/s2×8cm
Since we need to convert units, we can use g in cm/s² for simplicity:
Pwater=1×980dyne/cm2×8=7840dyne/cm2
The pressure at the same height due to the oil and mercury can be expressed as:
Poil+Pmercury=density of oil×g×y+density of mercury×g×(2x)
Substituting the densities:
Poil=0.75g/cm3×980dyne/cm2×y
Pmercury=13.6g/cm3×980dyne/cm2×(2x)
Setting the pressures equal gives us:
7840=0.75×980×y+13.6×980×(2x)
From the geometry of the U-tube, we know:
2x+y=8cm(1)
From this equation, we can express y in terms of x:
y=8−2x(2)
Substituting equation (2) into the pressure equation:
7840=0.75×980×(8−2x)+13.6×980×(2x)
Expanding and simplifying:
7840=735×(8−2x)+13.6×980×(2x)
Calculating the constants:
7840=5880−1470x+26.72×980x
Combine like terms and solve for x.
Once you have x, substitute back into equation (2) to find y.
After solving the above equations, you will find the length of the oil column y.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (A. MCQ (Objectie Type Questions))
20 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (B. MCQ (AIPMT/NEET & Other State Boards For Medical Entrance))
6 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Long Answer Questions)
7 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
A vertical U tube of uniform cross section contains mercury in both of its arms. A glycerine (d=1.3g/cm3) column of length 10cm is introduced into one of the arms. Oil of density 0.8g/cm3 is poured in the other arm until the upper surfaces of the oil and glycerine are in the same horizontal level. Find the length of oil column. Densit of mercury is 13.6g/cm3.

View SolutionA vertical U-tube of uniform inner cross-section contains mercury in both of its arms. A glycerine (density1.3gcm−3) column of length 10cmis introduced into one of the arms Oil of density 0.8gcm−3 is poured in the other arm until the upper surface of the oil and glycerine are in the same horizontal level. Find the length of the oil column.
View Solution
Knowledge Check
An open U-tube contains mercury. When 11.2 cm of water is poured into one of the arms of the tube, how high does the mercury rise in the other arm from its initial level ?
A0.82 cmB1.35 cmC0.41 cmD2.32 cm
_S01_015_Q01.png)
A vertical U-tube of uniform cross-section contains mercury in both arms A glycerine (relative density =1.3) column of length 10 cm is introduced into one of the arms. Oil of density 800 gm m−3 is poured into the other arm until the upper surface of the oil and hlycerine are at the same horizontal level, find the length of the column. Density of mercury is 13.6×103kgm−3
View SolutionA vertical U-tube of uniform inner cross section contains mercury in both sides of its arms. A glycerin (density =1.3g/cm3) column of length 10 cm is introduced into one of its arms. Oil of density 0.8 gm/cm3 is poured into the other arm until the upper surfaces of the oil and glycerin are in the same horizontal level. Find the length of the same horizontal level. Find the length of the oil column, Density of mercury =13.6g/cm3
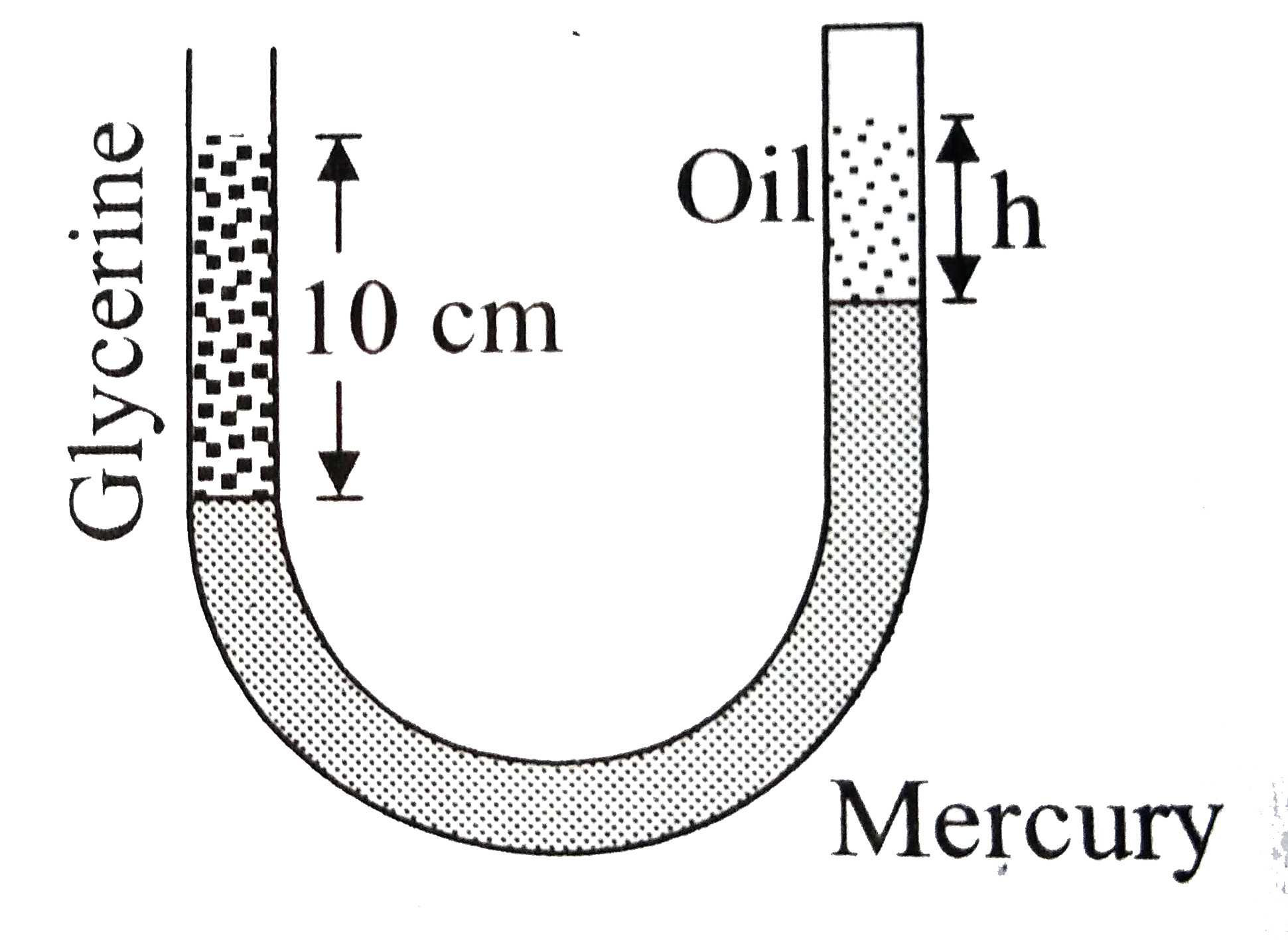
View SolutionA vertical U - tube of uniform cross - section contains water in both the arms. A 10 cm glycerine column (R.D. = 1.2) is added to one of the limbs. What is the level difference between the two free surface in the two limbs?
View SolutionA vertical U-tube of uniform cross-section contains water jn both the arms. A 10 cm glycerine column (R.D. = 1.2) is added to one of the limbs. The level difference between the two free surfaces in the two limbs wiil be
View SolutionA vertical U-tube of uniform cross-section contains water upto a height of 30 cm. show that if the water in one limb is depressed and then released, its up and down motion in the two limbs of the tube is simple harmonic and calculate its time-period.
View SolutionA vertical U-tube of uniform cross-section contains water upto a height of 30 cm. show that if the water in one limb is depressed and then released, its up and down motion in the two limbs of the tube is simple harmonic and calculate its time-period.
View SolutionA vertical U-tube of uniform cross-section contains water upto a height of 2.45 cm. show that if the water on one side is decpressed and then released, its up and down motion in the tube is SHM and calculate its time period. Given g=980cms−2.
View Solution
