The arranghement shown in the figure below consits of a block of mass 0.1 kg attached to a spring of force cosntant 2×10−3N/M with the help of a pulley so that the spring remians unstretched.On releasing the block , it starts oscillating with a small amplitude . The maximum velocity of block during this motion is close to
72m/s
71m/s
70m/s
69m/s
The correct Answer is:D
To solve the problem step by step, we will determine the maximum velocity of the block attached to the spring when it starts oscillating after being released.
Step 1: Identify the parameters
- Mass of the block, m=0.1kg
- Spring constant, k=2×10−3N/m
Step 2: Calculate the angular frequency ω
The angular frequency ω for a mass-spring system is given by the formula:
ω=√km
Substituting the values:
ω=√2×10−30.1=√0.02=0.1414rad/s
Step 3: Determine the amplitude A
When the block is released, it will stretch the spring until the spring force equals the gravitational force acting on the block. At maximum stretch (amplitude), we have:
kA=mg
Rearranging for A:
A=mgk
Substituting the known values:
A=0.1×9.82×10−3=0.980.002=490m
Step 4: Calculate the maximum velocity Vmax
The maximum velocity in simple harmonic motion is given by:
Vmax=ωA
Substituting the values of ω and A:
Vmax=0.1414×490≈69.3m/s
Conclusion
Thus, the maximum velocity of the block during its motion is approximately 69.3m/s.
- Mass of the block, m=0.1kg
- Spring constant, k=2×10−3N/m
The angular frequency ω for a mass-spring system is given by the formula:
ω=√km
Substituting the values:
ω=√2×10−30.1=√0.02=0.1414rad/s
When the block is released, it will stretch the spring until the spring force equals the gravitational force acting on the block. At maximum stretch (amplitude), we have:
kA=mg
Rearranging for A:
A=mgk
Substituting the known values:
A=0.1×9.82×10−3=0.980.002=490m
The maximum velocity in simple harmonic motion is given by:
Vmax=ωA
Substituting the values of ω and A:
Vmax=0.1414×490≈69.3m/s
Thus, the maximum velocity of the block during its motion is approximately 69.3m/s.
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice questions) AIPMT/NEET other State Boards for Medical Entrance
14 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition file (Multiple choice question) JEE (Main) & Other State Boards for Engineering Entrance
25 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Revision Exercises (Numerical Problems)
23 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
A block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionA block of mass 1 kg is suspended from a spring of constant 100 N/m. initially the spring is unstretched. The block is then released. What is the acceleration (in m/s2) of the block when its velocity is 0.6 m/s in the downwards direction ?
View Solution
Knowledge Check
a block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
A2⋅10−2JB2⋅10−6JC3⋅10−6JD4⋅10−2JA mass m=8kg is attached to a spring as shown in figure and held in position so that the spring remains unstretched. The spring constant is 200N/m. The mass m is then released and begins to undergo small oscillations. The maximum velocity of the mass will be (g=10m/s2)
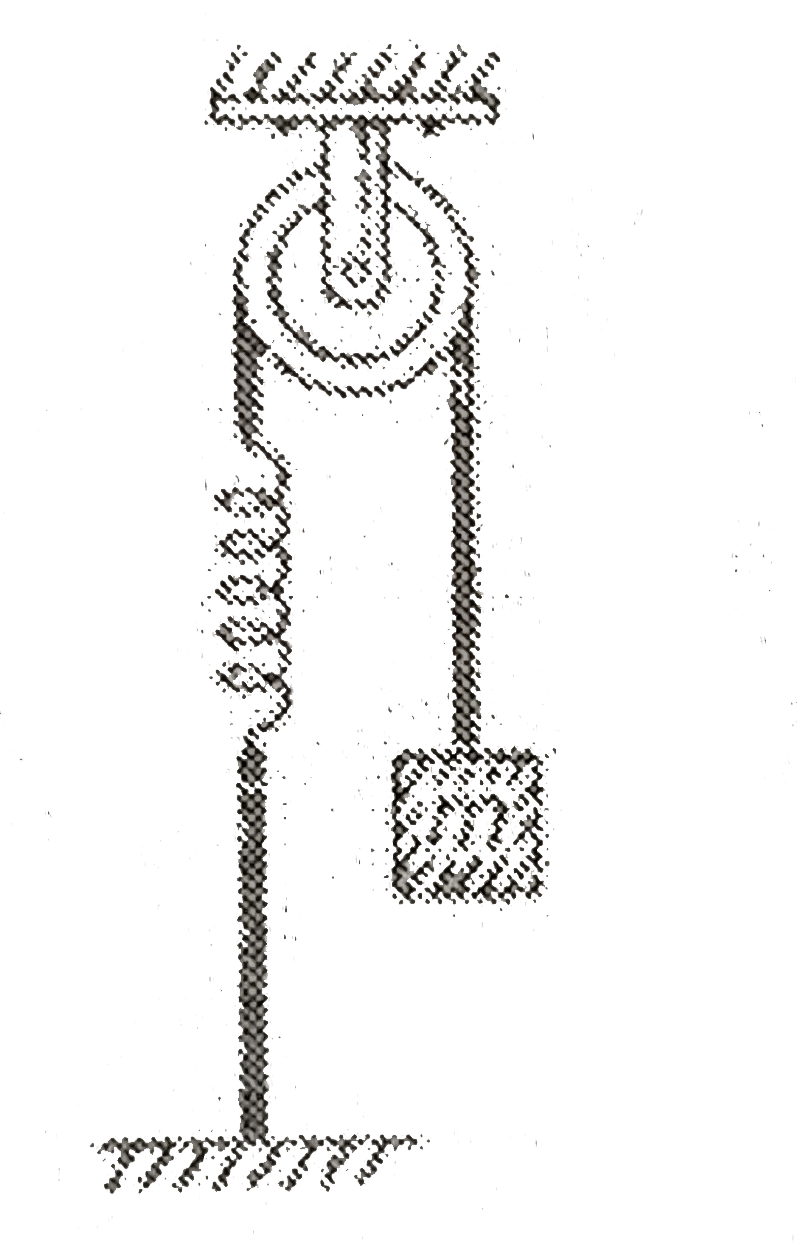 A1 m/sB2 m/sC4 m/sD5 m/s
A1 m/sB2 m/sC4 m/sD5 m/sIn the adjoining figure, block A is of mass (m) and block B is of mass2 m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched.
 .AThe maximum extension of the spring is 4mgk.BThe speed of A when extension in spring is 2mgk is 2g√2m3k.CThe acceleration of block B when the extension in the spring is maximum, is 23gDTension in the thread for extension of 2mgk in spring is mg
.AThe maximum extension of the spring is 4mgk.BThe speed of A when extension in spring is 2mgk is 2g√2m3k.CThe acceleration of block B when the extension in the spring is maximum, is 23gDTension in the thread for extension of 2mgk in spring is mg
A block of mass 100g attached to a spring ofstiffness 100N/Mis lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collation with the wall is elastic then find the time period of oscillations.

View SolutionA block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
View SolutionFigure shows two block A and B, each having a mass of 320 g connected by a light string passing over a smooth light pulley. The horizontal surface on which the block A can slide is smooth. The block A is attached to spring constant 40N/m whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take g=10m/s2 .
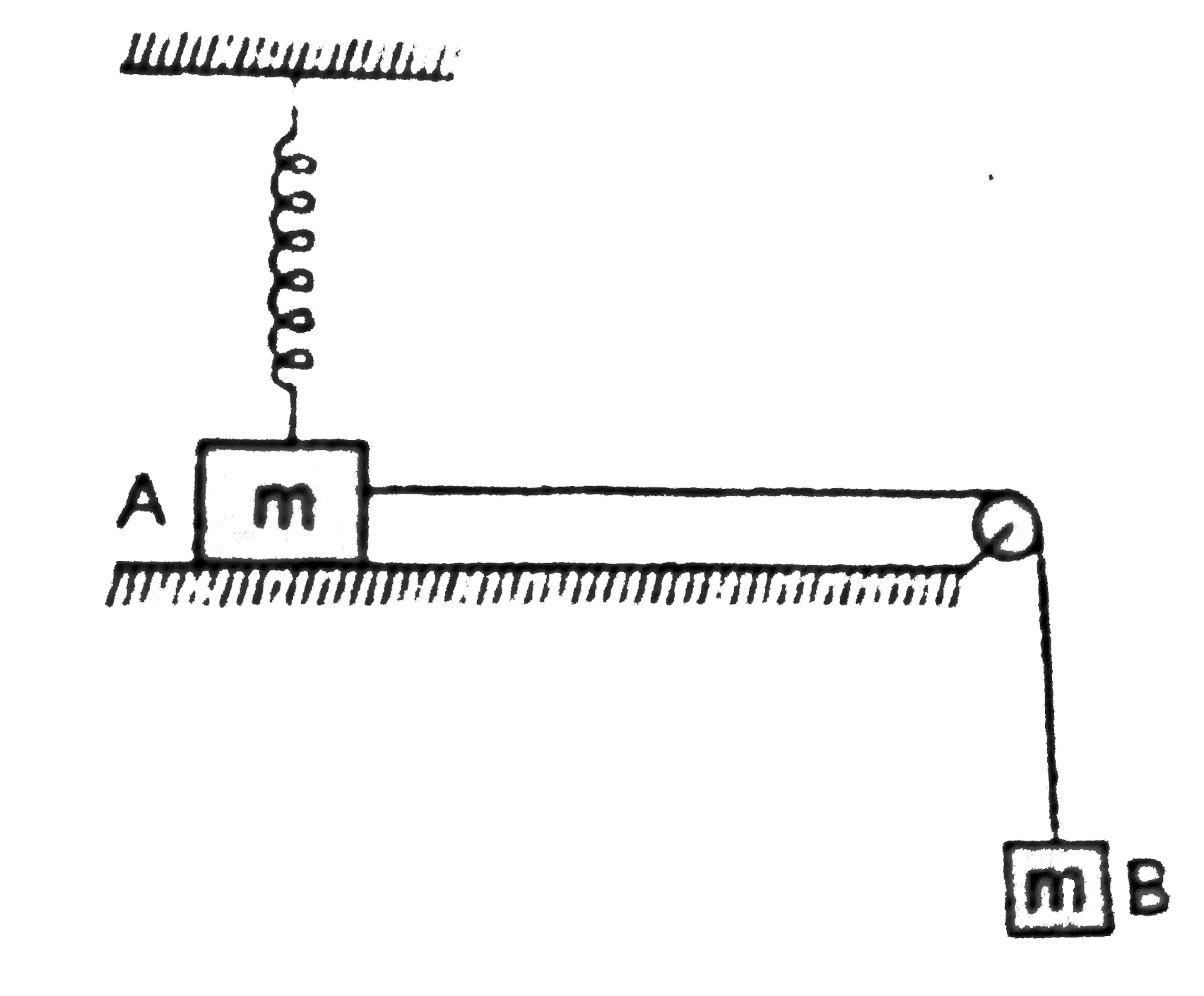
View SolutionA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
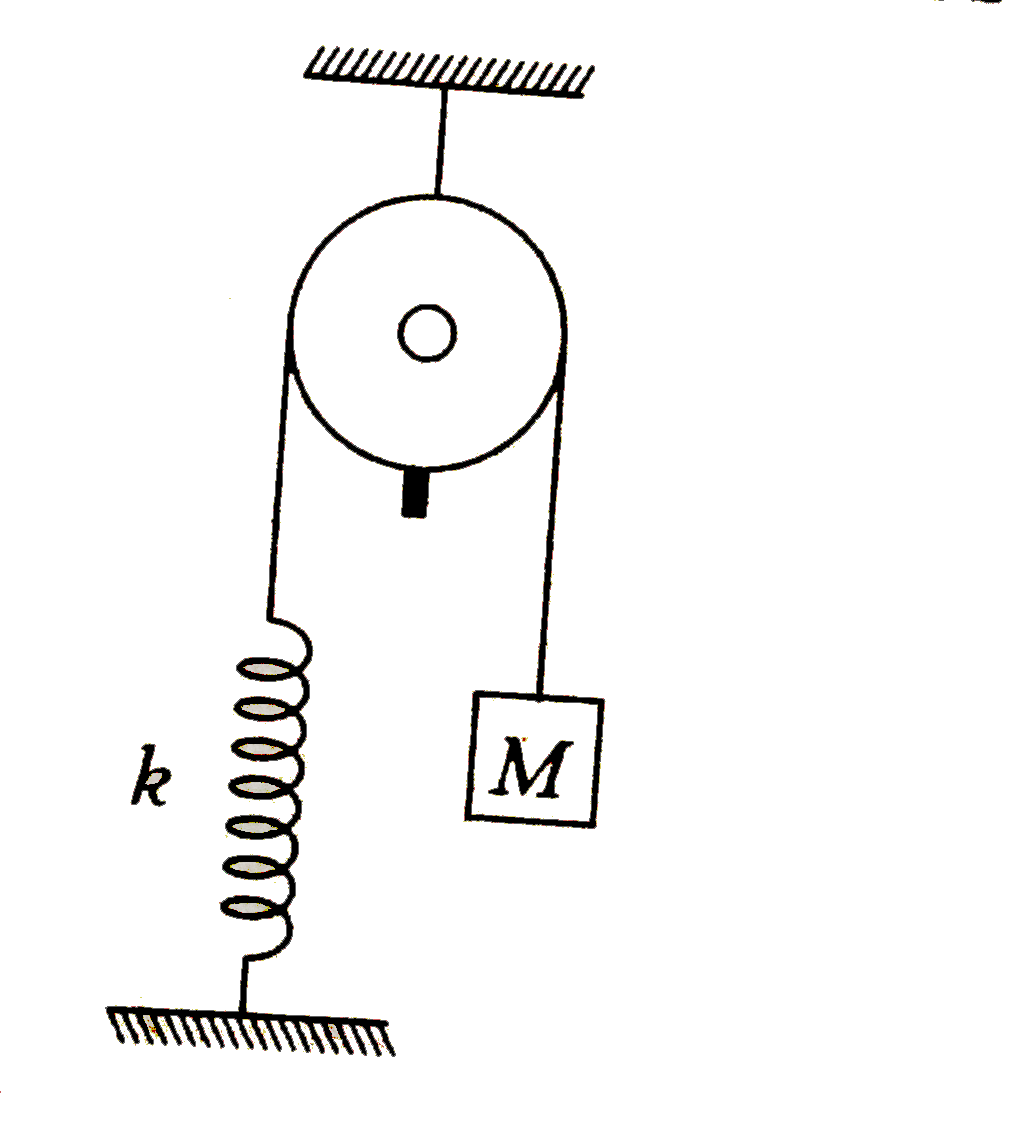
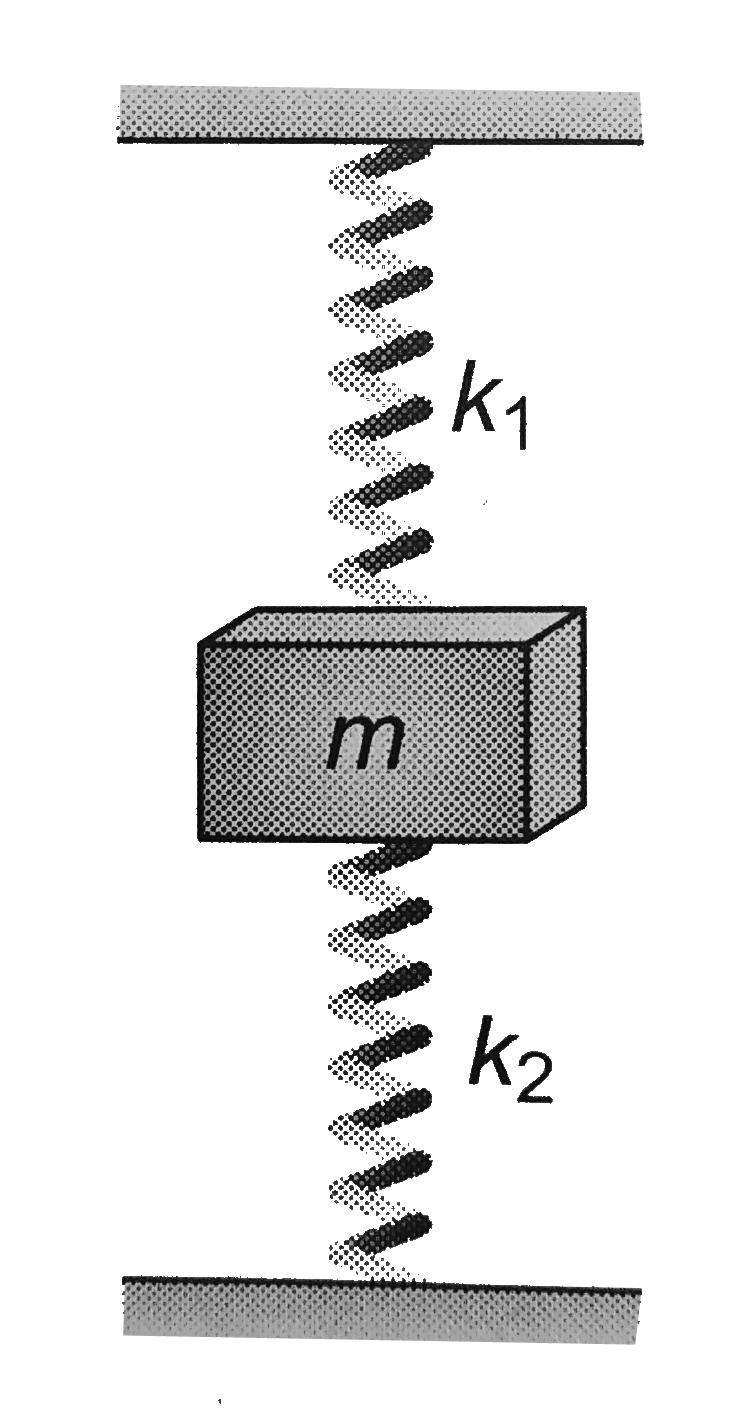
View SolutionIn the figure shown a block of masss m is atteched at ends of two spring The other ends of the spring are fixed The mass m is released in the vertical plane when the spring are released The velocity of the block is maximum when
View Solution