The atmosphere of earth extends upto height H and its refractive index varies with depth y from the top as μ=1+yH . Calculate the apparent thickness of the atmosphere as seen by an observer in space.
The correct Answer is:Hln2
To solve the problem of finding the apparent thickness of the Earth's atmosphere as seen by an observer in space, we can follow these steps:
Step 1: Understand the Refractive Index Variation
The refractive index μ of the atmosphere varies with depth y from the top as:
μ=1+yH
where H is the total height of the atmosphere.
Step 2: Set Up the Relationship for Apparent Thickness
The apparent thickness h′ of the atmosphere can be expressed in terms of the actual thickness dy and the refractive index μ:
dh′=dyμ
This means that the infinitesimal change in apparent thickness is the actual thickness divided by the refractive index.
Step 3: Substitute the Expression for μ
Substituting the expression for μ into the equation gives:
dh′=dy1+yH
Step 4: Simplify the Expression
We can rewrite the equation as:
dh′=dyH+yH=HdyH+y
Step 5: Integrate to Find Total Apparent Thickness
To find the total apparent thickness h′, we need to integrate dh′ from y=0 to y=H:
h′=∫H0HdyH+y
Step 6: Perform the Integration
The integral can be computed as follows:
h′=H∫H0dyH+y
This integral can be solved using the natural logarithm:
∫dyH+y=ln(H+y)
Thus, evaluating the limits:
h′=H(ln(H+y))H0=H(ln(2H)−ln(H))=Hln(2)
Final Result
The apparent thickness of the atmosphere as seen by an observer in space is:
h′=Hln(2)
---
The refractive index μ of the atmosphere varies with depth y from the top as:
μ=1+yH
where H is the total height of the atmosphere.
The apparent thickness h′ of the atmosphere can be expressed in terms of the actual thickness dy and the refractive index μ:
dh′=dyμ
This means that the infinitesimal change in apparent thickness is the actual thickness divided by the refractive index.
Substituting the expression for μ into the equation gives:
dh′=dy1+yH
We can rewrite the equation as:
dh′=dyH+yH=HdyH+y
To find the total apparent thickness h′, we need to integrate dh′ from y=0 to y=H:
h′=∫H0HdyH+y
The integral can be computed as follows:
h′=H∫H0dyH+y
This integral can be solved using the natural logarithm:
∫dyH+y=ln(H+y)
Thus, evaluating the limits:
h′=H(ln(H+y))H0=H(ln(2H)−ln(H))=Hln(2)
The apparent thickness of the atmosphere as seen by an observer in space is:
h′=Hln(2)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 2
62 Videos
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 3
9 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- MAGNETIC EFFECT OF CURRENTBOOK - ARIHANTCHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - Magnetic effect of Current
45 Videos
Similar Questions
Apparent velocity of fish floating in tank
A tank is filled with water up to a height of 15cm and a fish is floating inside at a depth of 10cm. The tank is now being drained so that the surface moves down with a velocity of 1cm/s. An observer is viewing the fish from a height of 10cm.
(a) Find the apparent velocity of the fish as seen by the observer.
Find the apparent velocity of the observer as seen by the fish.
View SolutionAtmosphere of a planet contains only an ideal gas of molar mass M0. The temperature of the atmosphere varies with height such that the density of atmosphere remains same throughout. The planet is a uniform sphere of mass M and radius ‘a’. Thickness of atmosphere is small compared to ‘a’ so that acceleration due to gravity can be assumed to be uniform throughout the atmosphere.
(a) Find the temperature difference between the surface of the planet and a point at height H in its atmosphere
(b) If the rms speed of gas molecules near the surface of the planet is half the escape speed, calculate the temperature of the atmosphere at a height H above the surface. Assume CpCV=γ for the atmospheric gas
View Solution
Knowledge Check
A bird in air looks at a fish vertically below it and inside water. h1 is the height of the bird above the surface of water and h2, the depth of the fish below the surface of water. If refractive index of water with respect to air be μ, then the distance of the fish as observed by the bird is
Ah1+h2Bh1+h2μCμh1+h2Dμh1+μh2A beaker contains water up to a height h1 and kerosene of height h2 above water so that the total height of (water + kerosene) is (h1+h2) . Refractive index of water is μ1 and that of kerosene is μ2 . The apparent shift in the position of the bottom of the beaker when viewed from above is :-
A(1−1μ1)h2B(1−1μ1)h1+(1−1μ2)h2C(1−1μ1)h1D(1+1μ1)h2−(1+1μ2)h1A cylinder is filled with a liquid of refractive index μ. The radius of the cylinder is decreasing at a constant rate K. The volume of the liquid inside the container remains constant at V. The observer and the object O are in a state of rest at a distance L from each other. When radius of cylinder is r the apparent velocity of the object as seen by the observer is
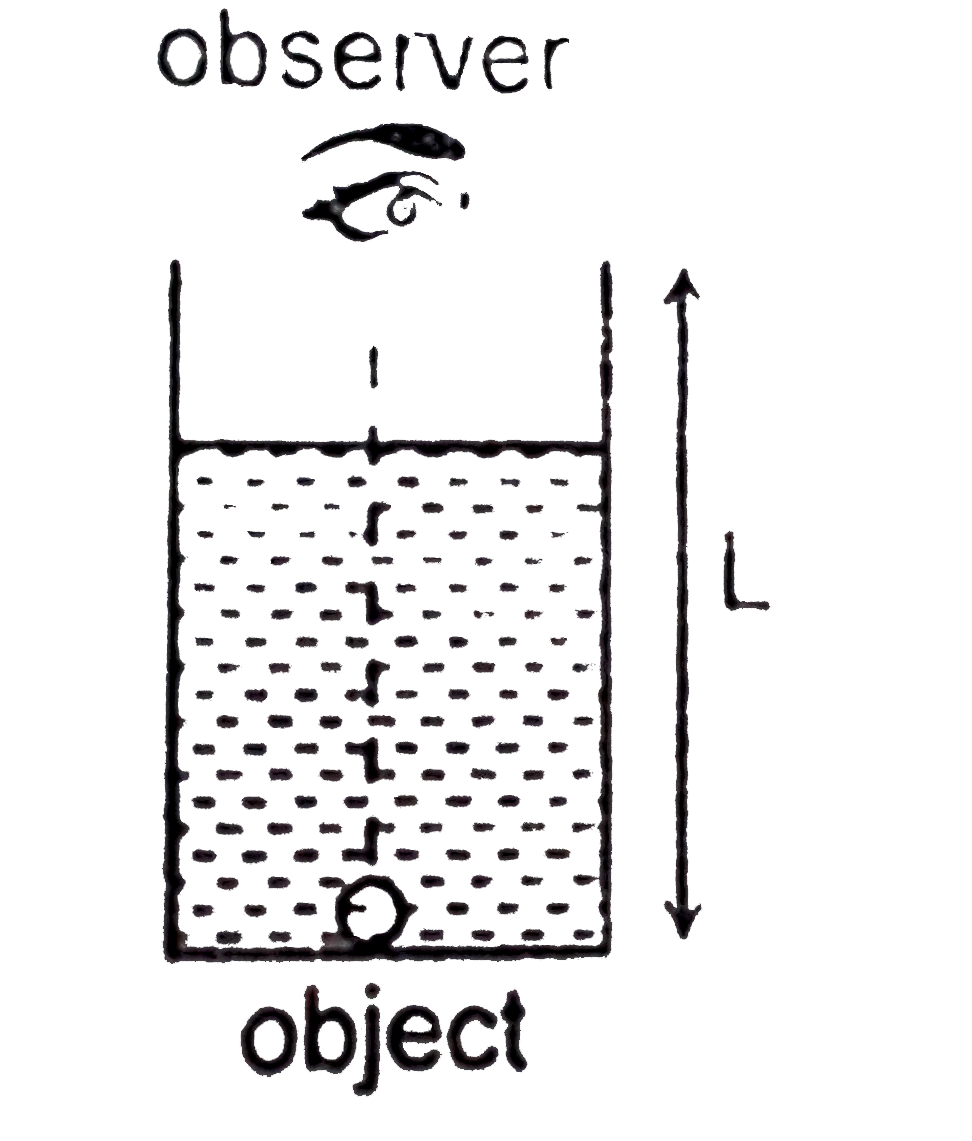 A(1−μ)2KV(πμr3)B(1−μ)2KV(πμlr2)C(1−μ)2KμD(1−μ)K2μ
A(1−μ)2KV(πμr3)B(1−μ)2KV(πμlr2)C(1−μ)2KμD(1−μ)K2μ
A glass slab is placed between an object (O) and an observer (E) with its refracting surfaces AB and CD perpendicular to the line OE. The refractive index of the glass slab changes with distance (y) from the face AB as μ=μ0(1+y). Thickness of the slab is t. Find how much closer (compared to original distance) the object appears to the observer. Consider near normal incidence only.
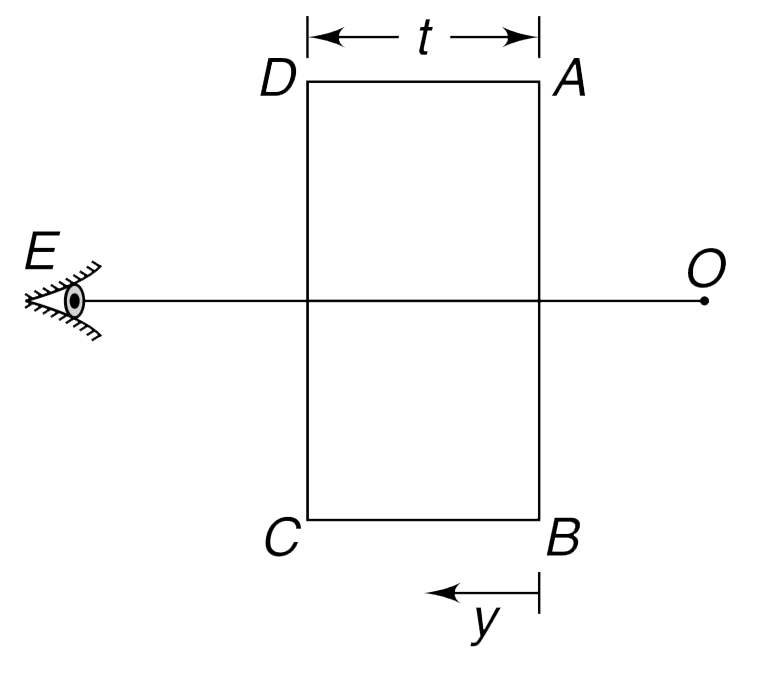
View SolutionA point object O is placed in fornt of a transparent slab at a distance x from its surface. It is seenfrom the other side of he slab by light incident nearlyl normally to the slab. The thickness of the slab is t and its refractive index is μ. Show that the apparent shift in the position of the object is independent of x and find its value.
View SolutionA plane mirror is fixed at the bottom of a vessel as shown in the figure. Water of refractive index μ is filled up to a height h in the vessel. There is a fish at a height h/2 from bottom of vessel and there is a bird at a height h above the surface of water in the vessel.
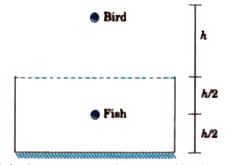
(a) Calculate apparent distance of bird as seen by the fish.
(b) Calculate apparent distance of image of bird in mirror as seen by the fish.
(c) Calculate apparent distance of fish as seen by the bird.
(d) Calculate apparent distance of image of fish in the mirror as seen by the bird.
View SolutionA vessel of depth 2d is half filled with a liquid of refractive index n1 and the upper half with a liquid of refractive index n2. The apparent depth of the vessel when seen normally from the top is
View SolutionA vessel of depth 2d cm is half filled with a liquid of refractive index μ1 and the upper half with a liquid of refractive index μ2. The apparent depth of the vessel seen perpendicularly is
View Solution
