The basket in a front loading automatic clothes dryer rotates about a horizontal axis. The basket rotates so that the force exerted by the basket on clothes located at the basket's edge is zero at the top of the path. If the radius of the basket is 0.65 m, how fast must the basket turn to accomplish this ?
The correct Answer is:B, C
Step by step video, text & image solution for The basket in a front loading automatic clothes dryer rotates about a horizontal axis. The basket rotates so that the force exerted by the basket on clothes located at the basket's edge is zero at the top of the path. If the radius of the basket is 0.65 m, how fast must the basket turn to accomplish this ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - MCQ
158 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
An automatic tumble dryer has a 0.65 m diameter basket that rotates about a horizontal axis. As the basket turns, the clothes fall away from the basket at a point 60∘ from the vertical what is the rate of rotation of dryer drum ? Take g=10m/s2
View SolutionA horizontal disc of radius R rotates with a constant angular velocity ω about a stationary vertical axis passing through its edge. Along the circumference of the disc a particle of mass m moves with a velocity that is constant relative to the disc. At the moment when the particle is at the maximum distance from the rotation axis, the resultant of the inertial forces Fin acting on the particle in the reference frame fixed to the disc turns into zero. Find:
(a) the acceleration w′ of the particle relative to the disc,
(b) the dependence of Fin on the distance from the rotation axis.
View Solution
Knowledge Check
Components of loudspeaker :
A loudspeaker consists of permanent magnets, basket, voice cails, flexible supension & rigid speaker cone as shown in figure.
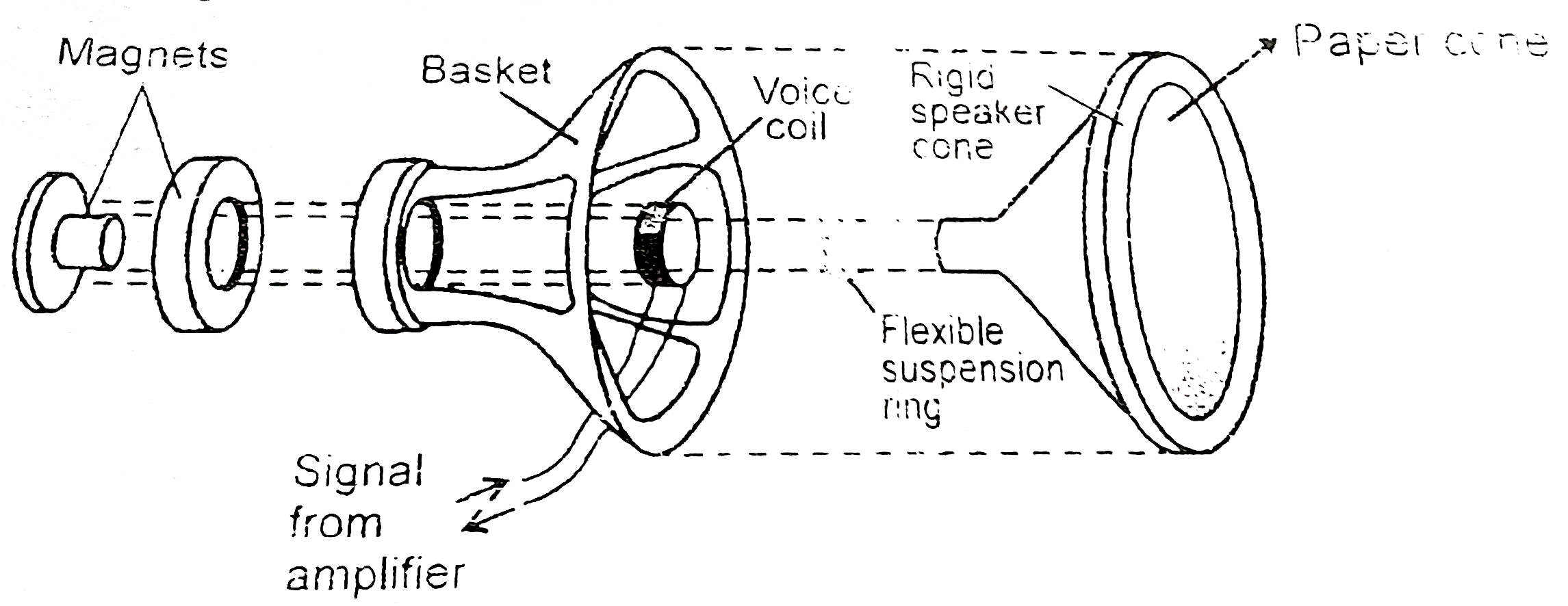
Loudspeaker principle
A light voice coil is mounted so that it can move freely inside the magnetic field of a strong permanent magnet. the paper cone is attached to the voice coil and attached with a flexble mounting to the outer ring of the support .Because there is a definite equilibrium position for the speaker cone and there is elasticity of the mounting structure, there is inevitably a free cone resonant frequency like of a mass on a spring. The frequency can be determined by adjusting the mass and stiffness of the cone and voice coil
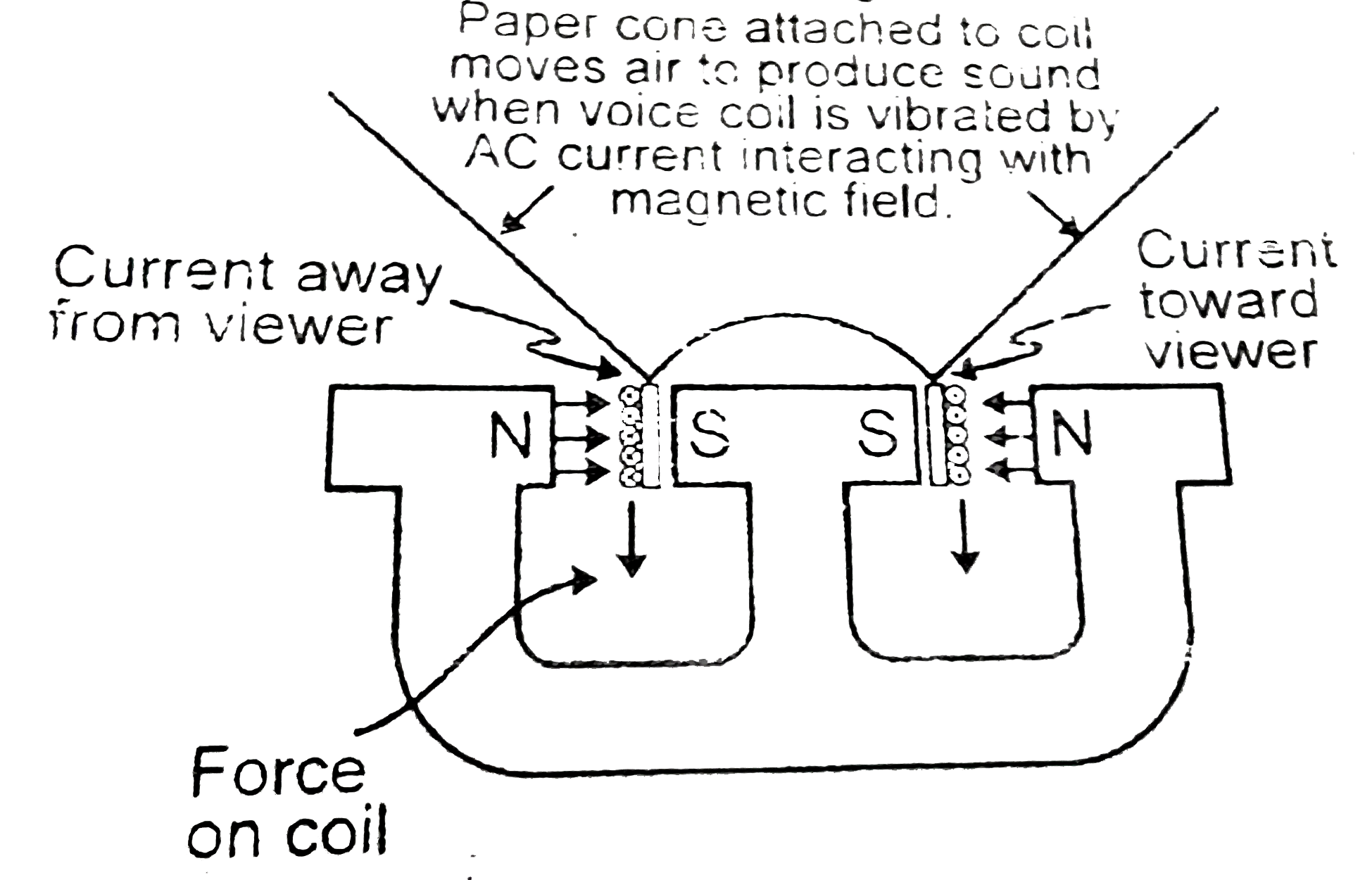
Working :
The ratio drives a rapidly changing current through the coil. The current follows that vibrations of speech and the electromagnetic force follows the current changes, pushing the paper cone. Finally the air in front of the loudspeaker is set into vibration following the cone's motion, and sound waves are transmitted to the listener
If the diameter of the cylindrical magnet, number of turns of the coil and cross-section area of the wire of the coil are all doubled, then the magentic force on the coil assuming the same potential difference , is (assume that value of magnetic field also gets doubled)AsameBdoubledCbecomes 8 timesDbecomes four timesMarket day in a village is enjoyed by children and women and men. It is a good place for farmers to sell their vegetables and grain and all the things they grow in their fields. Early in the morning, the farmers load their bullock carts and tractors with sacks full of grain and baskets full of fruits and vegetables. They also carry their sheep and goats, cows and buffaloes and chickens that they want to sell at the market. They need to buy things also at the market. They need clothes and spices, and also several household goods. These things are not easily available near their farms.
The women buy colourful glass bangles from the bangle sellers. Fires are lit. Pakoras, puris and sabzi are cooked. Samosas and sugarcane juice are also very popular. Children run around happily with their friends. They take rides on swings and merry- go-rounds. Everyone loves a market day.
How do the farmers carry their vegetables and grains to the market?Ain their trucks and carsBin their bullock carts and tractorsCThe farmers themselves carry them ontheir heads.DThey are carried by helpers and friendsA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The net work done by forces exerted by the disc on the ball for the duration ball remains on the disc isA2mR2ω209BmR2ω2018CmR2ω206DmR2ω209
A man of mass m1 stands on the edge of a horizontal uniform disc of mass m2 and radius R which is capable of rotating freely about a stationary vertical axis passing through its centre. At a certain moment the man starts moving along the edge of the disc, he shifts over an angle φ′ relative to the disc and then stops. In the process of motion the velocity of the man varies with time as v′(t).
Assuming the dimensions of the man to be negligible, find:
(a) the angle through which the disc had turned by the moment the man stopped,
(b) the force moment (relative to the rotation axis) with which the man acted on the disc in the process of motion.
View SolutionA thread is tightly wrapped on two pulleys as shown in figure. Both the pulleys are uniform disc with upper one having mass M and radius R being free to rotate about its central horizontal axis. The lower pulley has mass m and radius r and it is released from rest. It spins and falls down. At the instant of release a small mark (A) was at the top point of the lower pulley.
(a) After what minimum time (t0) the mark will again be at the top of the lower pulley?
(b) Find acceleration of the mark at time t0.
(c) Is there any difference in magnitude of acceleration of the mark and that of a point located on the circumference at diametrically opposite end of the pulley.
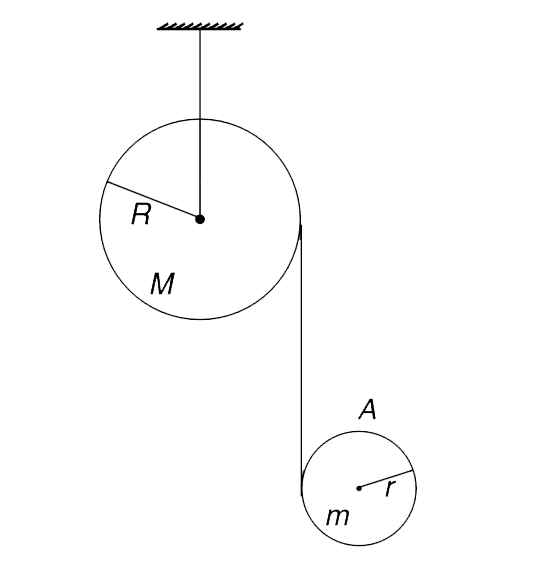
View SolutionA hot- air balloon consists of a basket, one passenger, and some carge. Let the total mass be M. Even though there is an upward lift force on the balloon, the balloon is initially acceleration downwards at a rate of g/3.
(a) Draw a free-body diagram for the descending balloon.
(b) Find the upward lift force in terms of the initial total weight Mg.
(c ) The passenger notices that he is heading straight for a waterfall and decides he needs to go up. What fraction of the total weight must he drop overboard so that the balloon accelerates upward at a rate of g/2? Assume that the upward lift force remains the same.
View SolutionA horizontally oriented uniform rod AB of mass m=1.40kg and length l0=100cm rotates freely about a stationary vertical axis OO′ passing through its end A. The point A is located at the middle of the axis OO′ whose length is equal to l=55cm. At what angular velocity of the rod the horizontal component of the force acting on the lower end of the axis OO′ is equal to zero? What is in this case the horizontal component of the force acting on the upper end of the axis?
View SolutionA horizontally oriented uniform disc of mass M and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass m. A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with ann angular velocity ω0. Then by means of a force F applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
(b). The work performed by the force F.
View Solution
