A thread is tightly wrapped on two pulleys as shown in figure. Both the pulleys are uniform disc with upper one having mass M and radius R being free to rotate about its central horizontal axis. The lower pulley has mass m and radius r and it is released from rest. It spins and falls down. At the instant of release a small mark (A) was at the top point of the lower pulley.
(a) After what minimum time (t0) the mark will again be at the top of the lower pulley?
(b) Find acceleration of the mark at time t0.
(c) Is there any difference in magnitude of acceleration of the mark and that of a point located on the circumference at diametrically opposite end of the pulley.
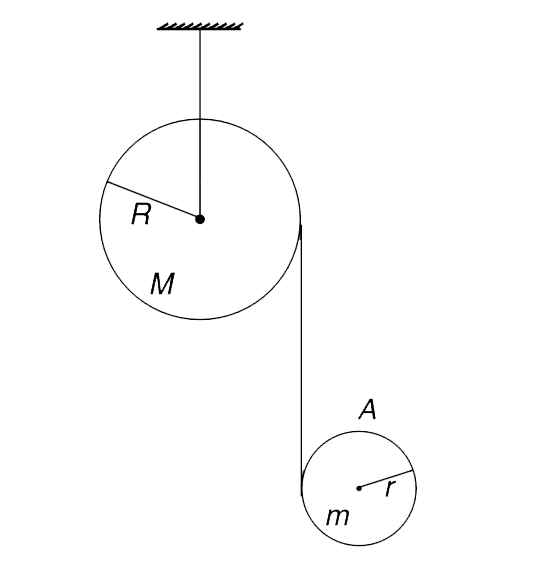
The correct Answer is:(a) t0=√2π(2m+3M)rMg
(b) a=2g2m+3Mn√m2+(4πM+M+m)2
(c) yes
Topper's Solved these Questions
Similar Questions
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View Solution-
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View Solution
Knowledge Check
A uniform disc of mass M and radius R is pivoted about a horizontal axis passing through its edge. It is released from rest with its centre of mass at the same height as the pivot.
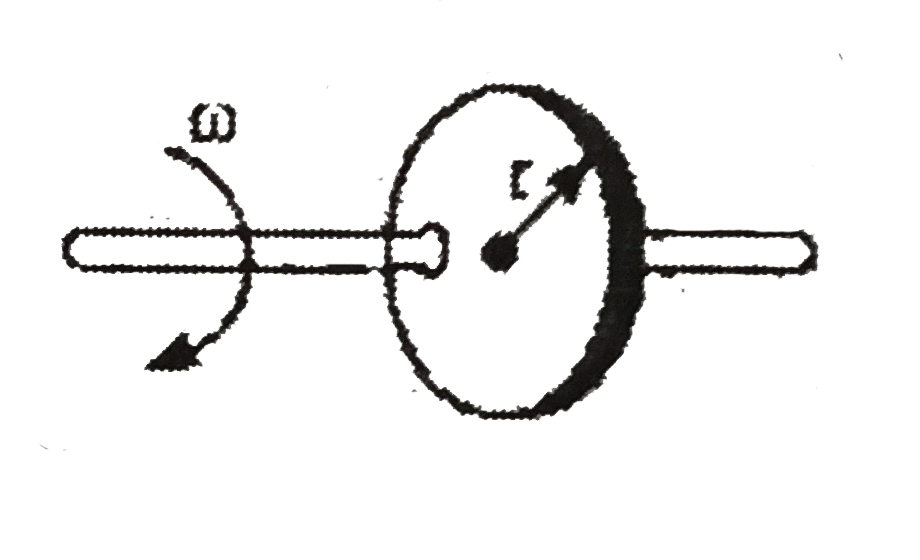AThe angular velocity of disc when its centre of mass is directly below the pivot is √4g3rBThe force exerted by the pivot at this instant is 73mgCAngular momentum of disc is conservedDAngular acceleration of disc at the given instant is zeroIn the arrangement shown in figure two equal masses (each m) hung light cords wrapped around a uniform solid cylinder of mass M and radius R. The cylinder is free to roate about a harizontal axis. If the system is released from rest then, the tension in each cord is-
AMmg4m+MBMmgm+MCMmgM+3mDMmg2m+MA uniform solid cylinder of mass M and of radius R rotates about a frictionless axle. Two masses are suspended from a rope wrapped arround the cylinder. If the system is released from rest, the tension in each rope is?
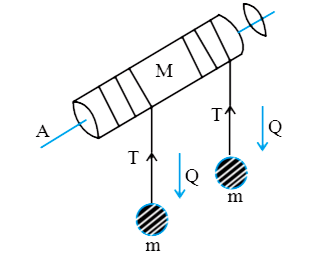AMmgM+mBMmgM+2mCMmgM+3mDMmgM+4m
A uniform solid cylinder of mass M and of radius R rotates about a frictionless axle. Two masses are suspended from a rope wrapped arround the cylinder. If the system is released from rest, the tension in each rope is?
View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View SolutionA frictionless pulley has the shape of a uniform solid disc of mass M and radius R. A stone of mass m is attached to a light wire that is wrapped around the rim of the pulley and a system is released from rest. If a stone falls by a distance h, what is the angular speed of pulley at that moment?
View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-
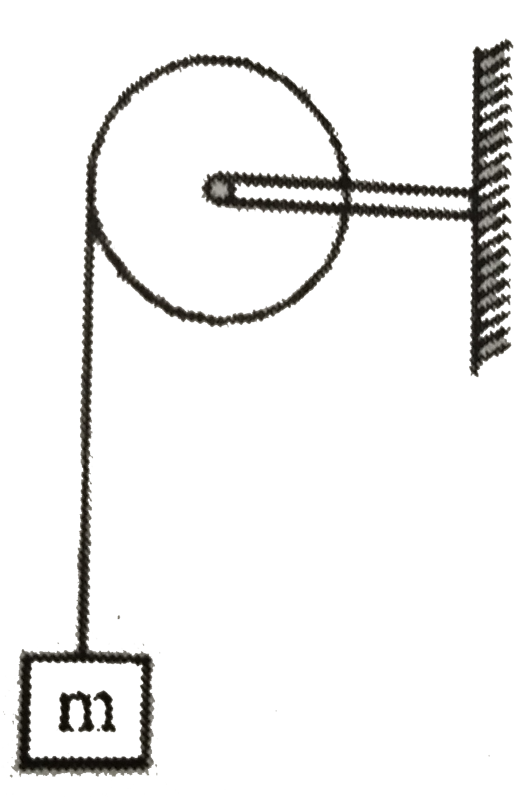
View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View Solution