The block in Fig. 8-12a lies on a horizontal frictionless surface, and the spring constant is 50 N/m. Initially, the spring is at its relaxed length and the block is stationary at position . Then an applied force with a constant magnitude of 3.0 N pulls the block in the positive direction of the axis, stretching the spring until the block stops. When that stopping point is reached, what are (a) the position of the block, (b) the work that has been done on the block by the spring force ? During the block's displacement, what are (d) the block's position when its kinetic energy is maximum and (e) the value of that maximum kinetic energy ?
The correct Answer is:(a) 0.12 m ; (b) 0.36 J ; (c) - 0.36J; (d) 0.060 m; (e) 0.090 J
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:PRACTICE QUESTIONS (Single Correct Choice Type)
Explore 59 Videos
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:PRACTICE QUESTIONS (More than one choice correct type)
Explore 10 Videos
- WORK, POWER, AND ENERGYBook:RESNICK AND HALLIDAYChapter:WORK, POWER, AND ENERGYExercise:CHECKPOINT
Explore 6 Videos
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Practice Questions (Integer Type)
Explore 4 Videos
Similar Questions
A block of mass m lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant k) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched (x=0). When a constant horizontal force →F in the positive direction of the x−axis is applied to it, a plot of the resulting kinetic energy of the block versus its position x is shown in figure. What is the magnitude of →F ?
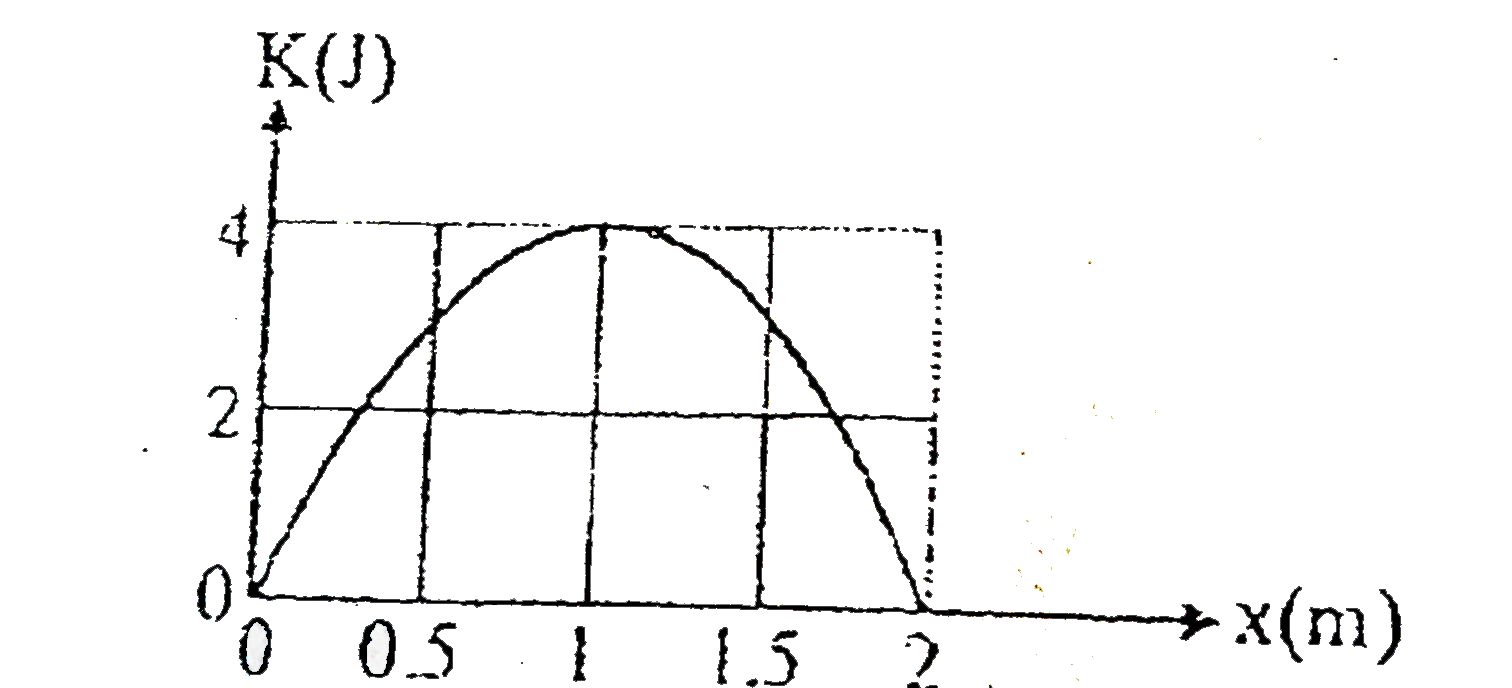
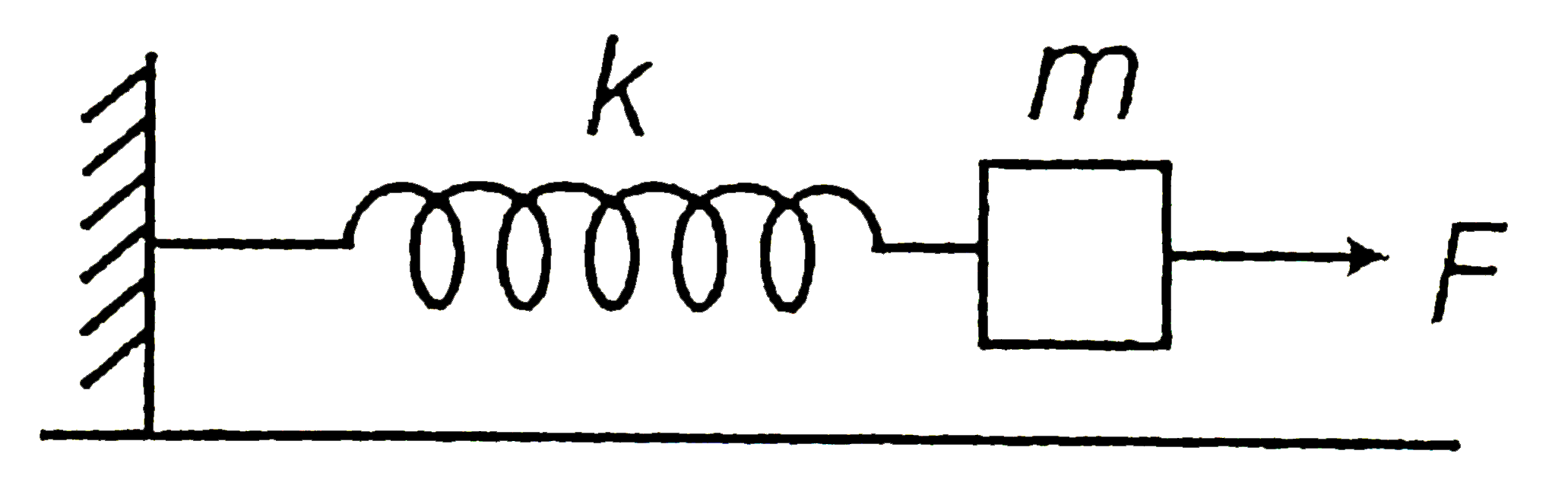
View SolutionThe figure showns a mass m on frictionless surface It is connected to righd wall by the mean of a massless spring of its constant K. Initially , The spring at its natural position.If a force of constant magnitude starts actiing on the block towareds right, then the speed of the block when the defromation in spring is x, will be
View Solution
Knowledge Check
A block of mass m lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant k) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched (x=0). When a constant horizontal force →F in the positive direction of the x−axis is applied to it, a plot of the resulting kinetic energy of the block versus its position x is shown in figure. What is the magnitude of →F ?
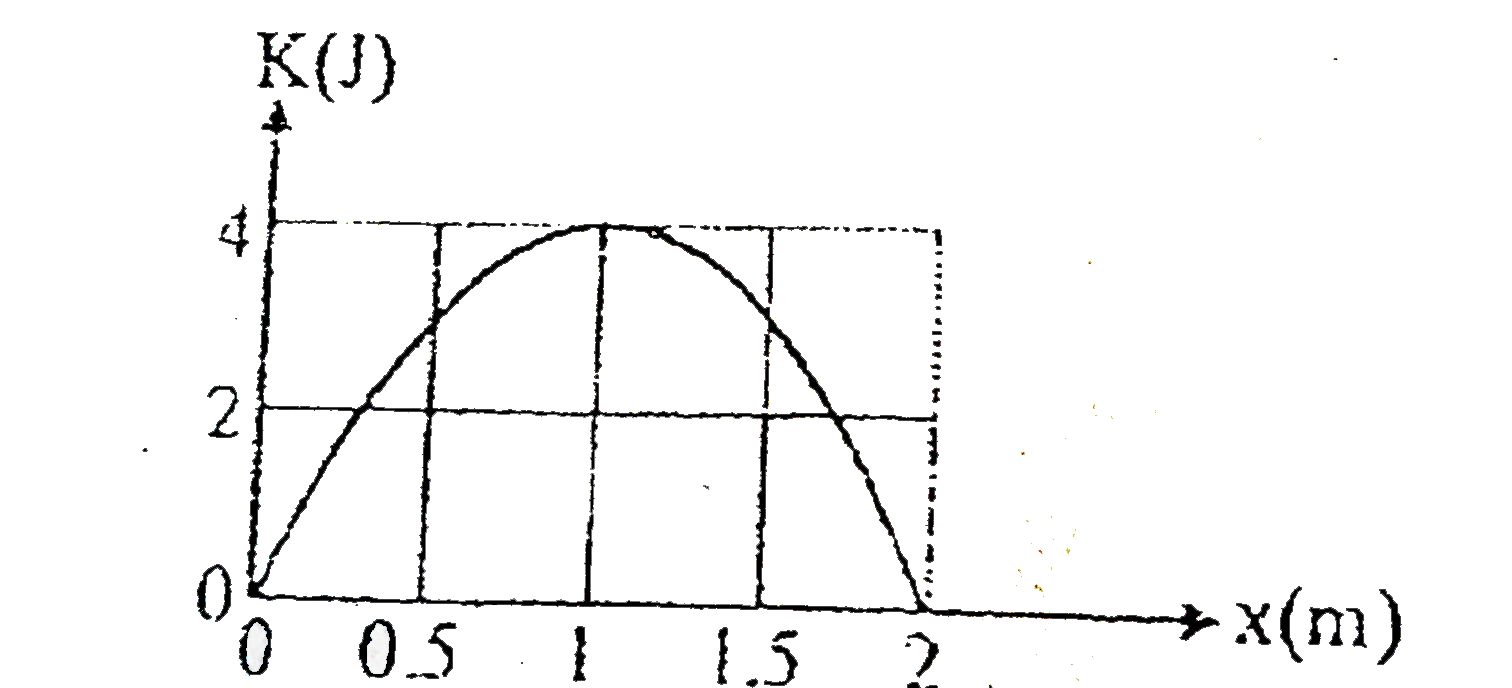 A2NB4NC8ND16N
A2NB4NC8ND16NA block of mass m lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant k) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched (x=0). When a costant horizontal force →F in the positive direction of the x−axis is applied to it, a plot of the resulting kinetic energy of the block verus its position x is shown in figure. What is the magnitude of →F
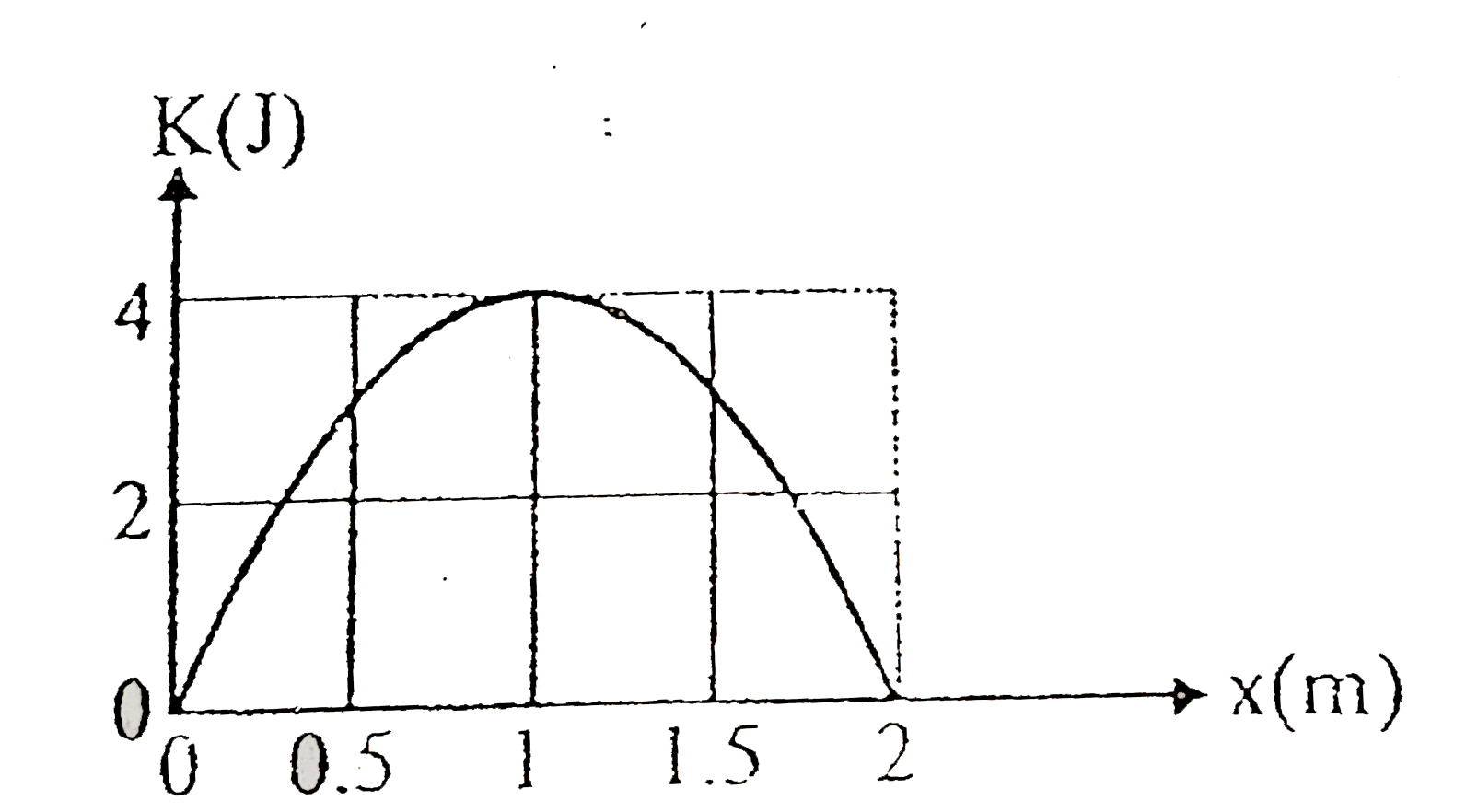 A2NB4NC8ND16N
A2NB4NC8ND16NTwo blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
AF=μ(m1+m22)gBF=μ(m12+m2)gCF=μ(m21+m222)gDF=μ2(m21+m22)g
A block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is

View SolutionA block of mass m=2kg is connected to a a spring of force constant k=50N/m. Initially the block is at rest and tlhe spring has natural length. A constant force F=60N is applied horizontally towards, the maximum speed of the block (in m/s) will be (negelect friction).

View SolutionA block of mass m=2kg is connected to a a spring of force constant k=50N/m. Initially the block is at rest and tlhe spring has natural length. A constant force F=60N is applied horizontally towards, the maximum speed of the block (in m/s) will be (negelect friction).

View SolutionThe figure shown a mass m on frictionless surface It is connected to rigid wall by the mean of a massless spring of its constant K. Initially , The spring at its natural position. If a force of constant magnitude starts acting on the block towards right, then the speed of the block when the deformation in spring is x, will be

View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is

View Solution
