The block on the loop shown slides without friction. At what height from A it starts so that it passes against the track at B with a net upward force equal to its own weight? The radius of the loop is R.
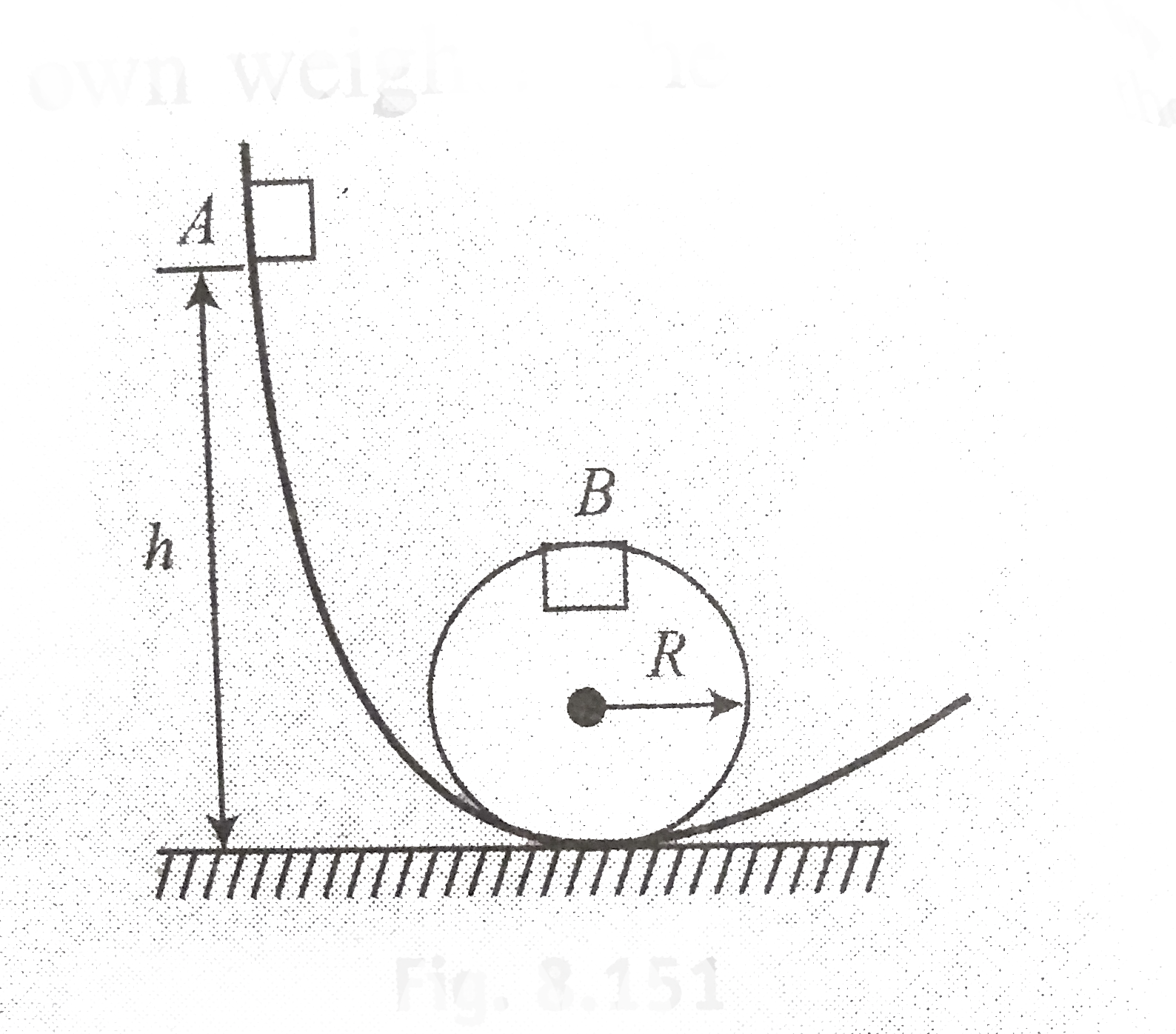
The correct Answer is:C
Step by step video, text & image solution for The block on the loop shown slides without friction. At what height from A it starts so that it passes against the track at B with a net upward force equal to its own weight? The radius of the loop is R. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - MCQ
158 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
A small block of mass m slides along a smooth frictional track as shown in the figure. If it starts from rest at P, what is the resultant force acting on it at Q?

View SolutionIn the figure of problem 17 if the block starts from rest when R=5r, what is the reaction of the inner track on the sliding mass at the highest point ? From what height should it fall so that it may exert a force equal to its weight on the track at the highesth point ?
View Solution
Knowledge Check
An object of mass m is released from rest at a height h above the surface of a table. The object slides along the inside of the loop. The loop track consisting of a ramp and a circular loop of radius R shown in the figure. Assume that the track is frictionless. When the object is at the top of the circular track it pushes against the track with a force equal to three times its weight. What height was the object dropped from?
 A3RB4RC5RD6R
A3RB4RC5RD6RA mass m starting from A reaches B of a frictionless track. On reaching B, it pushes the track with a force equal to x times its weight, then the applicable relation is
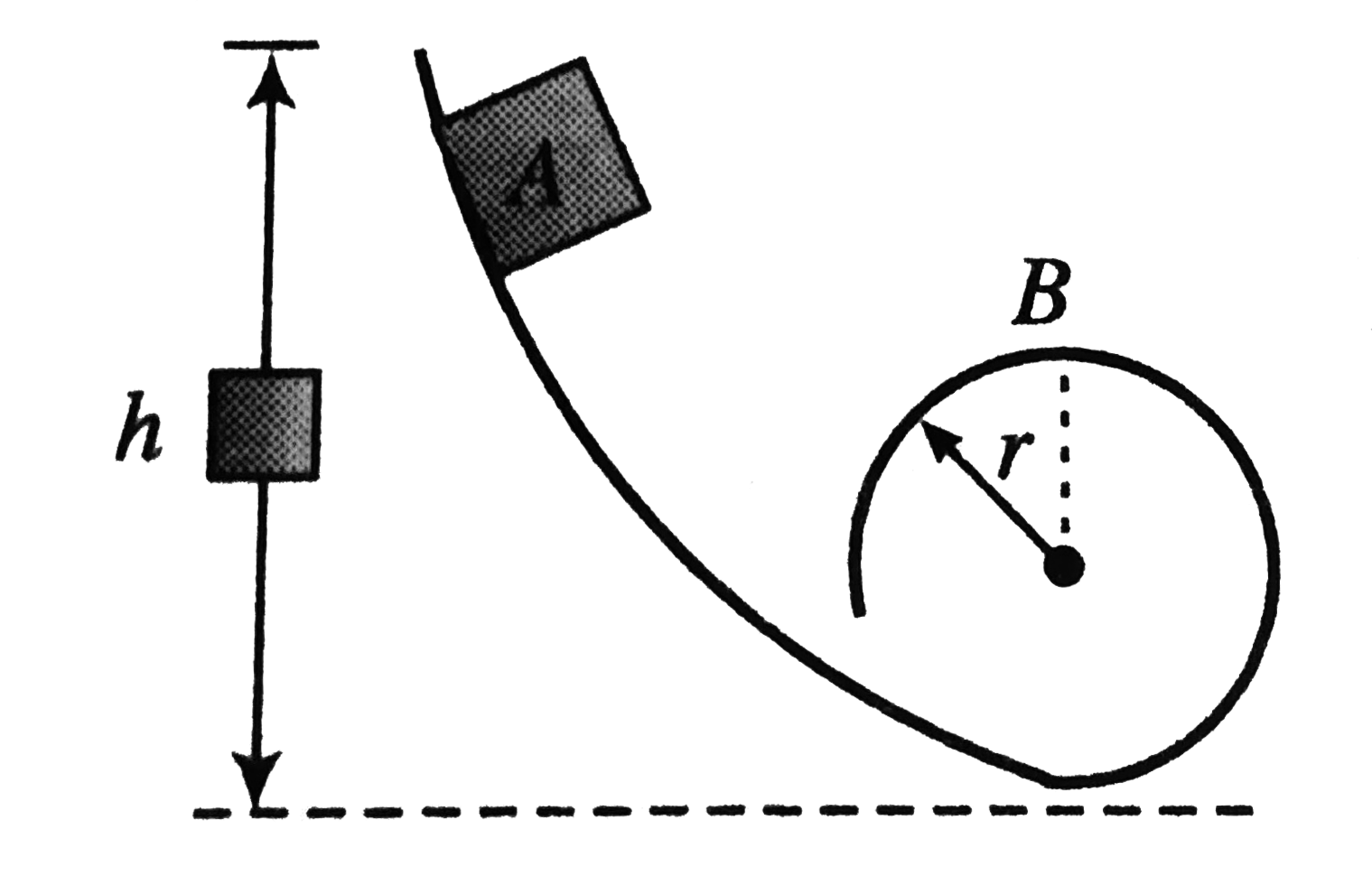 A(a) h=(x+5)2rB(b) h=x2rC(c) h=rD(d) h=(x+12)r
A(a) h=(x+5)2rB(b) h=x2rC(c) h=rD(d) h=(x+12)r
Figure shows a smooth track, a part of which is a circle of radius r. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.

View SolutionA small block of mass m slides along a smooth frictionless track as shown.
(a) If it starts from rest at P, what is the resultant force acting on it at Q?
(b) At what height above the bottom should the block be released so that the force it exerts against the track at the top of the loop equals its weight?

View SolutionA small body of mass m slides without friction from the top of a hemisphere of radius r. At what hight will the body be detached from the centre of hemisphere?

View SolutionA small block of mass m slides along a smooth track, as shown in fig. (i) If it starts from rest at P, what is the resulting force acting on it at Q ? (ii) at what height above the bottom of the loop should the block be released so that the force it exerts against the track at the top of the loop equals its weight?

View SolutionA cicular current loop of radius a is placed in a radial magnetic field B as shown . The net force acting of the loop is :
View SolutionIn Problem 51, what are the magnitudes of (a) the horizontal component and (b) the vertical component of the net force acting on the block at point Q ? (c) At what height h should the block be released from rest so that it is on the verge of losing contact with rest so that it is on the verge of losing contact with the track at the top of the loop ? (On the verge of losing contact means that the normal force on the block from the track has just then become zero. ) (d) Graph the magnitude of the normal force on the block at the top of the loop versus initial height h, the range h=0 to h=6R.
View Solution
