The bob of a 0.2 m pendulum describs an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is g/n. Find value of n.
1
2
3
5
The correct Answer is:1
To solve the problem step by step, we can follow these steps:
Step 1: Identify the forces acting on the bob
The forces acting on the bob of the pendulum are:
1. The weight of the bob, W=mg (acting downwards).
2. The tension in the cord, T (acting along the cord).
Step 2: Resolve the weight into components
When the pendulum makes an angle of 30∘ with the vertical, we can resolve the weight mg into two components:
- The component along the direction of the tension (vertical component):
Wvertical=mgcos(30∘)=mg⋅√32
- The component acting tangentially (horizontal component):
Wtangential=mgsin(30∘)=mg⋅12
Step 3: Set up the equation for tension
According to the problem, the tension T in the cord is given as:
T=√3⋅mg
Step 4: Apply Newton's second law in the radial direction
In the radial direction, the net force is given by:
T−Wvertical=m⋅ac
Substituting the values we have:
√3⋅mg−mg⋅√32=m⋅ac
Factoring out mg:
mg(√3−√32)=m⋅ac
This simplifies to:
mg⋅(2√32−√32)=m⋅ac
mg⋅√32=m⋅ac
Cancelling m from both sides gives:
g⋅√32=ac
Step 5: Calculate the tangential acceleration
Using Newton's second law in the tangential direction:
mgsin(30∘)=m⋅at
Substituting the values:
mg⋅12=m⋅at
Cancelling m:
g⋅12=at
Step 6: Find the net acceleration
The net acceleration a is the vector sum of the centripetal and tangential accelerations:
a=√a2c+a2t
Substituting the values:
a=
⎷(g⋅√32)2+(g⋅12)2
Calculating each term:
a=√g2⋅34+g2⋅14=√g2⋅1=g
Step 7: Relate the net acceleration to g/n
Given that the acceleration is expressed as gn:
g=gn
This implies:
n=1
Final Answer
The value of n is 1.
The forces acting on the bob of the pendulum are:
1. The weight of the bob, W=mg (acting downwards).
2. The tension in the cord, T (acting along the cord).
When the pendulum makes an angle of 30∘ with the vertical, we can resolve the weight mg into two components:
- The component along the direction of the tension (vertical component):
Wvertical=mgcos(30∘)=mg⋅√32
- The component acting tangentially (horizontal component):
Wtangential=mgsin(30∘)=mg⋅12
According to the problem, the tension T in the cord is given as:
T=√3⋅mg
In the radial direction, the net force is given by:
T−Wvertical=m⋅ac
Substituting the values we have:
√3⋅mg−mg⋅√32=m⋅ac
Factoring out mg:
mg(√3−√32)=m⋅ac
This simplifies to:
mg⋅(2√32−√32)=m⋅ac
mg⋅√32=m⋅ac
Cancelling m from both sides gives:
g⋅√32=ac
Using Newton's second law in the tangential direction:
mgsin(30∘)=m⋅at
Substituting the values:
mg⋅12=m⋅at
Cancelling m:
g⋅12=at
The net acceleration a is the vector sum of the centripetal and tangential accelerations:
a=√a2c+a2t
Substituting the values:
a=
⎷(g⋅√32)2+(g⋅12)2
Calculating each term:
a=√g2⋅34+g2⋅14=√g2⋅1=g
Given that the acceleration is expressed as gn:
g=gn
This implies:
n=1
The value of n is 1.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Check point
Explore 45 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Taking it together
Explore 67 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Matrix Matching
Explore 7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
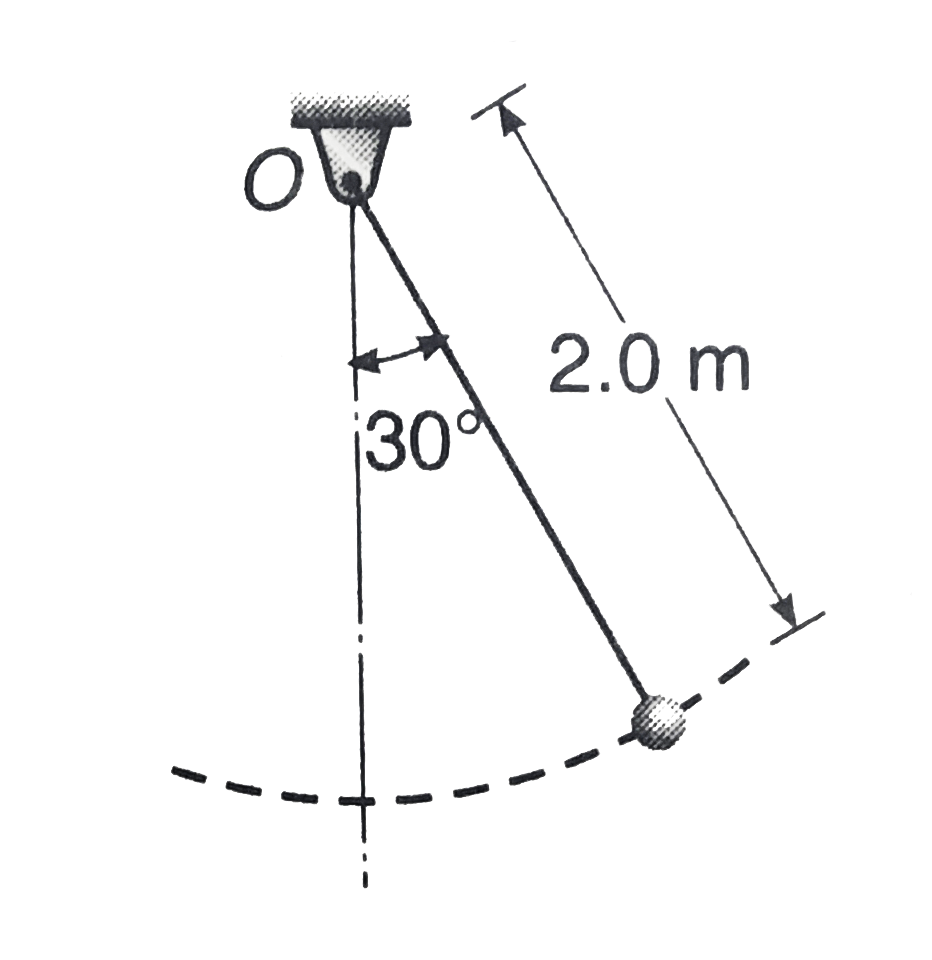
The bob of the pendulum shown in figure describes an arc of a circle in a vertical plane. If the tension in the cord is 2.5 times the weight of the bob for the position shown. Find the velocity and the acceleration of the bob in that position.
View SolutionA bob of mass m=50g is suspended form the ceiling of a trolley by a light inextensible string. If the trolley accelerates horizontally, the string makes an angle 37∘ with the vertical. Find the acceleration of the trolley.

View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
View SolutionA simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionA simple pendulum has a bob of mass m and swings with an angular amplitude ϕ. The tension in thread is T. At a certain time the string makes an angle θ with the vertical (θ≤ϕ)
View SolutionA pendulum bob has a speed of 3ms−1 at its lowest position. The pendulum is 0.5 m long. The speed of the bob, when string makes an angle of 60∘ to the vertical is (take, g=10ms−1)
View SolutionA simple pendulum suspended from the roof off a lift oscillates with frequency υ when the lift is at rest. If the lift falls freely under gravity, its frequency of oscillation becomes
View SolutionA simple pendulum of length 40 cm oscillates with an angular amplitude of 0.04 rad. Find a. the time period b. the linear amplitude of the bob, c. The speed of the bob when the string makes 0.02 rad with the vertical and d. the angular acceleration when the bob is in momentarily rest. Take g=10ms−2.
View Solution
