A particle is rotating in a cirlce of radius 1 m with constant speed 4 m/s. In time 1s, match the following (in SI unit)
Table-1Table-2(A)Displacement(P)8 sin 2(B)Distance(Q)4(C)Average velocity(R)2 sin 2(D)Average acceleration(S)4 sin 2
The correct Answer is:(A)R,(B)Q,(C)R,(D)P
To solve the problem, we will analyze the motion of a particle rotating in a circle of radius 1 m with a constant speed of 4 m/s over a time interval of 1 second. We need to find the displacement, distance, average velocity, and average acceleration, and then match them with the given options.
1. Calculate Angular Velocity (ω):
The relationship between linear velocity (v), radius (r), and angular velocity (ω) is given by:
v=r⋅ω
Given v=4m/s and r=1m:
ω=vr=41=4rad/s
Hint: Remember that angular velocity is the rate of change of angular displacement.
2. Calculate Angular Displacement (θ):
The angular displacement can be calculated using:
θ=ω⋅t
Given t=1s:
θ=4⋅1=4rad
Hint: Angular displacement is the angle through which the particle has rotated in a given time.
3. Calculate Distance Traveled:
The distance traveled by the particle along the circular path is equal to the arc length, which can be calculated as:
Distance=r⋅θ
Substituting the values:
Distance=1⋅4=4m
Hint: The distance is the length of the path traveled, which is the arc length in circular motion.
4. Calculate Displacement:
The displacement in circular motion can be found using the formula:
Displacement=2⋅r⋅sin(θ2)
Substituting the values:
Displacement=2⋅1⋅sin(42)=2⋅sin(2)=2sin(2)
Hint: Displacement is the straight-line distance from the starting point to the endpoint.
5. Calculate Average Velocity:
Average velocity is defined as:
Average Velocity=Displacementt
Substituting the values:
Average Velocity=2sin(2)1=2sin(2)m/s
Hint: Average velocity considers the straight-line displacement over time.
6. Calculate Average Acceleration:
Average acceleration can be calculated as:
Average Acceleration=Change in Velocityt
In circular motion, the change in velocity can be related to the average velocity:
Average Acceleration=2⋅2sin(2)1=4sin(2)m/s2
Hint: Average acceleration is the change in velocity over the time interval.
Matching Results with Options:
- (A) Displacement → (R) 2sin2
- (B) Distance → (Q) 4
- (C) Average Velocity → (R) 2sin2
- (D) Average Acceleration → (S) 4sin2
Final Matching:
- (A) Displacement → (R) 2sin2
- (B) Distance → (Q) 4
- (C) Average Velocity → (R) 2sin2
- (D) Average Acceleration → (S) 4sin2
The relationship between linear velocity (v), radius (r), and angular velocity (ω) is given by:
v=r⋅ω
Given v=4m/s and r=1m:
ω=vr=41=4rad/s
The angular displacement can be calculated using:
θ=ω⋅t
Given t=1s:
θ=4⋅1=4rad
The distance traveled by the particle along the circular path is equal to the arc length, which can be calculated as:
Distance=r⋅θ
Substituting the values:
Distance=1⋅4=4m
The displacement in circular motion can be found using the formula:
Displacement=2⋅r⋅sin(θ2)
Substituting the values:
Displacement=2⋅1⋅sin(42)=2⋅sin(2)=2sin(2)
Average velocity is defined as:
Average Velocity=Displacementt
Substituting the values:
Average Velocity=2sin(2)1=2sin(2)m/s
Average acceleration can be calculated as:
Average Acceleration=Change in Velocityt
In circular motion, the change in velocity can be related to the average velocity:
Average Acceleration=2⋅2sin(2)1=4sin(2)m/s2
- (A) Displacement → (R) 2sin2
- (B) Distance → (Q) 4
- (C) Average Velocity → (R) 2sin2
- (D) Average Acceleration → (S) 4sin2
- (A) Displacement → (R) 2sin2
- (B) Distance → (Q) 4
- (C) Average Velocity → (R) 2sin2
- (D) Average Acceleration → (S) 4sin2
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Integer
7 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Check point
45 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Comprehension
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A particle is revolving in a circular path of radius 2 m with constant angular speed 4 rad/s. The angular acceleration of particle is
View SolutionA particle moves in a circle of radius R=2122m with constant speed 1m/s. Find,
(a) magnitude of average velocity and
(b) magnitude of average acceleration in 2 s.
View SolutionMatch the following.
∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣Table-1Table-2(A)Coefficient of viscosity(P)[M2L−1T−2](B)Surface tension(Q)[ML0T−2](C)Modulus of elasticity(R)[ML−1T−2](D)Energy per unit volume(S)Noneof a fiuid∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionA particle is moving on a circular path of radius 1 m with 2 m/s. If speed starts increasing at a rate of 2m/s2, then acceleration of particle is
View SolutionMatch the following
Table - 1Table - 2(A)σ2/ε0(P)C2/J−m(B)ε0(Q)Farad(C)ampere - secondVolt(R)J/m3(D)VE(S)metre
View SolutionMatch the following
∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣Table-1Table-2(A)Stress×Strain(P)J(B)YAl(Q)N/m(C)Yl3(R)J/m3(D)FlAY(S)m∣∣ ∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionA particle is moving with speed v=2t2 on the circumference of a circle of radius R. Match the quantities given in Table-1 with corresponding results in Table-2
Table-1Table-2(A)Magnitude to tangential acceleration of particle(P)decreases with time(B)Magnitude of centripetal acceleration of particle(Q)increases with time(C)Magnitude of angular speed of particle with respect to centre of circle(R)remains constant(D)Angle between the total acceleration and centripetal acceleration of partilce(S)depends upon the value of radius R
View SolutionMatch the following
Table-1Table-2(A)L(P)[M0L0T−2](B)Magnetic Flux(Q)[ML2T−2A−1](C)LC(R)[ML2T−2A−2](D)CR2(S)None
View SolutionFor the velocity -time graph shown in figure, in a time interval from t=0 to t=6s, match the following:
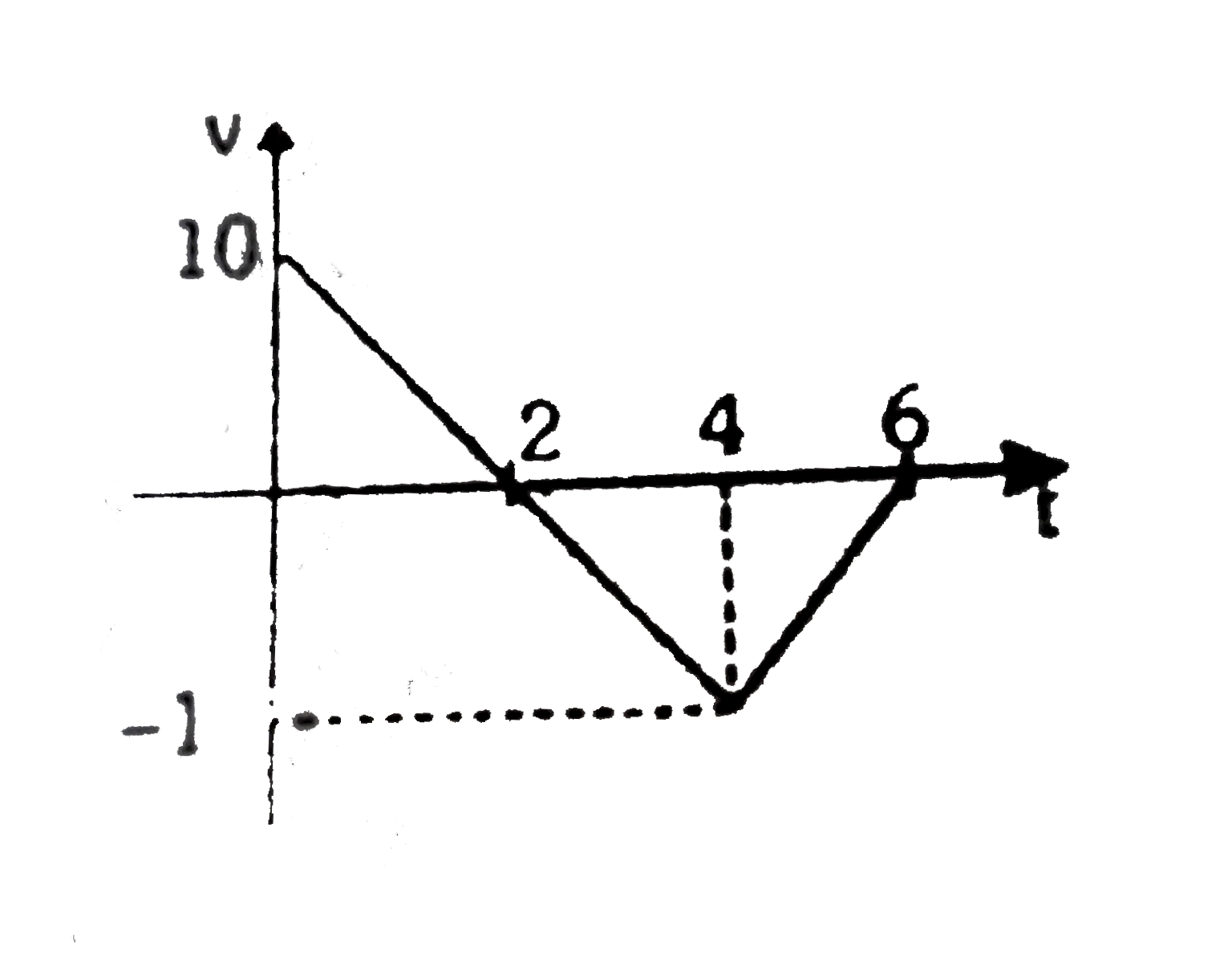
Column IColumn II(A)Change in velocity(p)−5/3SIunit(B)Average acceleration(q)−20SIunit(C)Total displacement(r)−10SIunit(D)Acceleration ay t=3s(s)−5SIunit
View SolutionA particle is moving in a circel of radius R=1m with constant speed v=4m/s. The ratio of the displacement to acceleration of the foot of the perpendicular drawn from the particle onto the diameter of the circel is
View Solution
