The bob of a pendulum at rest is given a sharp hit to impart a horizontal velocity $\sqrt{10 g l}$ where l is the length of the pendulum. Find the tension in the string when a. the string is horizontal. B. The bob is at its highest point and c. the string makes an angle of $60^{0}$ with the upward vertical.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C

a.Let the velocity at B be $v_{2}$
$\frac{1}{2} m v_{1}^{2} = \frac{1}{2} m v_{2}^{2} + m g l$
$\to \frac{1}{2} m (10 g l) = \frac{1}{2} m v_{2}^{2} + m g l$
$v_{2}^{2} = 8 g l$

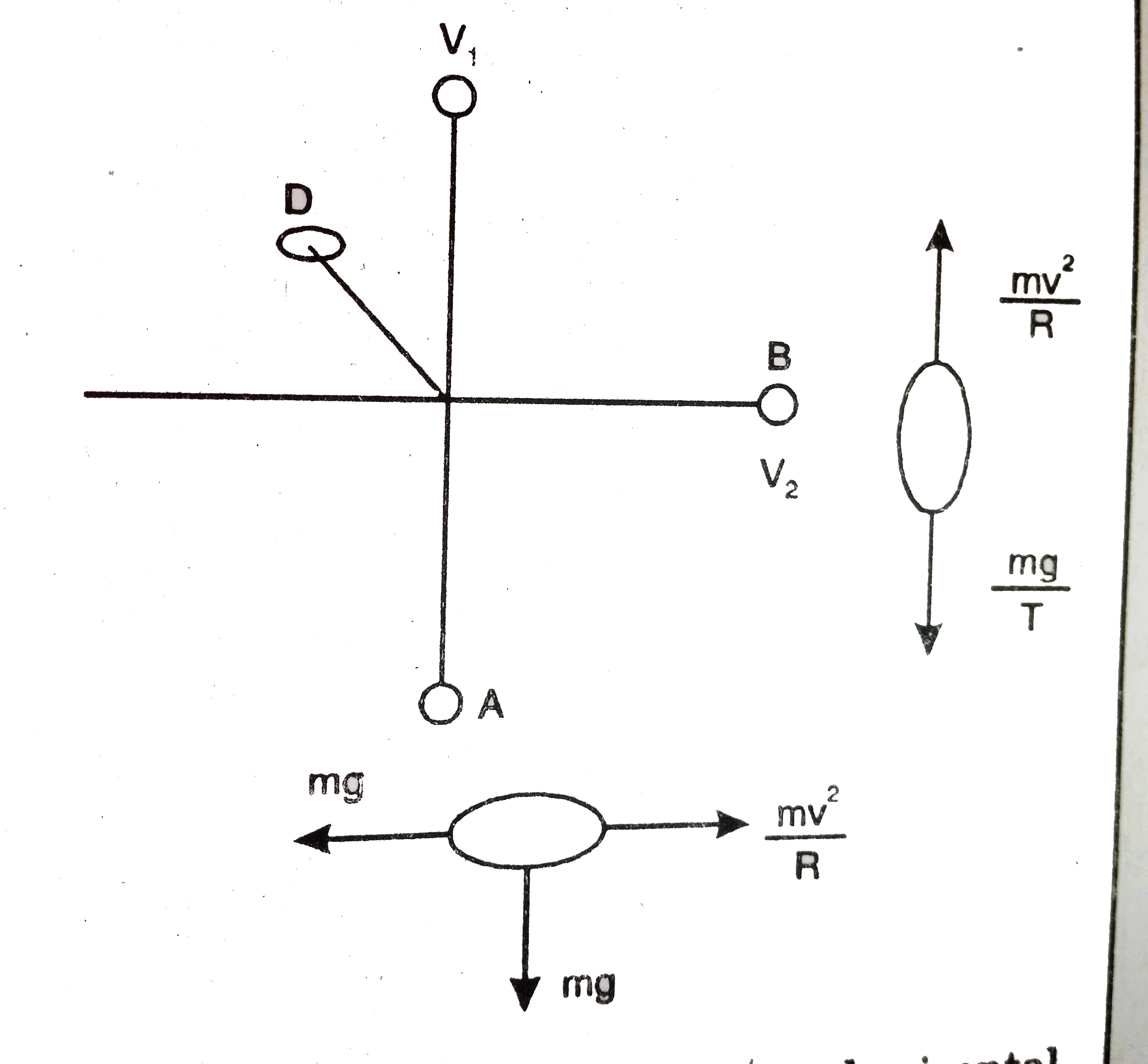
so the tension in the string at horizontal position
$T = \frac{m v^{2}}{R} = m \frac{8 g l}{l}$
$= 8 m g$
b. Let the velocity at C be $v_{3}$
$\frac{1}{2} m v_{1}^{2} = \frac{1}{2} m v_{3}^{2} + m g 2 l$
$\to \frac{1}{2} m 10 g l = \frac{1}{2} m v_{3}^{2} + 2 m g l$
$\to v_{3}^{2} = 6 g l$
So, the tension in the string is given by
$T_{C} = \frac{m v_{3}^{2}}{l} - m g = 5 m g$
c. Let the velocity at point D be $v_{4} < b r > A g a \in$ 1/2 mv_1^2=1/2 mv_4^2+mgl(1+cos60^0) $< b r >$ rarr v_4^2=7gl $< b r > s o, t h e t e n s i o n \in t h e s t r \in g i s < b r >$ T_D=(mv^2)/l-mgcos 60^0 $< b r >$ =m(7gl)/l-0.5 mg $< b r >$ =7mg=0.5mg $< b r >$ 6.5 mg

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

HC VERMA ENGLISH-WORK AND ENERGY-Exercises

Home
Ask Doubt
Profile